Kolik stran má kruh?

Jedná se o domácí úkol ze základní školy, který vyvolává neshody mezi zkušenými matematiky. Abych zjistil správnou odpověď, použil jsem ten nejpřísnější vědecký nástroj, anketu na Twitteru:

Zpětně lituji, že jsem nezahrnul možnost „žádný z výše uvedených“, ale o tom později. V tomto příspěvku projdu tyto tři odpovědi (a „žádná z výše uvedených“) a proberu jejich klady a zápory, jak je vidím já, než dramaticky odhalím správnou odpověď.

Ale nejprve: proč nemůžeme rovnou uvést správnou odpověď? Slova v otázce jsou sotva záhadná. Všichni víme, co je to „kruh“, co znamená počítat „kolik“ něčeho a co je to „strana“… nebo ne? Zde jsou (hrubé) definice, které jsem vydestiloval z diskuse se dvěma žáky základní školy, kteří se ocitli na konci této otázky:

1. Jaký je počet kruhů? Čára tvořící část hranice tvaru rovinného útvaru.

Účelem toho, že zde říkáme rovinný útvar místo „tvar“, je, že chceme tvary, které žijí ve dvou rozměrech (např. čtverce nebo kruhy, ale ne koule nebo krychle). Další otázkou je, co je to „čára“ v definici 1. Zde je varianta, která to upřesňuje:

2. Přímka tvořící část hranice rovinného útvaru.

Pokud zadáte do Googlu „define: side“, nejrelevantnější definice je:

Přímkový útvar je útvar sestrojený z přímek. Tato definice je tedy dalším zpřesněním definice 2 a umožňuje nám potvrdit, že čtverec má čtyři strany, ale na první pohled nemá co říci o nerektilineárních rovinných útvarech, jako jsou kružnice.

Konečně mnoho stran?

Myslím, že je jisté, že respondenti mé ankety na Twitteru mají vyšší úroveň matematického vzdělání, než je celostátní průměr. Skutečnost, že se v této otázce vůbec rozdělili a že malá většina zvolila odpověď, která je pro obvyklé publikum této otázky (žáky základních škol) dost dobře nedostupná, rozhodně naznačuje, že někde není něco v pořádku.

Takže, má kruh nekonečně mnoho stran? Rozhodně je užitečné uvažovat o kruhu jako o limitu n-úhelníků s tím, že n je stále větší a větší. Přesně tento přístup používali Archimédes, Liou Chuej a nespočet dalších v průběhu staletí při studiu kruhové geometrie, včetně toho, že přišli s aproximacemi pro π.

Vydání knihy Jiuzhang suanshu (Devět kapitol o matematickém umění) z 16. století za dynastie Ming, třetí století našeho letopočtu.

Někdy je naprosto rozumné jako pohodlnou zkratku uvažovat o kruhu jako o mnohoúhelníku s nekonečně mnoha stranami.

Ale jako nesnesitelný pedant matematik bych chtěl rozlišovat mezi pohodlnou zkratkou a doslovnou pravdou. Jsme-li neoblomní v tom, že kruh je skutečně mnohoúhelník s nekonečně mnoha stranami, pak se nabízí otázka: Jaké jsou ty strany? A jistě jediná věrohodná odpověď zní: jednotlivé body kruhu. Jak dlouhé jsou tyto takzvané strany? Nula centimetrů. A jsou tyto strany odděleny rohy? Zřejmě ne, buď vůbec žádné rohy nejsou, nebo je každý bod zároveň stranou i rohem.

Řekl bych, že strany o délce nula jsou… problematický pojem. Jak poznáš, jestli nějaké máš? Předpokládejme například, že studuji soustavu, kde čtverec vzniká jako limita osmiúhelníků takto:

V této situaci by pro mě mohlo mít smysl uvažovat o svém čtverci jako o čtverci s osmi stranami, z nichž čtyři mají délku nula. Kdybych však trval na tom, že můj (naprosto obyčejný) čtverec má skutečně osm stran, možná byste pozvedli obočí.

Takže tato – vítězná odpověď v mé anketě – je jediná, kterou prohlásím za definitivně chybnou, a zároveň je to jediná odpověď, která vůbec nabízí nějaký geometrický vhled. Paradox? Ani ne. Uvažování pomocí analogie je v matematice i v životě cenná dovednost; zároveň je důležité udržet si vědomí, že právě to děláme.

Pro nekonečně mnoho stran: geometricky poučné.
Proti nekonečně mnoha stranám: osmistěnné čtverce.

Na tangentě 1: apeirogony

I když kruh není, existují takové věci jako mnohoúhelníky s nekonečně mnoha stranami? No, pro popis takové věci existuje slovo apeirogon. Pravidelný apeirogon by pak měl strany stejné (nenulové) délky a mezi nimi stejné úhly. Jedinou možností je zde tento hloupě nezajímavý objekt:

Pokud máte námitky, že se jedná o „mnohoúhelník“ (buď bkvůli úhlům 180°, nebo řetězci hran neuzavírajícímu se do smyčky), co třeba něco takového: Začněte ve spodní části kruhu a v každé fázi se pohybujte po polovině toho, co z kruhu zbývá, a oblouk, který jste právě urazili, nahraďte přímkou:

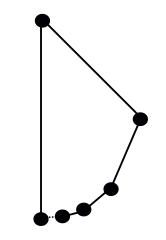
Je to skutečný mnohoúhelník? Opět záleží na vašich podmínkách. Podle jedné z běžných definic, totiž definice „uzavřeného mnohoúhelníkového řetězce“, toto nesplňuje podmínky, protože počáteční roh (vlevo dole) navazuje pouze na jednu hranu. Ale je to velmi blízko: tento bod je hranicí posloupnosti hran zprava, což z tohoto útvaru dělá „nesamostatně se protínající kusovou lineární uzavřenou křivku“, což je další definice mnohoúhelníku, kterou lidé používají.

Pokud opustíme náš obvyklý euklidovský svět a vstoupíme do hyperbolického prostoru, pak zde není žádná dvojznačnost. Apeirogony (dokonce pravidelné apeirogony) prostě existují:

Kachle hyperbolické roviny pravidelnými apeirogony. (Autor: Anton Sherwood – vlastní dílo, Public Domain, https://commons.wikimedia.org/w/index.php?curid=13260274 )

Na tečně 2: krajní body

Možná by bylo obhajitelnější říci, že kružnice má nekonečně mnoho rohů než nekonečně mnoho stran (i když se zdá, že tato otázka není kladena příliš často). Začněme tím, že pokud je roh čtverce bod, v němž jeho hraniční čára není přímá, pak to splňuje každý bod na kružnici. Složitější je pojem krajního bodu útvaru: je to každý bod, kterým lze protáhnout úsečku přímky, která se dotýká útvaru právě jen v tomto bodě. U čtverce a mnoha známých tvarů se krajní body přesně shodují s rohy. Každý bod na hranici kružnice je krajním bodem, takže určitě platí, že kružnice jich má nekonečně mnoho.

Mohli bychom se obávat, že některé útvary, jako je tento chevron, mají rohy, které nejsou krajními body:

Zde spodní střední roh není krajním bodem (ostatní tři rohy ano). Co je špatně, je to, že tento tvar není konvexní (zhruba má některé kousky vyčnívající příliš daleko). Kruh je konvexní, takže si snad nemusíme dělat starosti. Případně bychom mohli situaci napravit tím, že definujeme „roh“ jako bod, který je krajním bodem buď daného tvaru, nebo jeho doplňku, tj. celé roviny s vyříznutým tvarem. Tento přístup by umožnil detekovat rohy všech mnohoúhelníků, včetně chevronu. U hladkých křivek by jako „rohy“ identifikoval všechny hraniční body s výjimkou inflexních bodů (což není nerozumné, protože bychom mohli tvrdit, že tam je hranice přímá).“

Jedna strana?

Na základní škole se zdá, že odpověď „jedna“ je ta, která dostane zaškrtnutí. A existuje k tomu středně slušné zdůvodnění. Vzpomeňte si na výše uvedenou definici 1:

1. Přímka tvořící část hranice rovinného útvaru.

Bezprostřední otázkou je, co se počítá za „přímku“, zejména pokud netrváme na přímosti. Jsme-li v tomto ohledu příliš uvolnění, pak by se o každém rovinném útvaru dalo říci, že má „jednu stranu“ ve stejném smyslu, jako má jednu hranici, obvod nebo obvod. To však musí být špatně, protože jistě chceme, aby čtverec měl čtyři. No, čtverec má čtyři body, kde není hladký, a čtyři hladké úseky mezi nimi. Možná jsme celou dobu počítali skutečně s hladkými úseky. Implicitně tedy máme nové zpřesnění definice 1 (a také využíváme příležitosti zbavit se vágního termínu „figura“):

4. Každý hladký úsek kusově hladké uzavřené křivky.

„Uzavřená křivka“ je taková, která se smyčkou setkává sama se sebou, takže nemá žádné volné konce. „Kusově hladká“ znamená, že je sestavena z hladkých úseků, které se setkávají v izolovaných nehladkých bodech. Je zcela legitimní chtít počítat hladké úseky hranice takového útvaru a v žádném případě není pobuřující používat při tom slovo „strana“. Rozhodně tedy netvrdím, že je to definitivně špatná odpověď.

Jde o to, zda je taková interpretace slova „strana“ nejen koherentní, ale i natolik přirozená, že ji lze jednoduše předpokládat, aniž by byla explicitně uvedena (což se děje zřídka, pokud vůbec). Co se stane, když se hladkost a přímost shodují různě? Uvažujme tento tvar náhrobku, který vznikl nahrazením vrcholu čtverce půlkruhem o stejném průměru.

Ten má dvě hladké části (spodní čáru a zbytek), ale tři rovné hrany (plus zakřivený kus hladce spojující dvě z nich). Kolik má tedy stran? Znovu jsem se poradil se svými přáteli na Twitteru:

Tentokrát jsem měl jako možnost uvést „nekonečně mnoho“, i když to se dá vstřebat do „nic z výše uvedeného“. Každý, kdo hlasuje, že kruh má nekonečně mnoho stran, by zde měl automaticky hlasovat pro „Žádnou z výše uvedených možností“, pokud – což je důležitá výhrada – povaha tohoto tvaru čtenáři nenaznačuje jiné pojetí „strany“. Skutečnost, že nejoblíbenější volby v těchto dvou anketách jsou neslučitelné, naznačuje, že tomu tak může být (nebo přinejmenším posiluje, že vody jsou kalné).

Ačkoli je dvojka naprosto slušná odpověď, slučitelná s výše uvedenou definicí 4 a s jednostranností kruhu, nejsem přesvědčen, že je definitivně správná, nebo že trojka či čtyřka jsou kategoricky špatné. Záleží na tom, co chcete počítat: hladké výseče, rovné hrany nebo rovné hrany plus to, co pak zbude, přičemž kterákoli z těchto možností může být požadovanou odpovědí v závislosti na kontextu (více o tom níže). S tím souvisí, že si nejsem jistý, zda počítání počtu hladkých úseků plně odpovídá mé intuici slova „strana“. Koneckonců dvě svislé části náhrobku jsou – myslím, že je spravedlivé říci – „na opačných stranách“. Opravdu se spokojíme s tím, že jsou současně součástí „téže strany“?“

Možná namítnete, že směšuji dva různé významy slova „strana“, že terminologie se někdy střetává a my s tím prostě musíme žít. Já si tím však nejsem tak jistý. Smyslem tohoto cvičení je extrapolovat ze situace (přímočaré útvary), kde se oba pojmy docela dobře shodují. Pokud by existovala nová myšlenka, která by zachycovala vše, co se nám líbilo na té původní, ale zároveň by se vztahovala na širší kategorii útvarů, pak by měla drtivý nárok na to být tou jedinou správnou odpovědí. Pokud však všechny naše pokusy o zobecnění zahrnují obětování žádoucích aspektů originálu, pak možná neexistuje jediné správné zobecnění. Existují různé možnosti s různými kompromisy, které mohou být vhodné v různých kontextech (a pokud jsme v situaci, kdy je ve hře více než jedna, pak by bylo užitečné jim dát různá jména).

Tady je další varianta: Weierstrassův náhrobek vytvořený nahrazením horní hrany čtverce řezem Weiestressovy funkce, nekonečně klikatou čarou, která není nikde hladká.

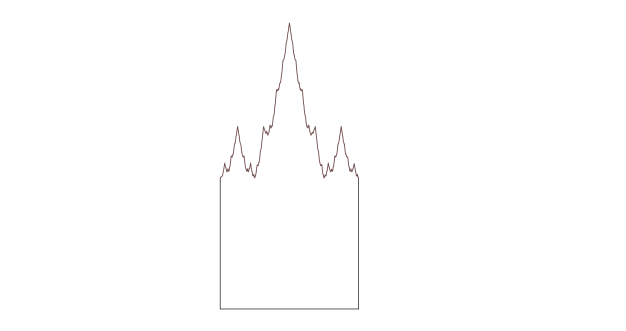
Tady je (a všimněte si překlepu), co z toho udělali moji přátelé na Twitteru – i když méně z nich se odvážilo vyjádřit svůj názor:

Nehledě na skepsi mých příznivců na Twitteru za chvíli vysvětlím, proč si nemyslím, že je hloupé vidět, že to má čtyři strany (z nichž jedna není hladká). Na druhou stranu, pokud dáváte přednost hladkým stranám, pak máte opět na výběr mezi tím, zda to vidíte tak, že to má nekonečně mnoho stran (z nichž tři mají délku 1 a zbytek má délku 0), nebo tak, že to má tři strany plus úsek rozhodně-ne-hranice.

Pro jednu stranu: jediná hladká křivka.
Pro jednu stranu: stejná strana na protilehlých stranách.

Na tečně 3: strany versus hrany

Kolik stran má čtverec? Čtyři. Kolik má hran? Čtyři. Jsou tedy hrany a strany totéž? Ne nutně. Zde jsou dvě konfigurace, které jsou – alespoň pravděpodobně – každá čtyřstranná, ale mají 5, respektive 3 hrany:

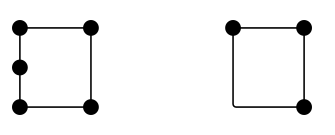
Obvykle bych řekl, že „hrana“ je topologický objekt v tom smyslu, že důležitá je její funkce, nikoli tvar. Vzpomeňte si na mapu londýnského metra. Kdybyste se zeptali, kolik je v té síti hran, nemělo by smysl sčítat rovné nebo hladké úseky. Počítají se spojení mezi stanicemi (nebo vrcholy).

Jak již bylo řečeno, je běžné si mnohoúhelník představit jako velmi jednoduchý druh sítě, kterému se říká uzavřený mnohoúhelníkový řetězec: řetězec vrcholů (v tomto případě rohů mnohoúhelníku), propojených hranami tak, že každý vrchol leží přesně na dvou hranách a celek tvoří jedinou smyčku. V této situaci se hrany a strany shodují, stejně jako vrcholy a rohy. Obecně však můžete tuto shodu porušit, jako ve dvou malých sítích výše.

Pokud chcete o věcech uvažovat síťově-teoreticky, ale vrcholy nejsou jasně označeny, pak musíte hádat, kde jsou. U mnohoúhelníku je to snadné – vrcholy jsou v rozích – proto je přepínání mezi geometrickým a topologickým přístupem tak přirozené. U jiných tvarů, jako je například některý z výše uvedených náhrobků, to však nemusí být tak zřejmé. Nicméně v každém případě, kdyby vám někdo řekl, že tam někde jsou vrcholy, a požádal vás, abyste je našli, myslím, že by bylo rozumné odhadnout, že jsou čtyři, konkrétně rohy původního čtverce, a že horní hrana byla z nějakého důvodu znázorněna jako nerovná čára. A pokud bychom skutečně chtěli uvažovat tímto způsobem, že každý z náhrobků má čtyři hrany, pak by to mohlo působit převráceně (i když logicky koherentně!) trvat na tom, že mají nějaký jiný počet stran (zejména proto, že horní strana je – navzdory své geometrii – jasně „na jedné straně“ obrázku). Ve skutečnosti se mě jeden z mých korespondentů na Twitteru místo hádání zeptal: „Byly odstraněny oba horní vrcholy?“, což je otázka, která dává smysl pouze z hlediska teorie sítí.

Kde tedy zůstává kruh? Potíž je v tom, že žádný bod na kruhu nemá větší nárok být vrcholem než kterýkoli jiný. Ačkoli je tedy lákavé (a opět koherentní) nahlížet na kružnici jako na síť s jednou hranou, pokud do ní budeme vkládat vrcholy, není žádný zřejmý důvod upřednostňovat jedno číslo před jakýmkoli jiným.

Mohli bychom na ni nahlížet jako na síť, která nemá vůbec žádné vrcholy, jakousi linku metra bez stanic? Obvyklé matematické pojetí sítě by to neumožňovalo, ale to by nás nemělo příliš odradit. To naznačuje čistě topologický přístup. Potíž je v tom, že z tohoto pohledu sice může být kružnice druhem sítě bez vrcholů a s jednou hranou, ale stejně tak i čtverec (pokud je tak náhodou rozvržena linka metra). V topologii je čtverec kružnicí. (To není paradox, jen se tím říká, že hranicí je jediná smyčka, na jejímž tvaru nezáleží). Takže zatímco tento druh sítě má „jednu hranu“, čtverec zjevně nemá „jednu stranu“, takže vztah mezi stranami (geometrickými) a hranami (topologickými) se opět rozpadl, stejně jako ve dvou malých sítích zobrazených výše. Tento přístup nás tedy příliš daleko dopředu neposune.

No Sides?

Může se zdát paradoxní tvrdit, že kruh (nebo jakýkoli jiný tvar) nemá „žádné strany“. Argument na obhajobu je však přímočarý. Vrátíme se k definici 2:

2. Přímka tvořící část hranice rovinného útvaru.

Jedná se o jednoduchou, snadno pochopitelnou větu, která dokonale vystihuje strany čtverce. Nepodařilo se nám najít její uspokojivé zobecnění na zakřivené útvary, proto je nejlepší zůstat u originálu. A kruh žádné nemá.

Pro žádné strany: pravda, podle rozumného pojetí „strany“.
Pro žádné strany: zní to jako zenový kóan.

Nic z výše uvedeného?

Připomeňme si definici dodanou Googlem:

3. Každá z přímek tvořících hranici rovinného rektilineárního útvaru.

Pokus o aplikaci na kruh – nerektilineární útvar – nevede k ničemu. Otázka je stejně nesmyslná jako „Kolik stran má pondělí?“

Protože definice 3 je nejoptimálnější (jediná v tomto příspěvku, kterou jsem si nevymyslel já nebo moje děti), neznamená to, že „žádná z výše uvedených“ je kategoricky správná odpověď? Možná. Na druhou stranu: když nám někdo položí otázku, princip dobročinnosti snad vyžaduje, abychom předpokládali, že je smysluplná, pokud nemůžeme pevně stanovit opak, a definice 1, 2, 4 a další varianty to umožňují. Navíc definice 3 je spíše lingvistická než formálně matematická, a je tedy spíše deskriptivní než preskriptivní, takže bychom se podle ní neměli skrývat.

Pro nic z výše uvedeného: sémantická porucha.
Pro nic z výše uvedeného: dialogická charita.

Správná odpověď

Co mě přimělo napsat tento příspěvek? Stejně jako nespočet žáků základních škol, i moje pětiletá dvojčata – žáci základní školy zmínění na začátku – dostala nedávno v domácím úkolu tuto otázku. Jeden se přiklonil k variantě „1“ a druhý k variantě „0“ a já jsem se výše pokusil zachytit a rozvinout jejich úvahy. Myslím, že obě odpovědi jsou zcela obhajitelné – a ani jedna není definitivně správná.

Takže, co byste měli dělat, když vám někdo položí tuto otázku: Kolik stran má kruh? Podle mého názoru je optimální odpovědí oslovit matematika ve svém životě, aby na toto téma napsal pojednání o 3000 slovech, které pak můžete vytisknout a vítězoslavně předat svému nešťastnému učiteli. Pokud se vám to však nepodaří, je nejlepším přístupem následovat Sokratův příklad a odpovědět na otázku protiotázkou:

Když je vše řečeno a uděláno, počítání do nuly nebo do jedné nebo odmítnutí odpovědět na otázku nám o geometrii kruhů neřekne prakticky nic. Můžeme však hodně získat tím, že rozebereme známé pojmy, vypustíme nebo přidáme další podmínky, zpochybníme svou intuici tím, že přejdeme z jednoho kontextu do trochu jiného, a pokusíme se přesně zapsat, co myslíme konkrétním pojmem v konkrétním prostředí. O tom je skutečná matematika.

Poznámky pod čarou

Mohli byste udělat něco jiného: např. zvolit si na kružnici výchozí bod P, od kterého budete měřit vzdálenost po obvodu. Pak prohlaste, že body v racionální vzdálenosti od P jsou rohy a zbytek jsou strany. To má za následek, že získáme spočetně nekonečný počet rohů a nespočetně nekonečný počet stran. Nebo lze stanovit opak. To by se mohlo hodit pro polygonální limitní přístup ke kružnicím, ale těžko bych souhlasil s tím, že je to dostatečně snadné nebo zřejmé, aby se to dalo považovat za „správnou odpověď“.

Jeden z mých korespondentů na Twitteru se obával, jak je křivka hladká. Tento náhrobek je spojitě diferencovatelný, ale ne dvakrát. Bylo by jistě zajímavé, kdyby si mnoho lidí myslelo, že je to kritická záležitost, a pravděpodobně by se to dalo otestovat pomocí nekonečně hladkého náhrobního kamene sestaveného z něčeho takového, i když jsem nedomyslel detaily.

Mohli bychom to zkusit formalizovat takto: Ve čtverci (nebo jakémkoli mnohoúhelníku) má strana tu vlastnost, že počínaje libovolným místem uvnitř můžete útvar protnout přímo skrz své místo tak, že vámi zvolená strana je pevně na jedné straně řezu. To u dvoustranného náhrobku nefunguje: jakýkoli řez vždy odřízne delší stranu. Mohli bychom to oslabit tím, že abychom mohli počítat jako stranu, musí existovat alespoň jeden způsob, jak tvar proříznout tak, aby strana byla na jedné straně řezu. To by nám umožnilo říci, že náhrobek má čtyři strany (i když zakřivený řez není na jedné straně bodů v horní oblasti). U kruhu však jeho předpokládaná jedna strana nikdy není na jedné straně (takže by byla vyloučena) a jako strana by se počítal pouze rovný řez půlkruhu.

Není snadné vymyslet rigorózní zdůvodnění, které by fungovalo pro oba náhrobky, ale neformálněji uvažuji o Schellingových bodech: tedy o místech, která vyčnívají jako zvláštní z důvodů, které nemusí být snadné předem předvídat.

Poděkování

Děkuji všem, kteří se zúčastnili mé ankety nebo ji přeposlali, případně se mnou diskutovali na Twitteru.