Předpoklad – Základy teorie grafů – sada 1
Graf je struktura představující množinu objektů, ve které jsou některé dvojice objektů v určitém smyslu „příbuzné“. Objekty grafu odpovídají vrcholům a vztahy mezi nimi hranám. Graf se schematicky znázorňuje jako množina bodů znázorňujících vrcholy spojené čarami nebo křivkami znázorňujícími hrany.
Formálně,
„Graf 
se skládá z 
, neprázdné množiny vrcholů (nebo uzlů) a 
, množiny hran. Každá hrana má buď jeden, nebo dva vrcholy, které jsou s ní spojeny a nazývají se její koncové body.“
Typy grafů :Existuje několik typů grafů rozlišovaných na základě hran, jejich směru, váhy atd.
1. Jednoduchý graf – Graf, ve kterém každá hrana spojuje dva různé vrcholy a kde žádné dvě hrany nespojují stejnou dvojici vrcholů, se nazývá jednoduchý graf. Uvažujme například následující graf –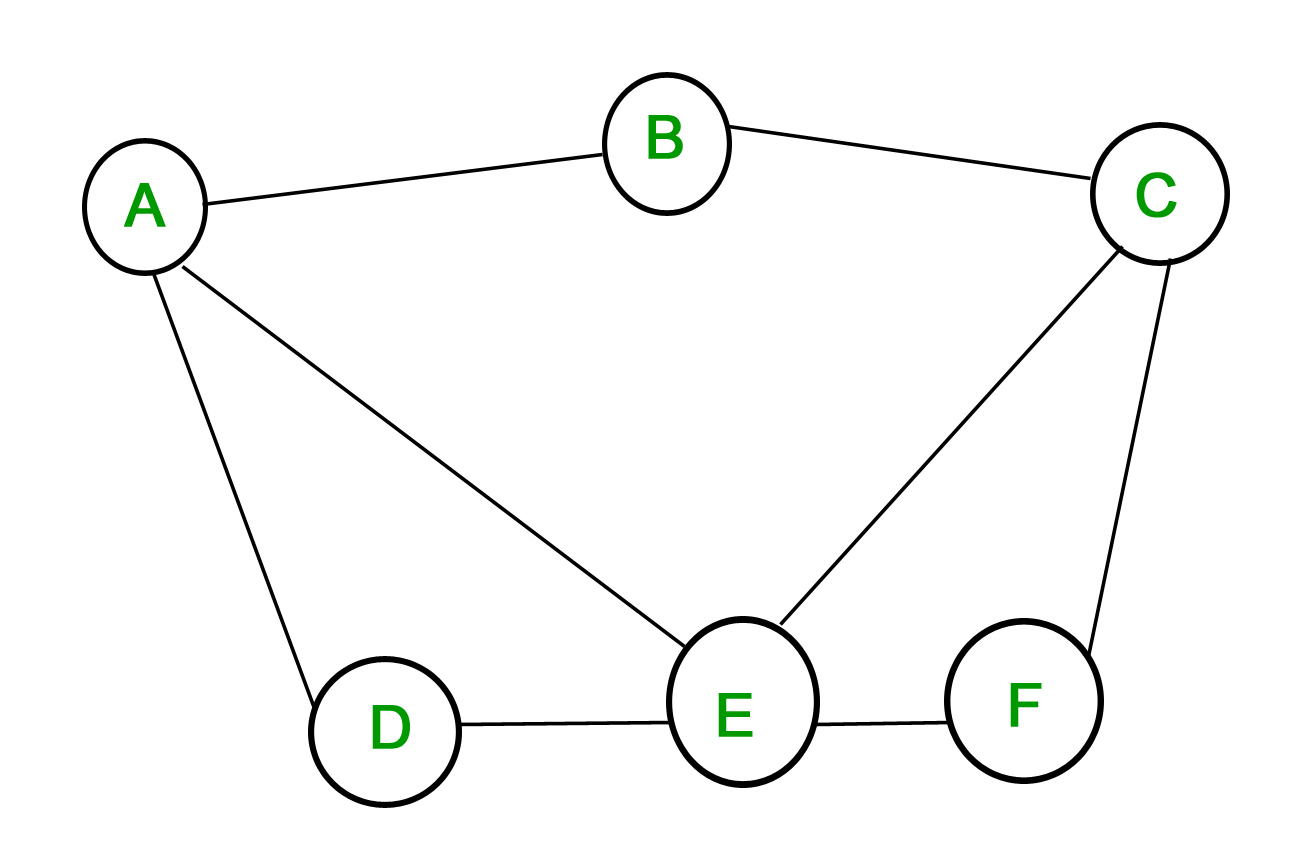
Výše uvedený graf je jednoduchý graf, protože žádný vrchol nemá vlastní smyčku a žádné dva vrcholy nemají více než jednu hranu, která by je spojovala.
Hrany jsou označeny vrcholy, které spojují – 
je hrana spojující vrcholy 
a 
.
2. Graf je jednoduchý. Multigraf – Graf, ve kterém může stejnou dvojici vrcholů spojovat více hran, se nazývá multigraf.
Protože mezi stejnou dvojicí vrcholů může být více hran, udává násobnost hran počet hran mezi dvěma vrcholy.
Výše uvedený graf je multigraf, protože mezi a 
je více hran. Násobnost hrany 
je 2.
V některých grafech, na rozdíl od výše uvedeného, jsou hrany směrované. To znamená, že vztah mezi objekty je pouze jednosměrný, nikoliv obousměrný. Směrovost hran může být v některých aplikacích důležitá.
Na základě toho, zda jsou hrany směrované nebo ne, můžeme mít směrované grafy a nesměrované grafy. Tuto vlastnost lze rozšířit na jednoduché grafy a multigrafy a získat tak jednoduché směrované nebo nesměrované jednoduché grafy a směrované nebo nesměrované multigrafy.
Základní terminologie grafů :
V předchozím pojednání již byly vysvětleny některé pojmy týkající se grafů, jako jsou vrcholy, hrany, směrované a nesměrované hrany atd. Existují i další termíny, které popisují vlastnosti vrcholů a hran.
- Přilehlost – V grafu
se říká, že dva vrcholy 
a 
spolu sousedí, jestliže jsou koncovými body hrany. Říká se, že hrana 
je s vrcholy incidentní.
V případě, že je hrana směrovaná, říká se, že sousedí s a sousedí z . Zde se říká, že je intitiální vrchol a je koncový vrchol. - Stupeň – Stupeň vrcholu je počet hran, které s ním incidentují, s výjimkou vlastní smyčky, která ke stupni vrcholu přispívá dvakrát. Stupeň vrcholu se označuje jako
.
V případě směrovaných grafů se stupeň dále klasifikuje jako in-stupeň a out-stupeň. In-stupeň vrcholu je počet hran s daným vrcholem jako koncovým vrcholem. Out-stupeň vrcholu je počet hran s daným vrcholem jako počátečním vrcholem. In-stupeň se značí jako
a out-stupeň se značí jako 
.
Například ve výše uvedeném směrovaném grafu znázorňujícím lety mezi městy je in-stupeň vrcholu „Dillí“ 3 a jeho out-stupeň je také 3.
Poznámka: Pokud má vrchol nulový stupeň, nazývá se izolovaný. Pokud má stupeň jedna, pak se nazývá přívěsek.
Věta o ruce :
Co bychom dostali, kdybychom sečetli stupně všech vrcholů grafu. V případě neorientovaného grafu přispívá každá hrana dvakrát, jednou za svůj počáteční vrchol a podruhé za svůj koncový vrchol. Součet stupňů je tedy roven dvojnásobku počtu hran. Tato skutečnost je uvedena ve větě o podávání rukou.
Let be an undirected graph with edges. ThenIn case G is a directed graph,
Věta o podávání rukou má pro neorientované grafy zajímavý výsledek –
An undirected graph has an even number of vertices of odd degree.
Důkaz : Nechť 
a 
jsou množiny vrcholů sudých, resp. lichých stupňů.
Víme z věty o podávání rukou, že,
Takže,
Součet stupňů vrcholů se sudými stupni je sudý. LHS je také sudá, což znamená, že součet stupňů vrcholů s lichými stupni musí být sudý.
Takže počet vrcholů s lichými stupni je sudý.
Některé speciální jednoduché grafy :
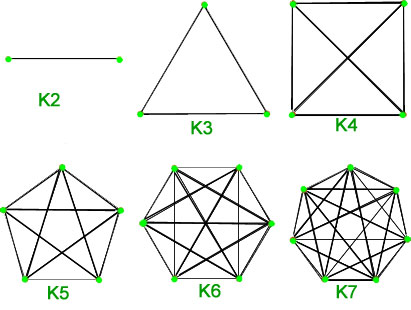
1. Úplné grafy – Jednoduchý graf 
vrcholů, který má mezi každou dvojicí vrcholů přesně jednu hranu, se nazývá úplný graf. Úplný graf o vrcholech se označuje 
. Celkový počet hran je n*(n-1)/2 s n vrcholy úplného grafu.
2. Cykly – Cykly jsou jednoduché grafy s vrcholy 
a hranami 
. Cyklus s vrcholy se označuje jako 
. Celkový počet hran je n s n vrcholy v grafu cyklu.
3. Kola – Kolo je stejně jako cyklus s jedním vrcholem navíc, který je spojen s každým dalším vrcholem. Kola o vrcholech s 1 přídavným vrcholem se označují 
. Celkový počet hran je 2*(n-1) s n vrcholy v grafu kola.
4. Hyperkostka – Hyperkostka neboli n-úhelník je graf s 
vrcholy, z nichž každý je reprezentován n-bitovým řetězcem. Vrcholy, které se liší nejvýše o 1 bit, jsou spojeny hranami. Hyperkostka o vrcholech se označuje 
. Celkový počet hran je n*
s vrcholy v krychlovém grafu.
5. Bipartitní grafy – O jednoduchém grafu se říká, že je bipartitní, jestliže jeho množinu vrcholů lze rozdělit na dvě nesouvislé množiny tak, že každá hrana v má počáteční vrchol v první množině a koncový vrchol v druhé množině. Celkový počet hran je (n*m) s (n+m) vrcholy v bipartitním grafu.
Věta – Jednoduchý graf je bipartitní tehdy a jen tehdy, jestliže je možné každému vrcholu grafu přiřadit jednu ze dvou
různých barev tak, že žádným dvěma sousedním není přiřazena
stejná barva.
O bipartitním grafu s 
a vrcholy v jeho dvou nesouvislých podmnožinách se říká, že je úplný, jestliže existuje hrana z každého vrcholu první množiny do každého vrcholu druhé množiny, celkem tedy 
hran. Úplný bipartitní graf s vrcholy v první množině a vrcholy ve druhé množině se označuje jako 
.
GATE CS Corner Questions
Procvičení následujících otázek vám pomůže ověřit si své znalosti. Všechny otázky byly položeny v předchozích letech v rámci GATE nebo ve zkušebních testech GATE. Důrazně doporučujeme, abyste si je procvičili.
1. GATE CS 2013, otázka č. 25
2. GATE CS 2014 Set-1, otázka č. 61
3. GATE CS 2006, otázka č. 71
4. GATE CS 2002, otázka č. 25
5. GATE CS 2014 Set-1, otázka č. 61
6. GATE CS 2006, otázka č. 71
737. GATE CS 2004, Question 37
6. GATE CS 2014 Set-2, Question 13
References-
Graphs – Wikipedia
Discrete Mathematics and its Applications, by Kenneth H Rosen
Tento článek napsal Chirag Manwani. Pokud se vám GeeksforGeeks líbí a chtěli byste přispět, můžete také napsat článek pomocí stránky contribute.geeksforgeeks.org nebo poslat svůj článek na adresu [email protected]. Uvidíte, jak se váš článek objeví na hlavní stránce GeeksforGeeks, a pomůžete tak ostatním geekům.