Kvadraturní signály, nazývané také IQ signály, IQ data nebo IQ vzorky, se často používají v RF aplikacích. Tvoří základ komplexní modulace a demodulace VF signálů, a to jak v hardwaru, tak v softwaru, a také při analýze komplexních signálů. Tento příspěvek se zabývá pojmem IQ signály a jejich použitím.
O dvojici periodických signálů se říká, že jsou v „kvadratuře“, pokud se jejich fáze liší o 90 stupňů. „Fázový“ nebo referenční signál se označuje jako „I“ a signál, který je posunutý o 90 stupňů (signál v kvadratuře), se nazývá „Q“. Co to znamená a proč nás to zajímá? Rozebereme si to tak, že začneme od základů.
Základy VF modulace
Začneme přehledem jednoduché VF modulace. Nemodulovaná RF nosná je jednoduše sinusovka, jak je znázorněno níže.
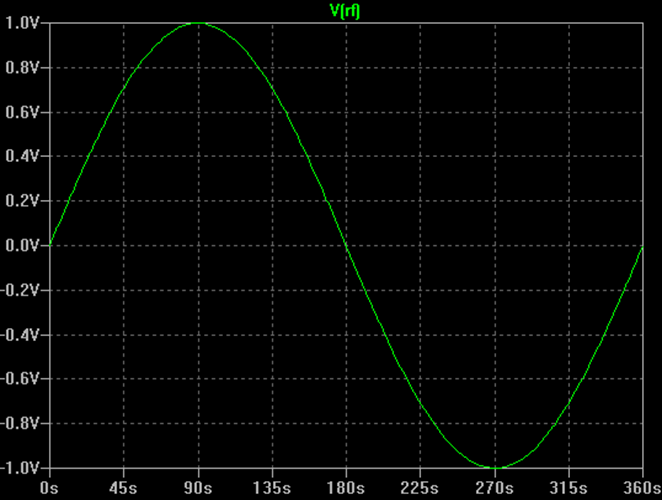
Signál lze popsat jako funkci času následující rovnicí:
V(t) = A * sin (2 * π * f * t + Ф)
kde:
A: je špičková amplituda
f: je frekvence
t: je čas
Ф: je fázový posun
Informace je „přenášena“ RF nosnou procesem modulace. Informační signál (hlas, data atd.) se používá ke změně vlastností VF signálu. Jednoduchým příkladem je amplitudová modulace neboli AM.
Při AM se informační signál používá ke změně nebo modulaci amplitudy nosné. Matematicky ji lze znázornit změnou konstanty „A“ v předchozí rovnici na nějaký časově proměnný signál (informační signál):
V(t) = A(t) * sin (2 * π * f * t + Ф)
Informační signál, známý také jako signál základního pásma, se s časem mění mnohem pomaleji než VF signál. Proto, abyste viděli vliv modulace, musíte pozorovat obálku VF signálu v delším časovém měřítku, jak je uvedeno níže.
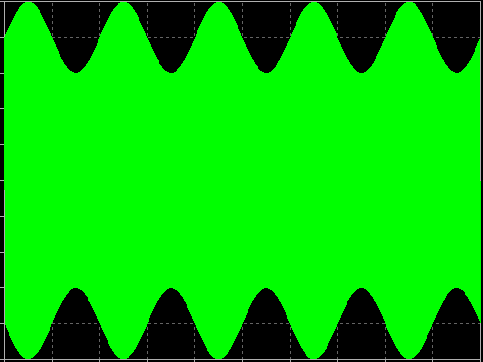
V tomto případě je signál A(t) sinusoidou. Obrázek ukazuje, jak amplituda VF signálu sleduje sinusový signál základního pásma A(t).
To můžete rozšířit tím, že si uvědomíte, že další vlastnosti VF nosné mohou být změněny nebo modulovány signálem základního pásma v závislosti na čase. Pokud je frekvence modulována základním pásmovým signálem, máme frekvenční modulaci (FM). Podobně, pokud je modulována fáze, máme fázovou modulaci (PM). Tedy:
- A(t) je, když se mění amplituda v závislosti na čase
- f(t) je, když se mění frekvence v závislosti na čase
- Ф(t) je, když se mění fáze v závislosti na čase.
Zapomeňte na základní pojem modulace, když navazujeme na pojem kvadraturních signálů…
Pojmy kvadraturních signálů
Je-li rozdíl fází Ф mezi dvěma sinusoidami 90 stupňů (nebo π /2 radiánů), pak se o těchto dvou signálech říká, že jsou v kvadratuře. Příkladem je sinusovka a kosinusovka.
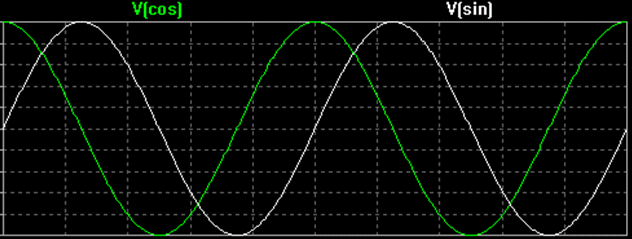
Podle konvence je kosinusovka fázovou složkou a sinusovka kvadraturní složkou. Velké písmeno I představuje amplitudu in-fázového signálu a velké písmeno Q představuje amplitudu kvadraturního signálu.
Použití kvadraturních signálů k modulaci
Zajímavé věci se stanou, když se podíváte na sčítání kvadraturních signálů dohromady.
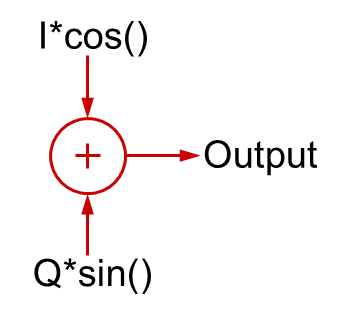
Pokud by I=1 a Q=0, pak byste měli jednoduše kosinusovou vlnu (fáze rovna 0). Podobně pokud by I=0 a Q=1, měli byste sinusovku, což je signál posunutý o 90 stupňů.
Pokud by I i Q byly rovny 1, pak součtem vznikne nový signál, který je graficky znázorněn níže.
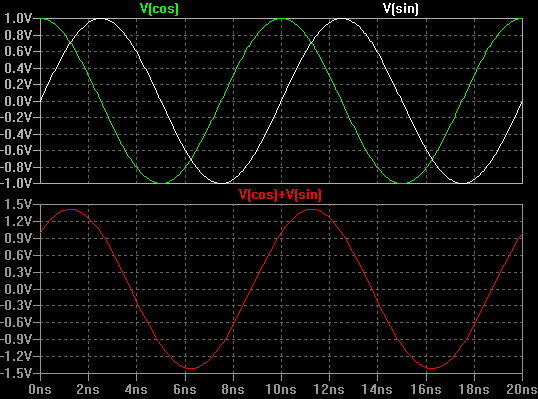
Všimněte si, že součtem těchto dvou kvadraturních signálů o stejné amplitudě vznikne nová sinusovka, která je fázově posunuta o 45 stupňů.
Teď už vidíte, že amplituda a fáze součtu kvadraturních signálů je funkcí hodnot I a Q. Proto můžete vytvářet modulované VF signály změnou hodnot I a Q v závislosti na čase. Podívejme se na několik příkladů.
Příklady digitální RF modulace
Pokud je Q=0 a I se v čase mění mezi +1 a -1, vytvoříte RF signál s binárním fázovým posunem (BPSK):
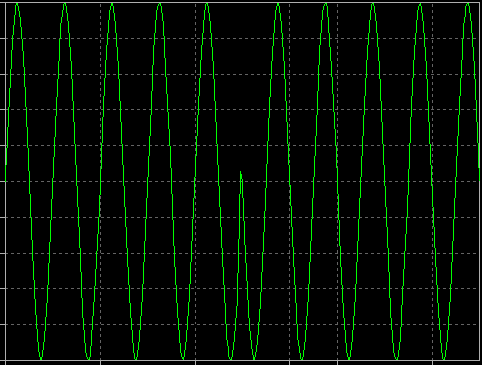
Signál I(t) může být jednoduchý digitální proud bitů. Pokud tímto signálem necháte řídit zesílení VF sinusoidy mezi +1 a -1, vytvořili jste signál BPSK.
Pokračujeme-li o krok dále… Pokud pomocí dvou digitálních bitů řídíte hodnoty I a Q mezi +1 a -1 v čase, pak výsledný součet kvadraturních signálů může mít jednu ze čtyř různých fází:
- I=+1 & Q=+1 vede k fázi 45 stupňů
- I=-1 & Q=+1 vede k fázi 135 stupňů
- I=-1 & Q=-1 vede k fázi 225 stupňů
- I=+1 & Q=-1 vede k fázi 315 stupňů
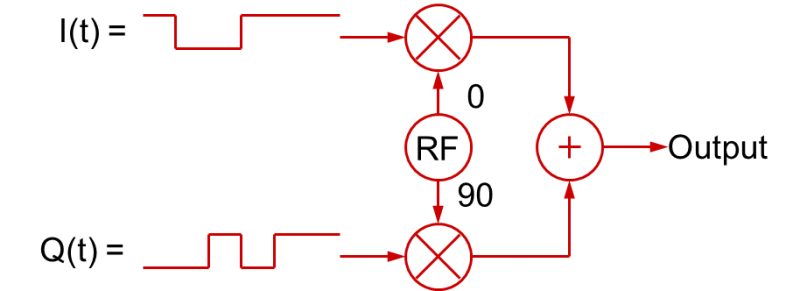
Tato modulace se nazývá kvadraturní modulace s fázovým posunem (QPSK). Toto jsou dva příklady kvadraturní amplitudové modulace (QAM). Různé modulační stavy pro QAM se často zobrazují na konstelačním diagramu. Konstelační diagram je jednoduše fázorový diagram, který zobrazuje amplitudu a fázi signálu jako polární graf.
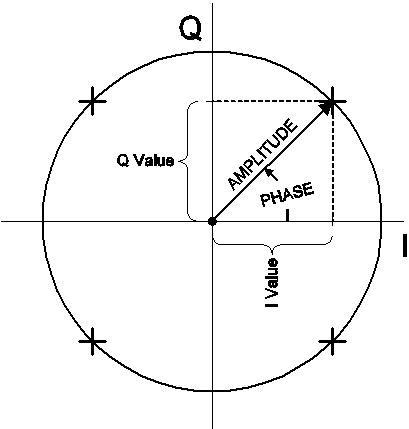
Délka vektoru od počátku představuje velikost signálu a úhel, který vektor svírá s vodorovnou osou, představuje fázi. Čtyři „stavy“ pro výše popsaný signál QPSK jsou v diagramu znázorněny jako čtyři symboly „+“. Všimněte si také, že vodorovná osa je označena „I“ a svislá osa je označena „Q“ – protože představují hodnoty složek I a Q spojené se signálem.
Složitější modulace QAM, například 16QAM, mají jednoduše více stavů. U 16QAM může každá z hodnot I a Q nabývat jedné ze čtyř diskrétních hodnot, což dává 16 možných kombinací. Výsledkem je 16 kombinací amplitudy a fáze VF signálu.
Kvadraturní signály všude
Používání I a Q signálů, které se mění v čase, k vytváření modulovaných VF signálů není omezeno na digitální signály základního pásma. Signály základního pásma I(t) a Q(t) mohou být také analogové signály základního pásma. ve skutečnosti jsou ve většině „digitálně“ modulovaných RF aplikací, jako je QPSK nebo nQAM, signály základního pásma filtrovány, aby se zpomalily přechody. To se provádí proto, aby se omezila výsledná šířka pásma modulovaného RF signálu (rychlé digitální doby náběhu a pádu zabírají velkou šířku pásma!). Tyto filtrované digitální signály jsou ve skutečnosti analogové signály! V obecnějším smyslu lze tedy proces kvadraturní modulace znázornit podle tohoto obrázku:
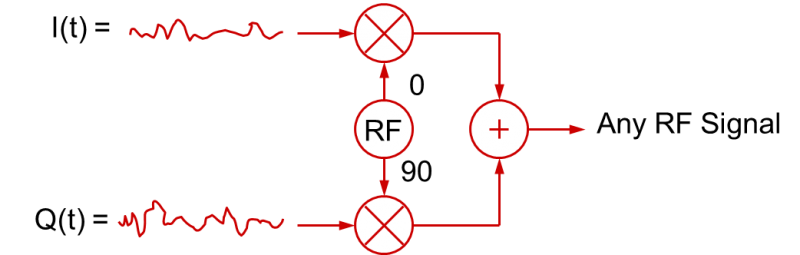
Obecný závěr, který z toho můžete vyvodit, je, že VF signál s libovolným typem modulace lze vytvořit pomocí vhodných signálů základního pásma I(t) a Q(t) (které zase mění amplitudy kosinových a sinusových vln, které se sčítají dohromady).
Stejný proces samozřejmě funguje i obráceně při demodulaci VF signálu. Smícháním VF signálu se signály LO (lokálního oscilátoru) v kvadratuře lze vytvořit signály základního pásma I(t) a Q(t).
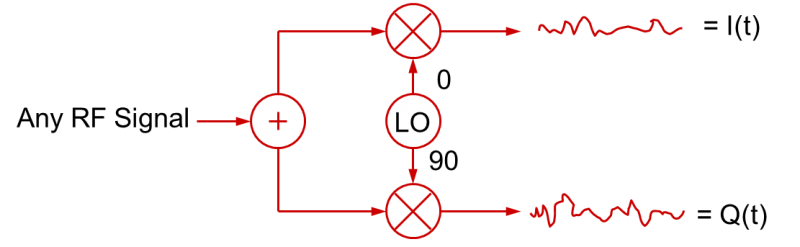
To je základní základ pro většinu moderních generací a modulací VF signálů, stejně jako pro demodulaci a vektorovou analýzu signálů.
Systémy softwarově definovaného rádia (SDR) tyto koncepty hojně využívají, protože signály základního pásma I &Q jsou často reprezentovány jako diskrétní časově vzorkovaná data. Proto lze digitální zpracování signálu (DSP) použít k doslovnému definování vlastností vysílače a přijímače včetně filtrace, modulace a demodulace, AGC atd. Přijímače SDR mají často šířku základního pásma několik set kHz nebo více, což jim dává možnost provádět širokou škálu funkcí, včetně funkcí „širokého“ pásma a spektrogramu, a také možnost současně sledovat a demodulovat několik signálů různých typů najednou.
Generátory vektorových signálů mají kvadraturní modulátor, který přijímá signály I(t) a Q(t), které pak používá k amplitudové modulaci dvojice kvadraturních sinusoid, které se pak sčítají a vytvářejí modulovaný VF výstup. Mnoho generátorů vektorových signálů obvykle obsahuje panelové konektory, kam lze připojit vlastní signály IQ. Mnohé z nich obsahují interní generátor libovolného tvaru vlny (AWG) pro vytvoření signálů IQ v základním pásmu.
Moderní vektorové analyzátory signálů mají obvykle šířku pásma 25, 40, 110 MHz nebo více. Převádějí příchozí VF signály na jejich I a Q složky. Veškerá analýza (spektrální analýza v závislosti na čase, demodulace, impulsní analýza atd.) je jednoduše různé matematické zpracování stejných dat IQ. Analyzátory signálů v reálném čase, jako je řada Tektronix RSA5000 a RSA6000, mají navíc schopnost přijímat „živé“ datové toky IQ a provádět zpracování dat v reálném čase. To přidává možnost provádět takové činnosti, jako je vizualizace živého spektra VF signálu, a také možnost spouštět přechodné události, které mohou být viditelné pouze ve frekvenční oblasti.
Podívejte se na nejnovější nabídku spektrálních analyzátorů Tektronix.
.