Rentgenová difrakce je běžná technika charakterizace materiálů, která umožňuje identifikovat krystalové orientace a meziatomové vzdálenosti. Rentgenové záření se k tomuto účelu používá proto, že jeho vlnová délka je na stejné délkové škále jako hodnoty meziatomových vzdáleností a mřížkových parametrů.
Co se děje?
Rentgenové záření se generuje ve vakuové trubici zahřátím wolframového vlákna za hranici jeho pracovní funkce, aby došlo k vyražení elektronů. Podmínky vakua jsou nezbytné pro zvýšení střední volné dráhy elektronů. Elektrony jsou urychlovány do měděné katody s energií řádově 25 keV. Srážky elektronů s měděnou katodou vedou k ionizaci vnitřního obalu a vzniku rentgenového záření, protože elektrony s vyšší energií klesají, aby zaplnily volné místo s nižší energií. Elektrony z různých vyšších energetických hladin klesají a vytvářejí elektromagnetické vlny s různou energií. Vzniká tak rentgenové záření několika vlnových délek (typu K-beta a K-alfa). Pro rentgenovou difrakci je ideální, aby se vzorkem interagovalo monochromatické světlo, proto se rentgenové záření K-beta filtruje pomocí niklové destičky. Přestože skutečně existují dvě přidružené energie K-alfa, jsou si energie natolik podobné, že to nemá významný vliv na celkový profil píku. Rentgenové záření prochází kolimátorem, který upravuje šířku svazku.
Malé pozadí s Braggovým zákonem
Braggův zákon popisuje vztah pro konstruktivní interferenci, kdy rentgenové záření o vlnové délce λ dopadající na materiál pod úhlem θ je difraktováno krystalovými rovinami oddělenými vzdáleností d a n představuje celé číslo.
Jak je uvedeno níže, fázový posun vlny způsobuje buď konstruktivní interferenci, jak je znázorněno vlevo, nebo destruktivní interferenci, znázorněnou vpravo, v závislosti na úhlu 2θ.
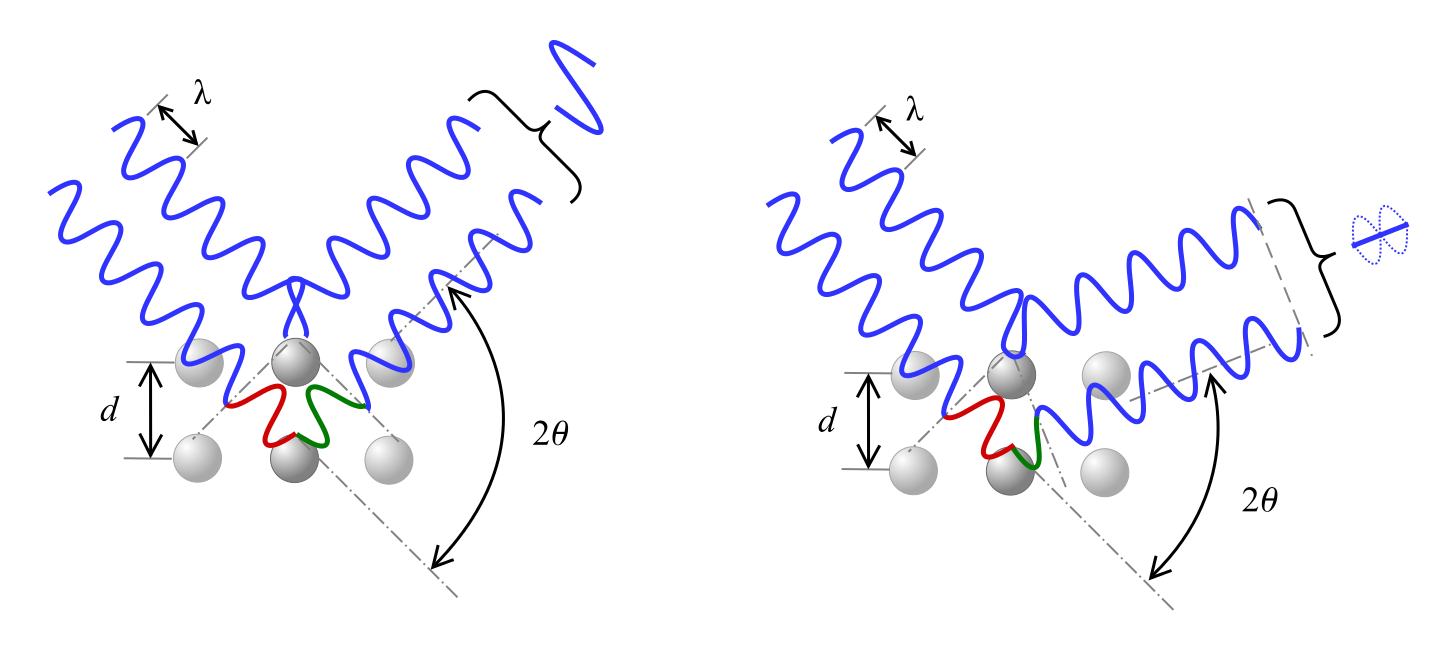
Rovnice pro interpretaci výsledků XRD
Čítač, který je vidět níže na schématu rentgenového difraktometru, se otáčí v rozsahu hodnot 2θ a zaznamenává intenzitu rentgenového signálu odraženého od krystalu v každé poloze. Tato intenzita měřená jako funkce 2θ se používá k vytvoření profilu píku.
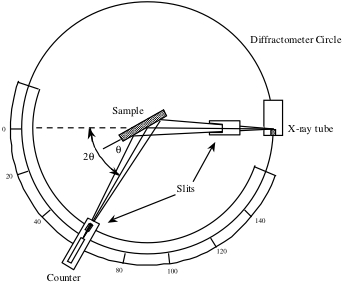
Při úhlech, které splňují Braggovu podmínku, bude pozorován pík rentgenového signálu v důsledku konstruktivní interference. Tyto píky se pak používají k identifikaci krystalových směrů a k výpočtu mřížkových parametrů. Pro kubické systémy lze meziplanární vzdálenost d vypočítat podle následující rovnice odvozené z geometrie krystalu, kde a je mřížkový parametr a h, k a l jsou Millerovy indexy.
Kombinace Braggova zákona a meziplanární vzdálenosti dává následující rovnici.
V tomto případě jsme všechny konstanty přesunuli na levou stranu rovnice, což nám umožňuje porovnávat poměry hodnot sin2(θ) a Millerových indexů mezi různými vrcholy.
Při dopadu dopadající elektromagnetické vlny na materiál vzorku jsou elektrony sídlící s materiálem rozrušeny do oscilačního vzoru, který generuje nové rentgenové záření a účinně rozptyluje dopadající světelné vlny. Dochází ke dvěma typům rozptylu: koherentní neboli pružný rozptyl zahrnuje pevně vázané oscilující elektrony, které rozptylují rentgenové záření stejné vlnové délky, a nekoherentní rozptyl, k němuž dochází, když jsou volně vázané elektrony uvedeny do oscilačního pohybu a generují rentgenové záření s různou energií. Difrakce rentgenového záření měří intenzitu koherentně rozptýleného rentgenového záření, které dosahuje vrcholu v místech, kde vlny konstruktivně interferují. Faktor atomového rozptylu lze definovat jako poměr amplitudy vlny rozptýlené atomem a amplitudy vlny rozptýlené jedním elektronem. Tento poměr v podstatě popisuje účinnost rozptylu atomu pro daný směr.
Příklad dat XRD
Tady jsou data získaná z experimentu, který jsem provedl během svého bakalářského laboratorního kurzu a snažil se identifikovat neznámý kov na základě jeho krystalové struktury.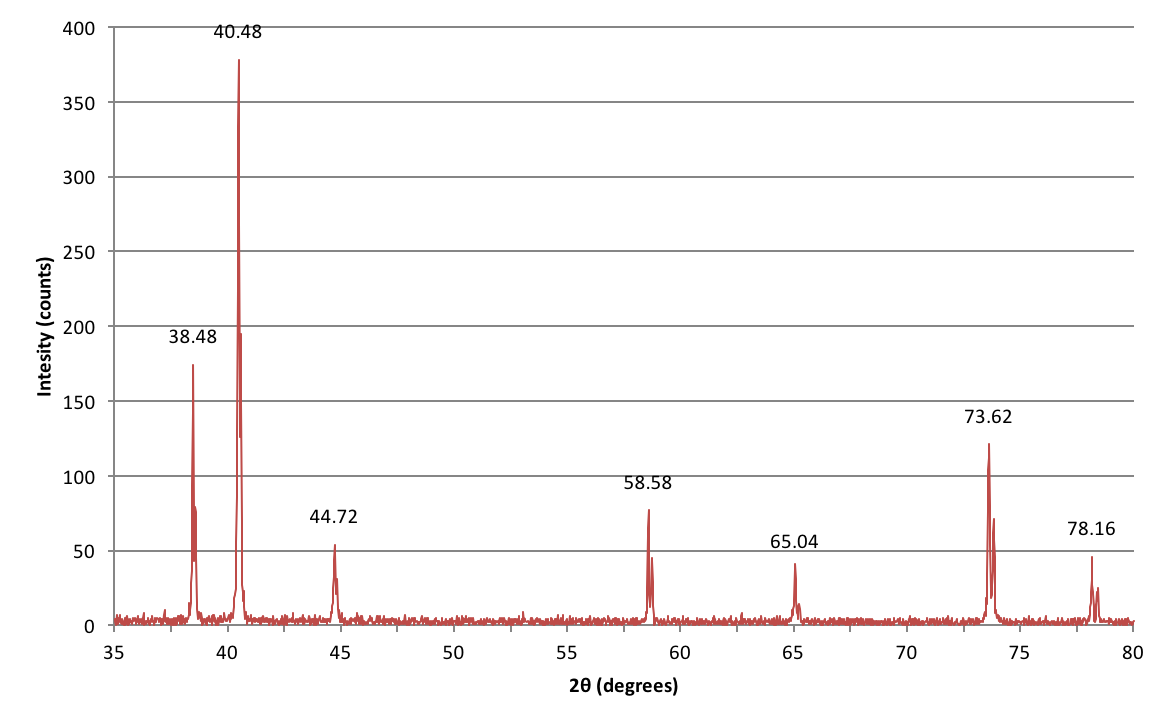
Jak mám tyto píky interpretovat?
| Krystalová struktura | Podmínky |
|---|---|
| Prostá krychle | vše h, k, l |
| Kubické těleso se středem | h+k+l musí být sudé |
| Kubické těleso se středem | h, k a l musí být všechny liché nebo všechny sudé |
Strukturní faktory zohledňují případy, kdy rovina může existovat na půli cesty mezi dvěma sousedními rovinami a způsobuje destruktivní interferenci. Výsledkem těchto faktorů je soubor pravidel pro různé geometrie krystalové struktury, která určují, kdy může dojít ke konstruktivní interferenci. Výše uvedená tabulka uvádí parametry Millerova indexu, při kterých dojde ke konstruktivní interferenci. Rozsáhlejší tabulka je uvedena níže. Porovnáním poměrů sin2θ (v druhé tabulce označených jako $Q^2$) pro různé difrakční píky lze určit krystalovou strukturu a Millerovy indexy.
| Krystalová rovina (hkl) | $Q^2$ | Prostor mřížek, od kterých jsou možné odrazy | ||||
|---|---|---|---|---|---|---|
| 100 | 1 | SC | ||||
| 110 | 2 | SC | BCC | |||
| 111 | 3 | SC | FCC | DC | ||
| 200 | 4 | SC | BCC | FCC | ||
| 210 | 5 | SC | ||||
| 211 | 6 | SC | BCC | |||
| – | 7 | |||||
| 220 | 8 | SC | BCC | FCC | DC | |
| 300, 221 | 9 | SC | ||||
| 310 | 10 | SC | BCC | |||
| 311 | 11 | SC | FCC | DC | ||
| 222 | 12 | SC | BCC | FCC | ||
| 320 | 13 | SC | ||||
| 321 | 14 | SC | BCC | |||
| – | 15 | |||||
| 400 | 16 | SC | BCC | FCC | DC | |
X-Difrakce paprsků má širokou škálu aplikací pro charakterizaci materiálů. Lze ji použít jako experimentální metodu k experimentálnímu určení objemu jednotkové buňky pro teoretické výpočty hustoty. Navíc, pokud je materiál pod zbytkovým napětím, bude deformovaná mřížka vykazovat řadu d-roztečí, které splňují Braggův zákon, což vede k mnohem širším difrakčním píkům. Šířku difrakčního píku lze také použít při určování velikosti částic
.