Introduction
In computer science, a directed acyclic graph (DAG) é um gráfico dirigido sem ciclos. Neste tutorial, vamos mostrar como fazer uma ordenação topológica em um DAG em tempo linear.
Topological Sort
Em muitas aplicações, usamos gráficos acíclicos dirigidos para indicar precedências entre os eventos. Por exemplo, em um problema de agendamento, há um conjunto de tarefas e um conjunto de restrições especificando a ordem dessas tarefas. Nós podemos construir um DAG para representar as tarefas. As bordas direcionadas do DAG representam a ordem das tarefas.
Vamos considerar um problema de como uma pessoa pode se vestir para uma ocasião formal. Precisamos de vestir várias peças de vestuário, tais como meias, calças, sapatos, etc. Algumas peças de vestuário devem ser vestidas antes das outras. Por exemplo, precisamos de usar meias antes dos sapatos. Algumas peças de vestuário podem ser colocadas em qualquer ordem, por exemplo, meias e calças. Podemos usar um DAG para ilustrar este problema:
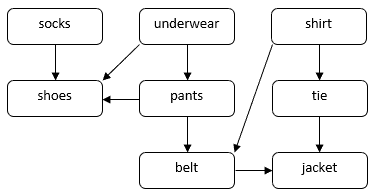
Neste DAG, os vértices correspondem às peças de vestuário. Uma borda direta 
no DAG indica que precisamos vestir a roupa 
antes da roupa 
. A nossa tarefa é encontrar uma ordem para vestir todas as peças de vestuário, respeitando as restrições de dependência. Por exemplo, podemos colocar as peças de vestuário na seguinte ordem:
Um tipo topológico de um DAG 
é uma ordenação linear de todos os seus vértices de tal forma que se contém uma borda , então aparece antes de na ordenação. Para um DAG, podemos construir uma ordenação topológica com tempo de execução linear ao número de vértices mais o número de arestas, que é 
.
Algoritmo do Kahn
Num DAG, qualquer caminho entre dois vértices tem um comprimento finito uma vez que o gráfico não contém um ciclo. Seja 
o caminho mais longo de (vértice fonte) a (vértice destino). Como é o caminho mais longo, não pode haver nenhuma borda de entrada para . Portanto, um DAG contém pelo menos um vértice que não tem borda de entrada.
3.1. Algoritmo de Kahn
No algoritmo de Kahn, construímos uma ordenação topológica num DAG encontrando vértices que não têm aresta de entrada:
Neste algoritmo, primeiro calculamos os valores em grau para todos os vértices.
Então, começamos com um vértice cujo grau de entrada é 0 e colocamo-lo no fim da lista de saída. Uma vez que escolhemos um vértice, atualizamos os valores em grau de seus vértices adjacentes porque o vértice e suas bordas de fora são removidos do gráfico.
Podemos repetir o processo acima até escolhermos todos os vértices. A lista de saída é então uma espécie topológica do gráfico.
3.2. Complexidade temporal
Para calcular os graus internos de todos os vértices, precisamos visitar todos os vértices e bordas de . Portanto, o tempo de execução é de para cálculos em graus. Para evitar o cálculo desses valores novamente, podemos usar um array para manter o controle dos valores em graus desses vértices. Dentro do loop while, nós também precisamos visitar todos os vértices e bordas. Portanto, o tempo total de execução é .
Depth First Search
Tambem podemos usar um algoritmo DFS (Depth First Search) para construir a ordenação topológica.
4.1. Gráfico DFS com Recursion
Antes de abordarmos o aspecto de ordenação topológica com DFS, comecemos por rever um algoritmo de traversal DFS padrão e recursivo:
No algoritmo DFS padrão, começamos com um vértice aleatório em e marcamos este vértice como visitado. Então, chamamos recursivamente a função dfsRecursive para visitar todos os seus vértices adjacentes não visitados. Desta forma, podemos visitar todos os vértices de em tempo.
No entanto, como estamos colocando cada vértice na lista imediatamente quando o visitamos, e como podemos começar em qualquer vértice, o algoritmo DFS padrão não pode garantir a geração de uma lista ordenada topologicamente.
Vejamos o que precisamos fazer para resolver esta falha.
4.2. Algoritmo de ordenação topológica baseado na DFS
Podemos modificar o algoritmo DFS para gerar uma ordenação topológica de um DAG. Durante a travessia DFS, depois que todos os vizinhos de um vértice são visitados, nós então o colocamos para a frente da lista de resultados 
. Desta forma, podemos garantir que aparece antes de todos os seus vizinhos na lista ordenada:
Este algoritmo é semelhante ao algoritmo padrão da DFS. Apesar de ainda começarmos com um vértice aleatório, não colocamos o vértice na lista imediatamente depois de o visitarmos. Em vez disso, primeiro visitamos todos os seus vizinhos recursivamente e depois colocamos o vértice na frente da lista. Portanto, se contém uma borda , então aparece antes de na lista.
O tempo total de execução também é , pois tem a mesma complexidade de tempo do algoritmo DFS.
Conclusão
Neste artigo, mostramos um exemplo de ordenação topológica em um DAG. Também, discutimos dois algoritmos que podem fazer uma ordenação topológica em time.
A implementação Java do algoritmo de ordenação topológica baseado na DFS está disponível em nosso artigo em Depth First Search in Java.