Quantos lados tem um círculo?

É uma questão de lição de casa da escola primária que causa discordância entre matemáticos experientes. A fim de encontrar a resposta correta, eu chamei a mais rigorosa dos instrumentos científicos, a pesquisa do Twitter:

Em retrospectiva eu lamento não incluir uma opção “nenhuma das acima”, mas mais sobre isso mais tarde. Neste post vou analisar essas três respostas (e “nenhuma das acima”), e discutir seus prós e contras como os vejo, antes de revelar dramaticamente a resposta correta.

Mas primeiro: por que não podemos dar a resposta correta? As palavras na pergunta não são misteriosas. Todos sabemos o que é um “círculo”, o que significa contar “quantos” de algo, e o que é um “lado”… ou não sabemos? Aqui estão as definições (rudes) que eu destilei das discussões com dois alunos da escola primária que estavam no final receptor desta pergunta:

1. Uma linha que faz parte dos limites de uma forma de uma figura plana.

O propósito de dizer figura plana em vez de “forma” aqui é que queremos formas que vivem em 2 dimensões (por exemplo, quadrados ou círculos, mas não esferas ou cubos). A questão seguinte é o que é uma “linha” na definição 1. Aqui está uma variante que pinos para baixo:

2. uma linha reta formando parte do limite de uma figura plana.

Se você digitar “definir: lado” no Google, a definição mais relevante é:

Uma figura rectilínea é uma construída a partir de linhas rectas. Então esta definição é um refinamento da definição 2, e nos permite afirmar que um quadrado tem quatro lados, mas na face dele não tem nada a dizer sobre figuras não rectilíneas como círculos.

Infinitely Many Sides?

Eu acho que é uma aposta segura que os respondentes à minha pesquisa no Twitter têm um nível mais alto de educação matemática do que a média nacional. O fato de que eles estavam divididos nesta pergunta, e que uma pequena maioria selecionou uma resposta que está bem indisponível para o público habitual desta pergunta (alunos do ensino fundamental), certamente sugere algo errado em algum lugar.

Então, será que um círculo tem infinitos lados? É definitivamente útil considerar um círculo como o limite dos polígonos de n lados à medida que n fica maior e maior. Esta é exatamente a abordagem que Arquimedes, Liu Hui, e inúmeros outros têm usado ao longo dos séculos para estudar a geometria circular, inclusive chegando a aproximações para π.

Uma edição da dinastia Ming do século 16 do Jiuzhang suanshu (Nove Capítulos sobre a Arte Matemática), terceiro século EC.

Às vezes é absolutamente sensato, como uma conveniente estenografia, pensar num círculo como um polígono com infinitos lados.

Mas, como um pedante insuportável um matemático, eu gostaria de distinguir entre uma estenografia conveniente e a verdade literal. Se somos inflexíveis em afirmar que um círculo é realmente um polígono com infinitos lados, então a questão se apresenta: quais são os lados? E certamente a única resposta plausível é: os pontos individuais do círculo. Por quanto tempo são esses chamados lados? Zero centímetros. E esses lados estão separados por esquinas? Aparentemente não, ou não há cantos, ou cada ponto é tanto um lado como um canto.

Eu diria que lados de comprimento zero são… um conceito problemático. Como é que sabes se tens algum? Por exemplo, suponha que eu esteja estudando um sistema onde um quadrado surge como um limite de octógonos como este:

Nesta situação, poderia muito bem fazer sentido para mim pensar no meu quadrado como tendo oito lados, quatro dos quais têm comprimento zero. Mas se eu fosse insistir que meu quadrado (perfeitamente comum) realmente tem oito lados, você poderia levantar uma sobrancelha.

Então esta – a resposta vencedora na minha enquete – é a única que eu vou declarar como definitivamente errada, enquanto também é a única que oferece qualquer percepção geométrica. Um paradoxo? Nem por isso. Raciocinar por analogia é uma habilidade valiosa em matemática e na vida; ao mesmo tempo é importante agarrar-se à percepção de que é isso que estamos a fazer.

Para infinitos lados: iluminando geometricamente.
Against infinitamente muitos lados: quadrados de oito lados.

Off sobre uma tangente 1: apeirogons

Even se um círculo não é um, existem coisas como polígonos com infinitos lados? Bem, existe uma palavra para descrever tal coisa como um apeirogão. Um apeirogão regular teria então lados de comprimento igual (não-zero) com ângulos iguais entre eles. A única opção aqui é este objeto estupendamente instigante:

Se você se opuser a isto como sendo um “polígono” (seja por causa dos ângulos de 180° ou da cadeia de bordas que não se fecham em loop), que tal algo como isto: comece no fundo de um círculo, e em cada etapa mova-se cerca de metade do que resta do círculo, e substitua o arco que acabou de percorrer por uma aresta reta:

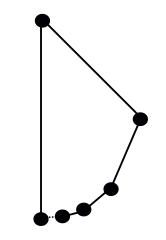
Este é um polígono genuíno? Mais uma vez, depende dos seus termos. De acordo com uma definição comum, a de uma “cadeia poligonal fechada”, esta não se qualifica uma vez que o canto inicial (inferior esquerdo) só se liga a uma aresta. Mas é uma falha muito próxima: esse ponto é o limite de uma sequência de arestas a partir da direita, fazendo desta forma uma “curva linear fechada não auto-intersectante”, outra definição de polígono que as pessoas usam.

Se sairmos do nosso mundo euclidiano habitual e entrarmos no espaço hiperbólico, então não há ambiguidade. Apeirogões (mesmo os apeirogões regulares) simplesmente existem:

Um mosaico do plano hiperbólico por apeirogões regulares. (Por Anton Sherwood – Trabalho próprio, Domínio Público, https://commons.wikimedia.org/w/index.php?curid=13260274 )

Off sobre uma tangente 2: pontos extremos

Pode ser mais defensável dizer que um círculo tem infinitos cantos do que infinitos lados (embora esta não seja uma pergunta que parece ser feita com muita frequência). Para começar, se um canto de um quadrado é um ponto em que sua linha limite não é reta, então cada ponto do círculo satisfaz isso. Mais sofisticadamente, há a noção de um ponto extremo de uma forma: esse é qualquer ponto através do qual se pode desenhar um segmento de linha reta que só toca a forma nesse ponto exato. Para um quadrado e muitas formas familiares, os pontos extremos coincidem exactamente com os cantos. Cada ponto no limite da circunferência é um ponto extremo, então é certamente verdade que uma circunferência tem infinitamente muitos.

Podemos nos preocupar que algumas formas como este chevron tenham cantos que não são pontos extremos:

Aqui o canto central inferior não é um ponto extremo (os outros três cantos são). O que está a correr mal é que esta forma não é convexa (mais ou menos, tem alguns bocados a sair demasiado para fora). Um círculo é convexo, então talvez não precisemos nos preocupar. Alternativamente, podemos remediar a situação definindo um “canto” para ser um ponto que é um ponto extremo tanto da forma em questão como do seu complemento, ou seja, todo o plano com a forma recortada dele. Essa abordagem detectaria os cantos de todos os polígonos, incluindo o chevron. Para curvas suaves, ela identificaria todos os pontos de contorno como “cantos”, exceto os pontos de inflexão (o que não é irracional, pois podemos argumentar que o limite é reto ali).

Um Lado?

Na escola primária, parece que “um” é a resposta que recebe o carrapato. E há uma justificação moderadamente decente. Lembre-se da definição 1 acima:

1. Uma linha que faz parte do limite de uma figura plana.

A questão imediata é o que conta como uma “linha”, especialmente se não estivermos insistindo em retidão. Se estivermos muito relaxados sobre isso, então qualquer figura plana poderia ser dita como tendo “um lado”, no mesmo sentido que tem um limite, perímetro ou circunferência. Mas isto tem que estar errado, já que nós certamente queremos um quadrado para ter quatro. Bem, um quadrado tem quatro pontos onde não é liso, com quatro secções lisas no meio. Talvez fossem mesmo as secções lisas que estávamos sempre a contar. Então implicitamente temos um novo refinamento da definição 1 (e também aproveitamos a oportunidade para abandonar o termo vago “figura”):

4. Cada secção lisa de uma curva fechada de uma peça lisa.

Uma “curva fechada” é aquela que se localiza para se encontrar a si própria de modo a não ter pontas livres. “Lisa” significa que ela é construída a partir de seções lisas, que se encontram em pontos não lisas isolados. É perfeitamente legítimo querer contar as seções lisas do limite de tal forma, e não é de forma alguma ultrajante usar a palavra “lado” ao fazer isso. Portanto, certamente não estou dizendo que esta é definitivamente a resposta errada.

A questão é se essa interpretação de “lado” não é meramente coerente, mas natural o suficiente para que possa ser simplesmente presumida sem ser declarada explicitamente (o que raramente ou nunca é). O que acontece quando a lisura e a retidão se acumulam de forma diferente? Considere esta forma de pedra tumular, criada pela substituição do topo de um quadrado por um semicírculo de igual diâmetro.

Esta tem duas secções lisas (a linha inferior e o resto), mas três arestas rectas (mais uma peça curva unindo suavemente duas delas). Quantos lados tem? Eu consultei meus amigos do Twitter novamente:

Desta vez eu deveria ter incluído “infinitamente muitos” como opção, embora isso possa ser absorvido em “Nenhum dos acima”. Quem votar que o círculo tem infinitamente muitos lados deve votar automaticamente “Nenhum dos acima” aqui, a menos que – uma importante advertência – a natureza desta forma indique ao leitor uma noção diferente de “lado”. O facto de as escolhas mais populares nestas duas sondagens serem incompatíveis sugere que este pode ser o caso (ou pelo menos reforça que as águas estão lamacentas).

Embora duas seja uma resposta perfeitamente respeitável, compatível com a definição 4 acima e com a unilateralidade de um círculo, não estou satisfeito que seja definitivamente a correcta, ou que três ou quatro estejam categoricamente errados. Depende do que você quer contar: seções lisas, bordas retas, ou bordas retas mais o que sobrar depois, qualquer uma das quais pode ser a resposta que você quer, dependendo do contexto (mais sobre isso abaixo). Relativamente, eu não tenho certeza se a contagem do número de seções lisas corresponde totalmente à minha intuição da palavra “lado”. Afinal, as duas secções verticais da lápide estão – penso que é justo dizer – “em lados opostos”. Estamos realmente satisfeitos que elas fazem simultaneamente parte do “mesmo lado”?

Você pode protestar que estou conflitando dois significados diferentes de “lado”, que a terminologia às vezes se choca, e nós só temos que viver com isso. Mas não tenho tanta certeza. O objectivo deste exercício é extrapolar a partir de uma situação (figuras rectilíneas) em que as duas noções se interligam bastante bem. Se houvesse uma nova ideia que captasse tudo o que gostávamos sobre o original, mas que também se aplicasse a uma categoria mais ampla de formas, então isso teria uma pretensão esmagadora de ser a resposta única e correcta. Mas se todas as nossas tentativas de generalização envolvem o sacrifício de aspectos desejáveis do original, então talvez não haja uma única generalização correta. Existem escolhas diferentes, com diferentes trade-offs, que podem ser adequadas em contextos diferentes (e se estivermos numa situação em que mais do que um está em jogo, então poderiam ajudar a dar nomes diferentes).

Há uma outra variação: uma lápide de Weierstrass criada pela substituição da borda superior de um quadrado por uma secção da função Weiestress, uma linha infinitamente periclitante que não é lisa em lado nenhum.

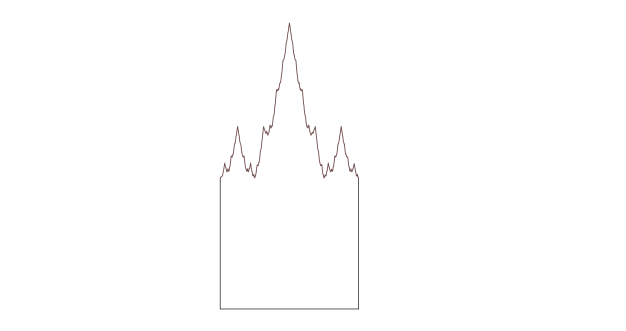
Aqui (e localizar a gralha) foi o que os meus amigos do Twitter fizeram disso – embora menos se aventurem a ter uma opinião:

Não obstante o ceticismo dos meus seguidores do Twitter, explicarei em um minuto porque não acho bobo ver isso como tendo quatro lados (um dos quais não é liso). Por outro lado, se você preferir seus lados lisos, então você novamente tem uma escolha entre ver que tem infinitamente muitos lados (três dos quais têm comprimento 1, e o resto tem comprimento 0), ou ter 3 lados mais um trecho de limite definitivamente não-lateral.

Para um lado: uma única curva lisa.
Against one side: o mesmo lado em lados opostos.

Off on a tangent 3: sides versus edges

Quantos lados tem um quadrado? Quatro. Quantas arestas tem? Quatro. Então, as bordas e os lados são a mesma coisa? Não necessariamente. Aqui estão duas configurações que são – pelo menos discutivelmente – cada quatro lados mas têm 5 e 3 arestas respectivamente:

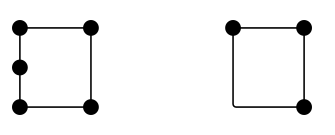
Usualmente, eu diria, uma “aresta” é um objeto topológico, na medida em que sua função, não sua forma, é o que importa. Pense no mapa do metro de Londres. Se você perguntar quantas bordas existem nessa rede, não há mérito em totalizar as seções retas ou lisas. São conexões entre estações (ou vértices) que contam.

Como já mencionado, é comum pensar num polígono como um tipo muito simples de rede chamada cadeia poligonal fechada: uma cadeia de vértices (neste caso os cantos do polígono), ligados com arestas, de tal forma que cada vértice fica exatamente em duas arestas, e a coisa toda forma um único laço. Nesta situação, as arestas e os lados coincidem, assim como os vértices e os cantos. Mas em geral você pode quebrar essa coincidência, como nas duas pequenas redes acima.

Se você quiser pensar em coisas de rede – teoricamente, mas os vértices não estão claramente marcados, então você tem que adivinhar onde eles estão. Com um polígono isto é fácil – os vértices estão nos cantos – e é por isso que alternar entre abordagens geométricas e topológicas vem de forma tão natural. Mas com outras formas, como qualquer uma das lápides acima, pode não ser tão óbvio. No entanto, em cada caso, se lhe dissessem que havia vértices em algum lugar, e lhe pedissem para localizá-los, acho que seria sensato adivinhar que existem quatro, a saber, os cantos do quadrado original, e que a borda superior foi representada, por alguma razão, como uma linha não-retaguarda. E se quisermos pensar assim, com cada uma das lápides a ter 4 arestas, então pode parecer perverso (embora logicamente coerente!) para insistir que eles têm algum outro número de lados (especialmente porque o lado superior está – apesar de sua própria geometria – claramente “de um lado” da figura). Na verdade, ao invés de adivinhar, um dos meus correspondentes do Twitter me perguntou “Os dois vértices superiores foram removidos?”, uma pergunta que só faz sentido de uma perspectiva teórica de rede.

Onde isso deixa o círculo? O problema é que nenhum ponto do círculo tem melhor pretensão de ser um vértice do que qualquer outro. Então embora seja tentador (e novamente coerente) ver um círculo como uma rede com uma borda, se vamos inserir vértices, não há nenhuma razão óbvia para preferir um a qualquer outro número.

Podemos vê-lo como uma rede sem vértices, uma espécie de linha de Tubo sem estações? A concepção matemática habitual de uma rede não permitiria isso, mas isso não nos deve dissuadir muito. Isto sugere uma abordagem puramente topológica. O problema é que desse ponto de vista, enquanto um círculo pode ser uma espécie de rede sem vértices e sem uma borda, também o é um quadrado (se é assim que a linha do Tubo é traçada). Em topologia, um quadrado é um círculo. (Isto não é um paradoxo, é simplesmente dizer que o limite é um único laço, cuja forma não importa). Assim, embora este tipo de rede tenha “uma borda”, obviamente um quadrado não tem “um lado”, então a relação entre os lados (geométricos) e as bordas (topológicos) foi novamente quebrada, tal como acontece nas duas pequenas redes retratadas acima. Portanto, esta aproximação não nos leva muito longe.

No Sides?

Pode parecer paradoxal argumentar que um círculo (ou qualquer forma) não tem “nenhum lado”. Mas o argumento para a defesa é simples. Voltamos à definição 2:

2. Uma linha reta que faz parte do limite de uma figura plana.

Esta é uma frase simples, facilmente compreensível, que captura perfeitamente os lados de um quadrado. Não conseguimos encontrar uma generalização satisfatória desta para figuras curvas, por isso o melhor a fazer é ficar com o original. E um círculo não tem nenhum.

Para nenhum lado: verdade, de acordo com uma noção sensata de “lado”.
Against no sides: soa como um koan Zen.

Nenhum dos Acima?

Recorde a definição fornecida pelo Google:

3. Cada uma das linhas que formam o limite de uma figura rectilínea plana.

Tentando aplicar isto a um círculo – uma figura não rectilínea – não produz nada. A questão é tão sem sentido como “Quantos lados tem a segunda-feira?”

Desde que a Definição 3 é a mais oficial (a única neste post não feita por mim ou pelos meus filhos), isso não faz de “Nenhum dos Acima” categoricamente a resposta certa? Talvez. Por outro lado: quando alguém nos faz uma pergunta, o princípio da caridade talvez exija que assumamos que ela é significativa, a menos que possamos estabelecer firmemente o contrário, e as definições 1, 2, 4 e outras variantes tornam isso possível. Além disso, a definição 3 é linguística em vez de formalmente matemática, e é portanto descritiva em vez de prescritiva, por isso não nos devemos esconder por ela.

Para nenhuma das anteriores: mau funcionamento semântico.
Against none of the above: dialogic charity.

The Right Answer

What prompted me to write this post? Como inúmeros alunos da escola primária, meus filhos gêmeos de cinco anos – os alunos da escola primária mencionados no início – foram recentemente questionados em seus deveres de casa. Um mergulhou para “1” e o outro “0”, e eu tentei captar e expandir o raciocínio deles acima. Eu acho que ambas as respostas são totalmente defensáveis – e nenhuma delas está definitivamente correta.

Então, o que você deve fazer se a pergunta lhe for feita? Quantos lados tem um círculo? Na minha opinião, a resposta ideal é abordar o matemático na sua vida para escrever um tratado de 3000 palavras sobre o tema, que você pode então imprimir e entregar triunfantemente ao seu infeliz professor. Mas se isso não acontecer, a melhor abordagem é seguir o exemplo de Sócrates e responder à pergunta com uma contra-question: O que você quer dizer com “lado”?

Quando tudo é dito e feito, contar até zero, ou para um, ou recusar-se a responder à pergunta, não nos diz praticamente nada sobre a geometria dos círculos. Mas há muito a ganhar se separarmos noções familiares, se deixarmos cair ou acrescentarmos condições extra, se desafiarmos a nossa intuição passando de um contexto para um ligeiramente diferente, e se tentarmos escrever precisamente o que queremos dizer com um determinado termo num determinado contexto. É disso que se trata a verdadeira matemática.

Footnotes

Você poderia fazer algo mais: por exemplo, escolher um ponto de partida P sobre o círculo, a partir do qual medir a distância ao redor da circunferência. Depois declare que os pontos a uma distância racional de P são cantos e o descanso são lados. Isto tem o efeito de produzir um número incontável e infinito de cantos e um número incontável de lados. Ou pode-se estipular o oposto. Isso pode ser um ajuste conveniente para a abordagem do limite poligonal dos círculos, mas eu teria dificuldade em concordar que é fácil ou óbvio o suficiente para ser considerado “a resposta certa”.

Um dos meus correspondentes do Twitter estava preocupado com o quão suave é a curva. Esta pedra tumular é continuamente diferenciável, mas não duas vezes. Seria certamente interessante se muitas pessoas pensassem que este era um assunto crítico, e isto provavelmente poderia ser testado com uma lápide infinitamente lisa construída a partir de algo assim, embora eu não tenha pensado nos detalhes.

Poderíamos tentar formalizar isto da seguinte forma: em um quadrado (ou qualquer polígono), um lado tem a propriedade de que a partir de qualquer posição no interior, você pode cortar a forma diretamente através do seu local, de modo que o seu lado escolhido esteja firmemente em um dos lados do corte. Isso não funciona para a pedra tumular de dois lados: qualquer corte cortará sempre o lado longo. Poderíamos enfraquecer isto dizendo que para contar como um lado, tem que haver pelo menos uma forma de cortar através da forma para que o lado esteja de um lado do corte. Isso nos permitiria dizer que a pedra tumular tem quatro lados (ainda que a seção curva não esteja em um lado dos pontos da região superior). Para o círculo, porém, o seu suposto lado nunca está de um lado (assim seria descartado), e apenas a seção reta de um semicírculo contaria como um lado.

Não é fácil chegar a uma justificação rigorosa que funcione para ambas as lápides, mas estou pensando mais informalmente em termos de Pontos de Esquemas: ou seja, locais que se destacam como especiais por razões que podem não ser fáceis de prever com antecedência.

Agradecimentos

Agradecimentos a todos que participaram ou retweetaram as minhas pesquisas, ou discutiram isso comigo no Twitter.