Probabilidade > Probabilidade Posterior & Distribuição Posterior
O que é a Probabilidade Posterior?
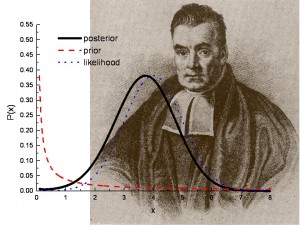
Probabilidades Posteriores são usadas em testes de hipóteses Bayesianas. Imagem: Los Alamos National Lab.
Probabilidade Posterior é a probabilidade de um evento acontecer depois de todas as evidências ou informações de base terem sido levadas em conta. Está intimamente relacionada à probabilidade anterior, que é a probabilidade de um evento acontecer antes de você levar em conta qualquer nova evidência. Você pode pensar na probabilidade posterior como um ajuste na probabilidade anterior:
Por exemplo, dados históricos sugerem que cerca de 60% dos alunos que iniciam a faculdade se formarão dentro de 6 anos. Esta é a probabilidade anterior. No entanto, você acha que esse número é na verdade muito mais baixo, por isso se proponha a coletar novos dados. As evidências que você coleta sugerem que o valor verdadeiro está mais próximo de 50%; Esta é a probabilidade posterior.
Origem dos Termos
As palavras posterior e anterior vêm do latim a priori. A definição de “a priori” é:
“…relacionado com o que pode ser conhecido através de uma compreensão de como certas coisas funcionam e não através da observação” ~ Miriam Webster.
O oposto de “a priori” é a posteriori, que é definido como:
“… relativo ao que pode ser conhecido através da observação e não através de uma compreensão de como certas coisas funcionam” ~ Miriam Webster.
O que é uma Distribuição Posterior?
A distribuição posterior é uma forma de resumir o que sabemos sobre quantidades incertas na análise Bayesiana. É uma combinação da distribuição anterior e da função de probabilidade, que lhe diz que informação está contida nos seus dados observados (a “nova evidência”). Em outras palavras, a distribuição posterior resume o que você sabe após os dados terem sido observados. O resumo da evidência das novas observações é a função de verossimilhança.
Distribuições posteriores são de importância vital na Análise Bayesiana. Elas são de muitas maneiras o objetivo da análise e podem lhe dar:
- Estimativas de intervalo para parâmetros,
- Estimativas de ponto para parâmetros,
- Previsão de inferência para dados futuros,
- Avaliações probabilísticas para suas hipóteses.
Stephanie Glen. “Probabilidade Posterior & a Distribuição Posterior” de StatisticsHowTo.com: Estatísticas Elementares para o resto de nós! https://www.statisticshowto.com/posterior-distribution-probability/>
——————————————————————————
Ajuda com um trabalho de casa ou pergunta de teste? Com o Chegg Study, você pode obter soluções passo-a-passo para suas perguntas de um especialista na área. Seus primeiros 30 minutos com um tutor do Chegg são grátis!