Difração de raios X é uma técnica comum de caracterização de materiais que permite a identificação de orientações de cristal e espaçamento interatómico. Os raios X são usados para isso porque o comprimento de onda está na mesma escala de comprimento que o espaçamento interatômico e os valores dos parâmetros da malha.
O que está acontecendo?
Um raio X é gerado em um tubo de vácuo através do aquecimento de um filamento de tungstênio além de sua função de trabalho para ejetar elétrons. As condições de vácuo são necessárias para aumentar o caminho livre da média dos elétrons. Os elétrons são acelerados em um cátodo de cobre com uma energia na ordem de 25 keV. As colisões dos elétrons com o cátodo de cobre resultam em ionizações internas do casco, produzindo raios X à medida que os elétrons de maior energia caem para preencher a vacância de menor energia. Os elétrons de vários níveis superiores de energia caem, produzindo ondas eletromagnéticas de energia variável. Assim, são gerados raios X de comprimentos de onda múltiplos (do tipo K-beta e K-alfa). Para difração de raios-x, é ideal ter luz monocromática interagindo com a amostra, assim os raios-x K-beta são filtrados com uma placa de níquel. Embora existam de facto duas energias K-alfa associadas, as energias são tão semelhantes que não afectam significativamente o perfil geral de pico. Os raios-x passam por um colimador para ajustar a largura do feixe.
Um pequeno fundo com a lei de Bragg
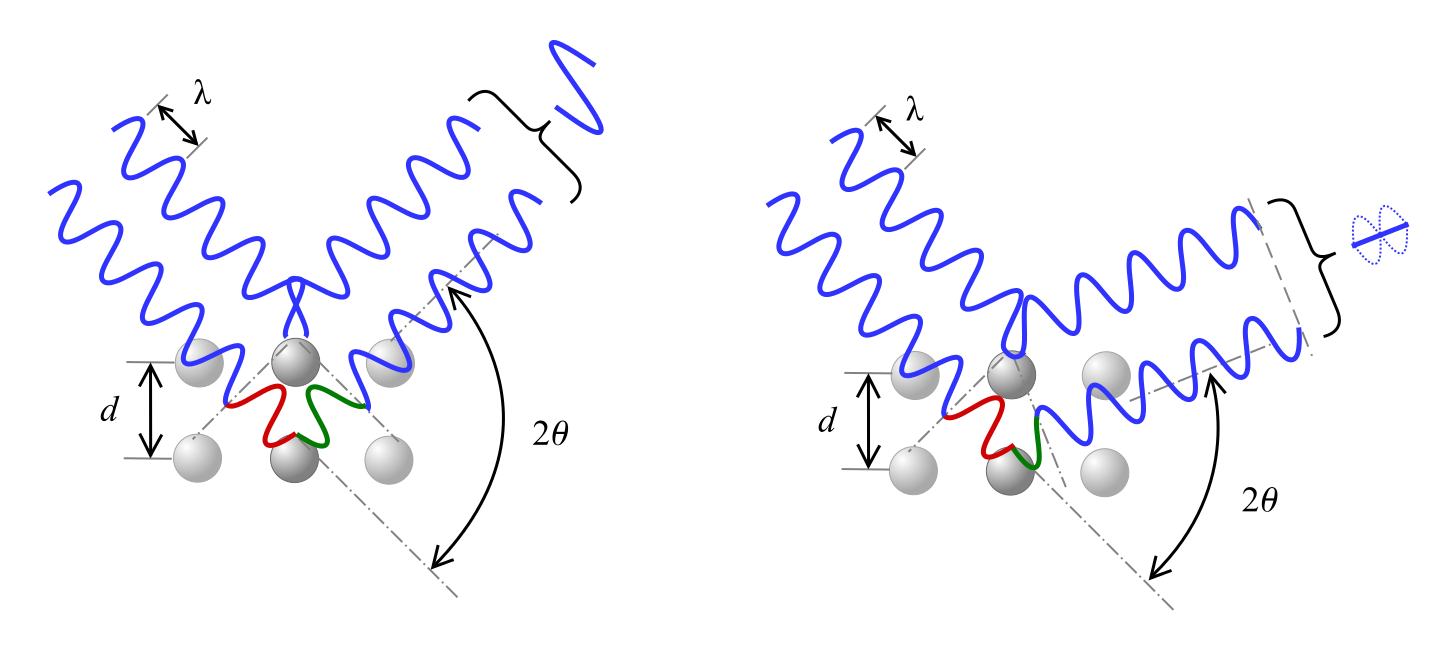
A lei de Bragg descreve a relação de interferência construtiva, onde os raios-x do comprimento de onda λ incidente no material no ângulo θ são difratados por planos de cristal separados pela distância d e n representa um inteiro.
Como mostrado abaixo, um deslocamento de fase na onda causa ou inferência construtiva, como mostrado à esquerda, ou interferência destrutiva, representada à direita, de acordo com o ângulo 2θ.
Equações para interpretação dos resultados do DRX
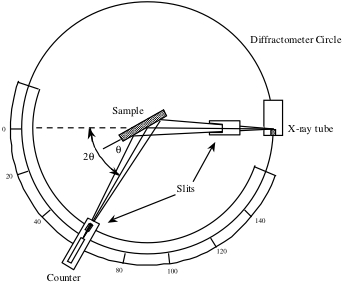
O contador, visto abaixo em um esquema de um difratômetro de raios-X, é girado em uma faixa de valores 2θ e registra a intensidade do sinal de raios-X refletido do cristal em cada posição. Esta intensidade medida em função do 2θ é usada para gerar um perfil de pico.
Para ângulos que satisfaçam a condição de Bragg, um pico no sinal de raio-x será observado devido à interferência construtiva. Estes picos são então usados para identificar as direções dos cristais e calcular os parâmetros da malha. Para sistemas cúbicos, o espaçamento interplanar, d, pode ser calculado pela seguinte equação derivada da geometria do cristal, onde a é o parâmetro da malha e h, k, e l são os índices Miller.
Combinando a lei de Bragg e o espaçamento interplanar produz a seguinte equação.
Aqui, movemos todas as constantes para o lado esquerdo da equação, permitindo-nos comparar proporções de valores de sin2(θ) e índices de Miller entre diferentes picos.
Quando a onda eletromagnética incidente colide com o material da amostra, os elétrons que residem com o material são perturbados em um padrão oscilante, o que gera novos raios X e efetivamente dispersa as ondas de luz incidentes. Dois tipos de dispersão ocorrem: a dispersão coerente ou elástica envolve elétrons oscilantes firmemente ligados que dispersam raios X do mesmo comprimento de onda, e a dispersão incoerente que ocorre quando elétrons frouxamente ligados são colocados em movimento oscilatório e geram raios X de energia diferente. A difração de raios-X mede a intensidade dos raios-X dispersos coerentemente, que atingem picos onde as ondas interferem de forma construtiva. O fator de dispersão atômica pode ser definido como uma razão entre a amplitude da onda dispersa por um átomo dividida pela amplitude da onda dispersa por um único elétron. Esta razão essencialmente descreve a eficiência de dispersão de um átomo para uma determinada direção.
Exemplo de dados do DRX
Aqui estão os dados coletados de uma experiência que fiz durante meu curso de graduação em laboratório tentando identificar um metal desconhecido baseado em sua estrutura cristalina.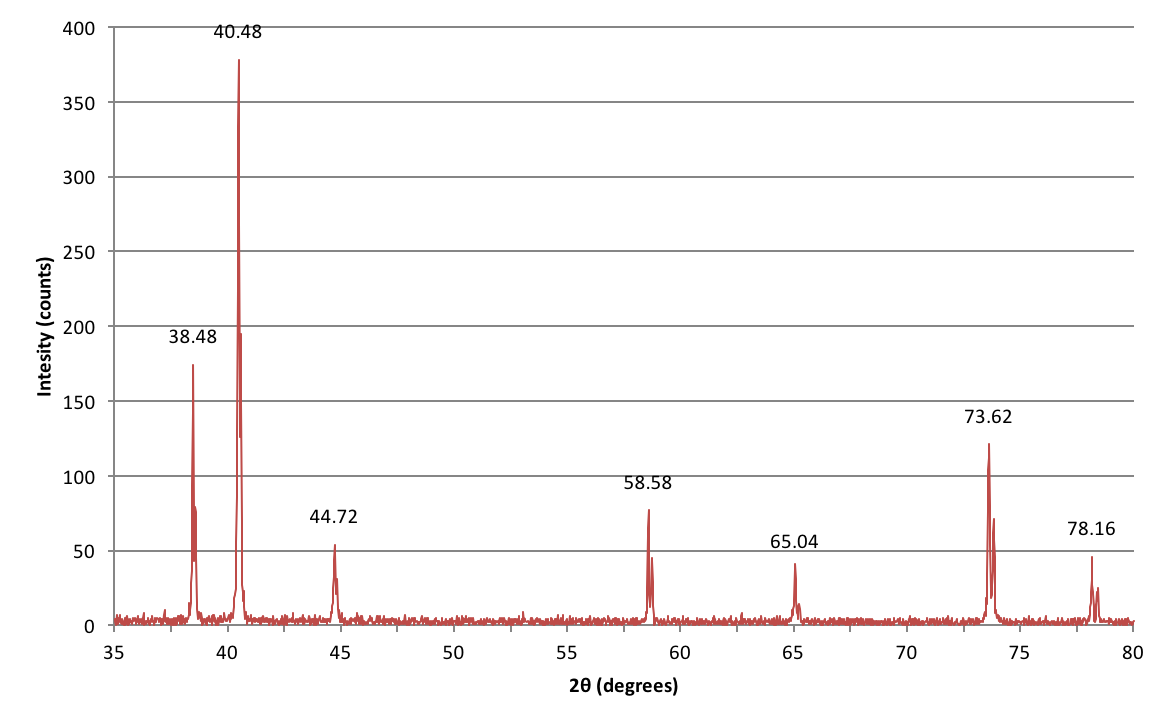
Como interpreto estes picos?
| Estrutura cristalina | Condições |
|---|---|
| Cúbico simples | todos os h, k, l valores |
| Cúbico Centrado no Corpo | h+k+l deve ser uniforme |
| Cúbico Centrado na Face | h, k, e l deve ser todo estranho ou todo par |
Os fatores de estrutura são responsáveis pelos casos em que um plano pode existir a meio caminho entre dois planos vizinhos e causar interferência destrutiva. Esses fatores resultam em um conjunto de regras para diferentes geometrias de estrutura de cristal que determinam quando a interferência construtiva pode ocorrer. A tabela acima lista os parâmetros do índice Miller nos quais a interferência construtiva irá ocorrer. Uma tabela mais extensa é mostrada abaixo. Comparando as proporções de sin2θ (indicado como $Q^2$ na segunda tabela) para diferentes picos de difração, a estrutura cristalina e os índices Miller podem ser determinados.
| Plano de cristal (hkl) | $Q^2$ | Treliças espaciais das quais são possíveis reflexos | |||||
|---|---|---|---|---|---|---|---|
| 100 | 1 | SC | |||||
| 110 | 2 | SC | BCC | ||||
| 111 | 3 | SC | FCC | DC | |||
| 200 | 4 | SC | BCC | FCC | |||
| 210 | 5 | SC | |||||
| 211 | 6 | SC | BCC | ||||
| – | 7 | ||||||
| 220 | 8 | SC | BCC | FCC | DC | ||
| 300, 221 | 9 | SC | |||||
| 310 | 10 | 10 | SC | BCC | |||
| 311 | 11 | SC | FCC | DC | |||
| 222 | 12 | SC | BCC | FCC | FCC | ||
| 320 | 13 | SC | |||||
| 321 | 14 | SC | BCC | ||||
| – | 15 | ||||||
| 400 | 16 | SC | BCC | FCC | DC | ||
X-A difração de raios tem uma ampla gama de aplicações para a caracterização de materiais. Pode ser usada como um método experimental para determinar experimentalmente o volume de uma célula unitária para cálculos teóricos de densidade. Adicionalmente, se o material estiver sob tensão residual, a malha distorcida exibirá uma gama de d-spacings que satisfazem a lei de Bragg, resultando em picos de difração muito mais amplos. A largura dos picos de difração também pode ser usada na determinação do tamanho da partícula.