Volta ao Índice de Lições | Fazer as Lições na Ordem | Página de fácil impressão
Matrix Row Operations (página 1 de 2)
“Operações” é matemático-ese para “procedimentos”. As quatro “operações básicas” sobre números são adição, subtração, multiplicação e divisão. Para matrizes, há três operações básicas de linha; ou seja, há três procedimentos que você pode fazer com as linhas de uma matriz.
A primeira operação é comutação de linha. Por exemplo, dada a matriz:

…você pode trocar as linhas para colocar a matriz em uma disposição de linhas mais agradável, como esta:
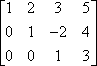
A troca de linhas é muitas vezes indicada pelo desenho de setas, como esta:

Quando trocar as linhas, tenha cuidado para copiar as entradas corretamente.
A segunda operação é a multiplicação de linhas. Por exemplo, dada a seguinte matriz:

…você pode multiplicar a primeira linha por -1 para obter um valor principal positivo na primeira linha:
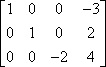
Esta multiplicação de linha é muitas vezes indicada usando uma seta com multiplicação listada em cima, assim:
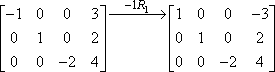
> O “-1R1” indica a operação real. O “-1” diz que multiplicamos por um negativo; o “R1” diz que estávamos a trabalhar com a primeira linha. Note que a segunda e terceira filas foram copiadas para baixo, inalteradas, para a segunda matriz. A multiplicação só se aplicou à primeira linha, portanto as entradas para as outras duas linhas apenas foram levadas inalteradas.
Pode multiplicar por qualquer coisa que quiser. Por exemplo, para obter um 1 na terceira linha da matriz anterior, você pode multiplicar a terceira linha por uma metade negativa:

Desde que você não estava fazendo nada com a primeira e segunda linhas, essas entradas foram apenas copiadas inalteradas para a nova matriz.
Você pode fazer mais de uma multiplicação de linhas dentro do mesmo passo, então você poderia ter feito os dois passos acima em apenas um passo, assim:
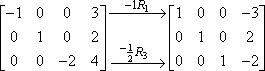 >
>
É uma boa idéia usar alguma forma de notação (como as setas e subscritos acima) para que você possa manter o controle do seu trabalho. As matrizes são muito confusas, especialmente se você as estiver fazendo à mão, e as notas podem facilitar a verificação do seu trabalho mais tarde. Também impressionará o seu professor.
A última operação de linha é a adição de linhas. A adição de linhas é semelhante ao método “adição” para resolver sistemas de equações lineares. Suponha que você tenha o seguinte sistema de equações:
x + 3y = 1
-x + y = 3 Copyright © Elizabeth Stapel 2003-2011 All Rights Reserved
Advertisement
Você poderia começar a resolver este sistema adicionando abaixo as colunas para obter 4y = 4:
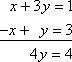
Pode fazer algo semelhante com matrizes.Por exemplo, dada a seguinte matriz:

…você pode “reduzir” (obter mais zeros iniciais) a segunda linha adicionando-lhe a primeira linha (o objectivo geral com matrizes nesta fase é obter um “1” – ou “0’s” e depois um “1” – no início de cada linha da matriz). Quando você estava reduzindo o sistema linear de duas equações ao adicionar, você desenhou uma barra “igual” ao longo do fundo e adicionou para baixo. Quando você estiver usando a adição em uma matriz, você precisará pegar algum papel de raspar, porque você não quer tentar fazer o trabalho dentro da matriz. Então adicione as duas linhas no seu papel de raspar:
|
Trabalho de raspar – |
|
Esta é a sua nova segunda linha; você irá escrevê-la no lugar da segunda linha antiga. O resultado será assim:
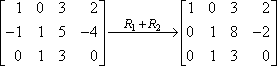
Neste caso, o “R1 + R2” na seta significa “Eu adicionei a linha um à linha dois, e este é o resultado que eu obtive”. Como a linha um não mudou, e como não fizemos nada com a linha três, estas linhas são copiadas para a nova matriz inalteradas.
Top | 1 | 2 | Voltar ao Índice Seguinte >>
|
Cite este artigo como: |
Stapel, Elizabeth. “Matrix Row Operations.” Purplemath. Disponível a partir de 2016
|