X線回折は、結晶方位や原子間距離を同定することができる一般的な材料評価技法です。 X線は、波長が原子間距離や格子定数の値と同じ長さスケールであるため、これに用いられます。
何が起こっているのか?
X線は、真空管内でタングステンフィラメントをその仕事関数以上に加熱し、電子を放出させることによって生成されます。 電子の平均自由行程を大きくするために、真空状態が必要です。 電子は25keVのエネルギーで銅の陰極に加速される。 銅陰極に衝突した電子は内殻電離を起こし、高エネルギーの電子が低エネルギーの空孔を埋めるために降下し、X線を発生させる。 また、様々な高エネルギー準位の電子が落下し、様々なエネルギーの電磁波が発生する。 このようにして、複数の波長(K-β型とK-α型)のX線が発生する。 X線回折では、単色光が試料と相互作用するのが理想的なので、ニッケル板でK-β線のX線はフィルタリングされます。 Kα線のエネルギーは確かに2つありますが、エネルギーが非常に似ているため、全体のピークプロファイルに大きな影響を与えません。 X線はビーム幅を調整するためにコリメータを通過します。
ブラッグの法則の背景
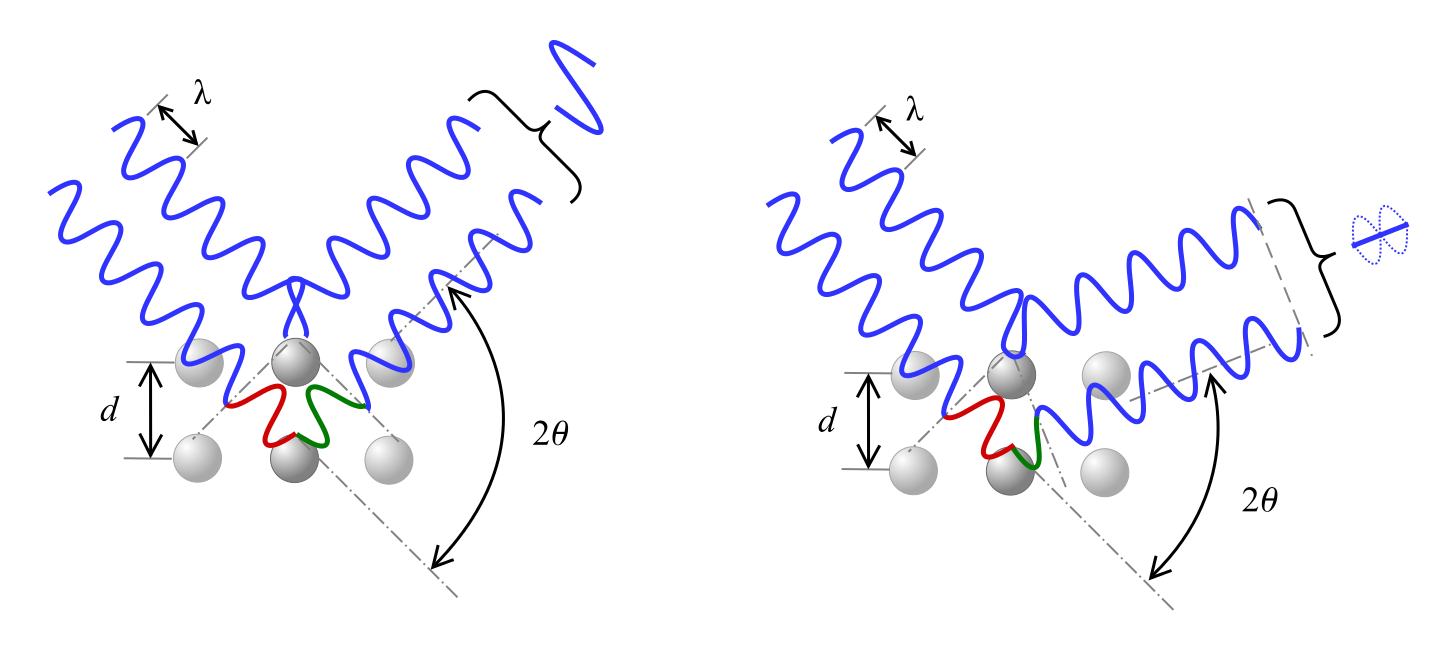
ブラッグの法則は、角度θで材料に入射した波長λのX線が距離dだけ離れた結晶面によって回折される建設的干渉の関係を記述し、nは整数を表しています。
下図に示すように、波の位相がずれると、2θの角度に応じて、左図のような建設的干渉と、右図のような破壊的干渉が起こる。
X線回折の結果を解釈する方程式
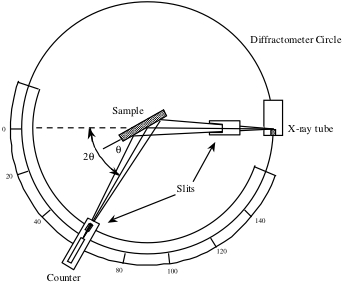
X線回折計の概略図で下に見られるカウンターが、2θ値の範囲内で回転され、各位置で結晶から反射したX線信号強度が記録されます。
ブラッグ条件を満たす角度では、建設的干渉によりX線信号のピークが観測される。 このピークを利用して、結晶の方向を特定し、格子定数を計算する。 立方晶系では、結晶形状から得られる以下の式で平面間距離dを計算できます。aは格子定数、h、k、lはミラー指数です。
ここで、定数をすべて式の左辺に移動させ、異なるピーク間のsin2(θ)の値の比とミラー指数を比較できるようにしました。
入射電磁波がサンプル材料に衝突すると、材料に存在する電子が振動パターンに乱され、新しいX線を生成して入射光波を効果的に散乱させます。 コヒーレント散乱(弾性散乱)とは、振動する電子が密に結合して同じ波長のX線を散乱するもので、インコヒーレント散乱とは、疎に結合した電子が振動運動して異なるエネルギーのX線を発生させるものである。 X線回折は、コヒーレント散乱されたX線の強度を測定するもので、波が建設的に干渉する部分にピークがある。 原子散乱係数は、原子によって散乱される波の振幅を電子1個によって散乱される波の振幅で割った比率として定義することができる。
XRD データの例
以下は、私が学部の実験コースで行った、結晶構造に基づいて未知の金属を特定しようとする実験から収集されたデータです 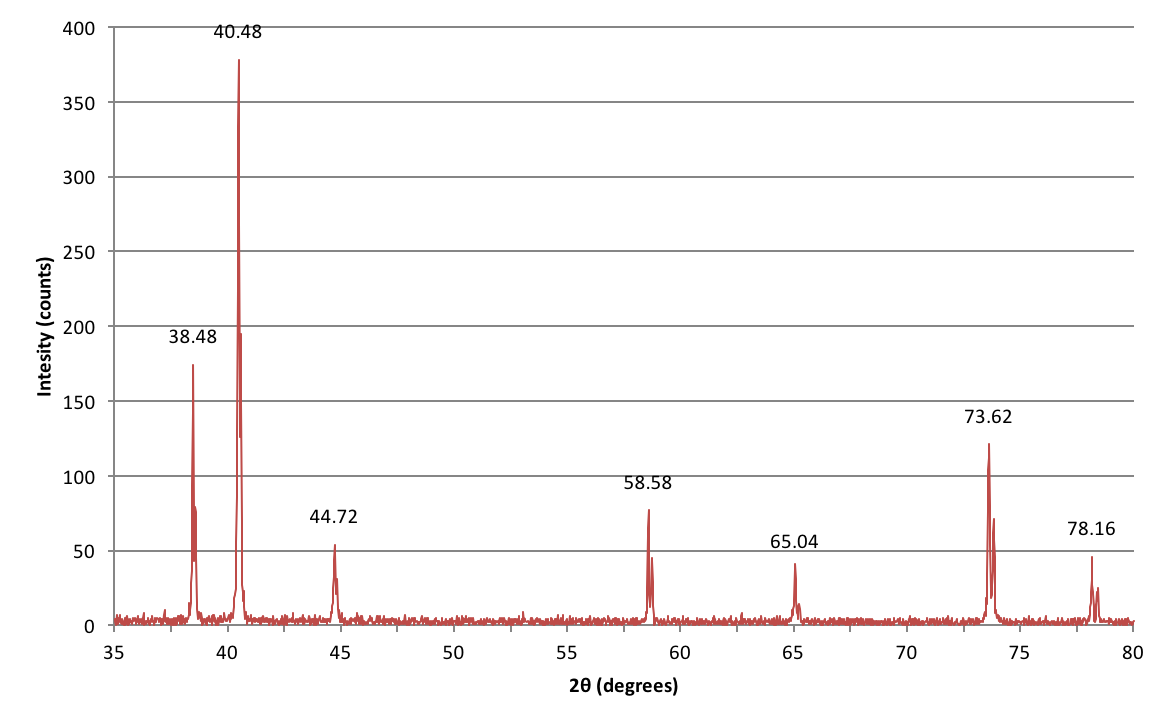
これらのピークはどのように解釈すればいいですか。
| Crystal Structure | Conditions |
|---|---|
| Simple Cubic | all h、k, l 値 |
| Body Centered Cubic | h+k+l は偶数であること |
| Face Centered Cubic | h, k, and l must be all odd or all even |
Structure factorsは、隣接する2面の中間に面が存在し破壊的干渉が起こる場合を考慮したものです。 これらの要因によって、異なる結晶構造形状に対して、いつ建設的干渉が起こるかを決定する一連の規則が生まれます。 上の表は、構成的干渉が発生するミラー指数パラメータを示したものです。 より詳細な表は以下のとおりです。 異なる回折ピークのsin2θ(2番目の表では$Q^2$と表記)の比を比較することで、結晶構造とミラー指数を決定することができます。
| 結晶面(hkl) | $Q^2$ | 反射が可能な空間格子 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 100 | 1 | SC | 110 | 2 | SC | BCC | |||
| 111 | 1103 | sc | fcc | dc | |||||
| 200 | 4 | sc | bcc | fcc | |||||
| 210 | 5 | sc | bcc | fcc | bcc | sc | |||
| 211 | 6 | sc | bcc | ||||||
| – | 7 | ||||||||
| 220 | 8 | sc | bcc | fcc | dc | ||||
| 300のことです。 221 | 9 | sc | |||||||
| 310 | 10 | sc | bcc | ||||||
| 311 | 11 | sc | fcc | dc | |||||
| 222 | 12 | sc | bcc | fcc | |||||
| 320 | 13 | sc | |||||||
| 321 | 14 | sc | bcc | ||||||
| 321 | – | 15 | 16 | sc | bcc | fcc | dc | ||
X->
のように。線回折は、材料の特性評価に幅広く応用されています。 理論的な密度計算のために、単位セルの体積を実験的に決定する方法として使用することができる。 また、材料に残留応力がかかっている場合、歪んだ格子はブラッグの法則を満たす範囲のd-spacingsを示し、回折ピークはより広い範囲になります。 回折ピークの幅は、粒子径を決定する際にも利用されることがあります。