Introduction
コンピュータサイエンスにおいて、無周期の有向グラフ (DAG) はサイクルを持たないグラフであり、このようなグラフのトポロジカルソートを行うことです。 このチュートリアルでは、DAGのトポロジカルソートを線形時間で行う方法を紹介します。
トポロジカルソート
多くのアプリケーションで、我々は事象間の優先度を示すために有向無サイクルグラフを使用しています。 例えば、スケジューリング問題では、タスクの集合とこれらのタスクの順序を指定する制約の集合が存在する。 タスクを表現するために、DAGを構築することができる。 DAGの有向辺はタスクの順序を表す。
人が公式の場で服を着る場合の問題を考えてみよう。 靴下、ズボン、靴など、いくつかの衣服を身につける必要がある。 いくつかの衣服は、他の衣服より先に着なければなりません。 例えば、靴下は靴の前に履かなければなりません。 ある衣服は、靴下とズボンのように、どのような順序でも着ることができる。 この問題を説明するためにDAGを使うことができる。
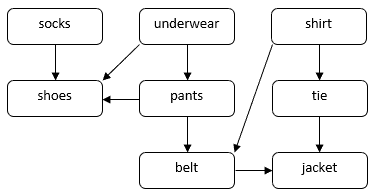
このDAGでは、頂点が衣服に対応している。 DAGの直接辺
は、衣服
の前に衣服
を身につける必要があることを示している。 我々の課題は、依存性制約を考慮しながら、すべての衣服を着る順番を見つけることである。 例えば、以下の順序で衣服を着ることができる：
DAG 
のトポロジカルソートは、そのすべての頂点の線形順序であり、もし に辺 が含まれていれば、順序において は より前に出現することになる。 DAGの場合、実行時間が頂点の数と辺の数に線形な位相的ソートを構築することができ、それは
である。
Kahn’s Algorithm
DAGにおいて、グラフがサイクルを含まないため、2頂点間のどのパスも有限長になる。 8042＞（送信元の頂点）から＜7621＞（送信先の頂点）までの最長経路を＜4879＞とする。 
が最長経路なので、への入射辺は存在し得ない。 したがって、DAGには少なくとも1つ、入射エッジを持たない頂点がある。 Kahn’s Algorithm
Kahnのアルゴリズムでは、入力エッジを持たない頂点を見つけることによってDAGの位相ソートを構築する：
このアルゴリズムでは、まず全ての頂点の内次値を計算し、
次に内次が0で出力リストの最後尾にある頂点から開始する。 頂点を選んだら、その頂点とその外側の辺がグラフから削除されるので、隣接する頂点の内次の値を更新する。
すべての頂点を選ぶまで上記の処理を繰り返せばよい。 出力リストはグラフのトポロジカルソートとなる。 時間複雑度
すべての頂点の内次を計算するために、のすべての頂点と辺を訪れる必要がある。 したがって、インディグリー計算の実行時間はである。 これらの値を再度計算するのを避けるために、これらの頂点の内次の値を追跡する配列を使用することができる。 whileループの中では、すべての頂点と辺を訪問する必要もある。 したがって、全体の実行時間はとなる。
Depth First Search
また、Depth First Search（DFS）アルゴリズムを用いて位相ソートを構築することもできる。
4.1. 再帰によるグラフDFS
DFSでトポロジカルソートの側面に取り組む前に、標準的な再帰的グラフDFSトラバーサルアルゴリズムを確認することから始めましょう：
標準DFSアルゴリズムでは、のランダムな頂点から始めてこの頂点を訪問としてマークします。 その後、dfsRecursive関数を再帰的に呼び出して、その訪問されていない隣接する頂点を全て訪問する。 このようにして、のすべての頂点を時間で訪問できる。
ただし、各頂点を訪問したときにすぐにリストに入れるため、またどの頂点からでも開始できるため、標準DFSアルゴリズムはトポロジカルにソートされたリストを生成することを保証することはできない。 DFSベースのトポロジカルソートアルゴリズム
DAGのトポロジカルソートを生成するために、DFSアルゴリズムを修正することができる。 DFSのトラバーサル中に、頂点のすべての近傍を訪問した後、それを結果リスト
の先頭に置く。 このようにして、がソートされたリストのすべての近傍の前に現れることを確認できる：
このアルゴリズムは、標準DFSアルゴリズムに似ている。 相変わらずランダムな頂点から始めるが、一度訪れた頂点をすぐにリストに入れることはしない。 その代わり、まずその近傍の頂点を再帰的にすべて訪問し、それからその頂点をリストの先頭に配置します。 したがって、がエッジを含む場合、はの前に現れる。
全体の実行時間もであり、DFSアルゴリズムと同じ時間複雑性を持つ。
まとめ
この記事では、DAGに対する位相ソートの一例を紹介した。 また、時間でトポロジカルソートを行うことができる2つのアルゴリズムについて説明した。
DFSベースのトポロジカルソートアルゴリズムのJava実装は、Javaでの深さ優先探索の記事で利用可能である。