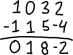レッスンインデックスに戻る|レッスンを順番に行う|印刷用ページ
Matrix Row Operations (page 1 of 2)
「オペレーション」は数学者語で「手順」の意味です。 数に対する「基本操作」は、足し算、引き算、掛け算、割り算の4つです。 つまり、行列の行に対して行うことができる 3 つの手順があります。
最初の操作は行の入れ替えです。 例えば、

…という行列があったとします。行の入れ替えは、次のように矢印で示されることがよくあります。 例えば、次のような行列があるとします:

…。1153>
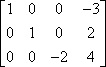
この行の乗算は、しばしば次のように乗算が上に記載された矢印を使って示されます:
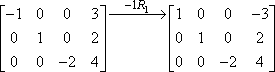
「-1R1」は実際の操作を示します。 1」はマイナス1乗を意味し、「R1」は1行目の演算を意味する。 2行目と3行目は、変更されずに2番目の行列にコピーされたことに注意してください。 乗算は最初の行にのみ適用されるので、他の 2 行のエントリは変更されずにそのまま運ばれました。
好きなように乗算することができます。 たとえば、前の行列の 3 行目の先頭の 1 を取得するには、3 行目に負の 2 分の 1 を掛けます。

1 行目と 2 行目は何もしていないため、これらのエントリは新しい行列にそのままコピーされました。
同じステップ内で複数の行の乗算を行うことができるので、上記の 2 つのステップを次のように 1 つのステップで行うことができます。 行列は特に手書きでやっていると非常に面倒ですし、メモがあれば後で自分の作業を確認しやすくなります。 また、先生の印象にも残ります。
最後の行の演算は、行の追加です。 行加算は連立方程式の解法である「足し算」に似ています。 次の連立方程式があるとします:
x + 3y = 1
-x + y = 3 Copyright © Elizabeth Stapel 2003-2011 All Rights Reserved
Advertisement
あなたはこのシステムを、4y = 4になる列を下に追加することから解くことができました。
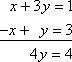
行列でも同じようなことができます。例えば、次の行列があるとします:

…最初の行を追加することによって、2行目を「減らす」(先頭の0を増やす)ことができます(この段階での行列の一般目標は、各行頭で「1」-または「0」-そして「1」を取得することです)。 2方程式の連立方程式を足し算で減らすとき、下に「イコール」の棒を引いて下に足していきましたね。 行列で足し算をするときは、スクラッチ紙が必要です。行列の中で作業をするのは嫌だからです。
|
Scratch work – |
|
This is your new second row; you will write it in place of the old second row.これは、あなたが新しく書いた行の2行目。 結果は次のようになります。
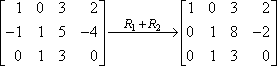
この場合、矢印の「R1 + R2」は「1行目を2行目に足したら、こういう結果になりましたよ」という意味です。 1行目は実際には変化しておらず、3行目には何もしていないので、これらの行は変化せずに新しい行列にコピーされます。
トップ|1|2|インデックスに戻る 次へ >>
|
この記事の引用元: |
ステープル,エリサベス. “行列の行の操作” Purplemath. 2016
|
.