Prequisite – Graph Theory Basics – Set 1
グラフとは、ある意味において「関連」を持つ対象の集合に相当する構造のことである。 グラフの対象は頂点に対応し、それらの間の関係は辺に対応する。 グラフは頂点を表す点と辺を表す線または曲線で結ばれており、図式的には
「グラフ
は頂点（またはノード）の空でない集合
と辺の集合
からなる。 グラフの種類：グラフにはいくつかの種類があり、辺の数、方向、重さなどによって区別される
1. 単純グラフ – 各辺が2つの異なる頂点を結び、2つの辺が同じ頂点の組を結ばないグラフを単純グラフという。 例えば、次のようなグラフを考えてみましょう。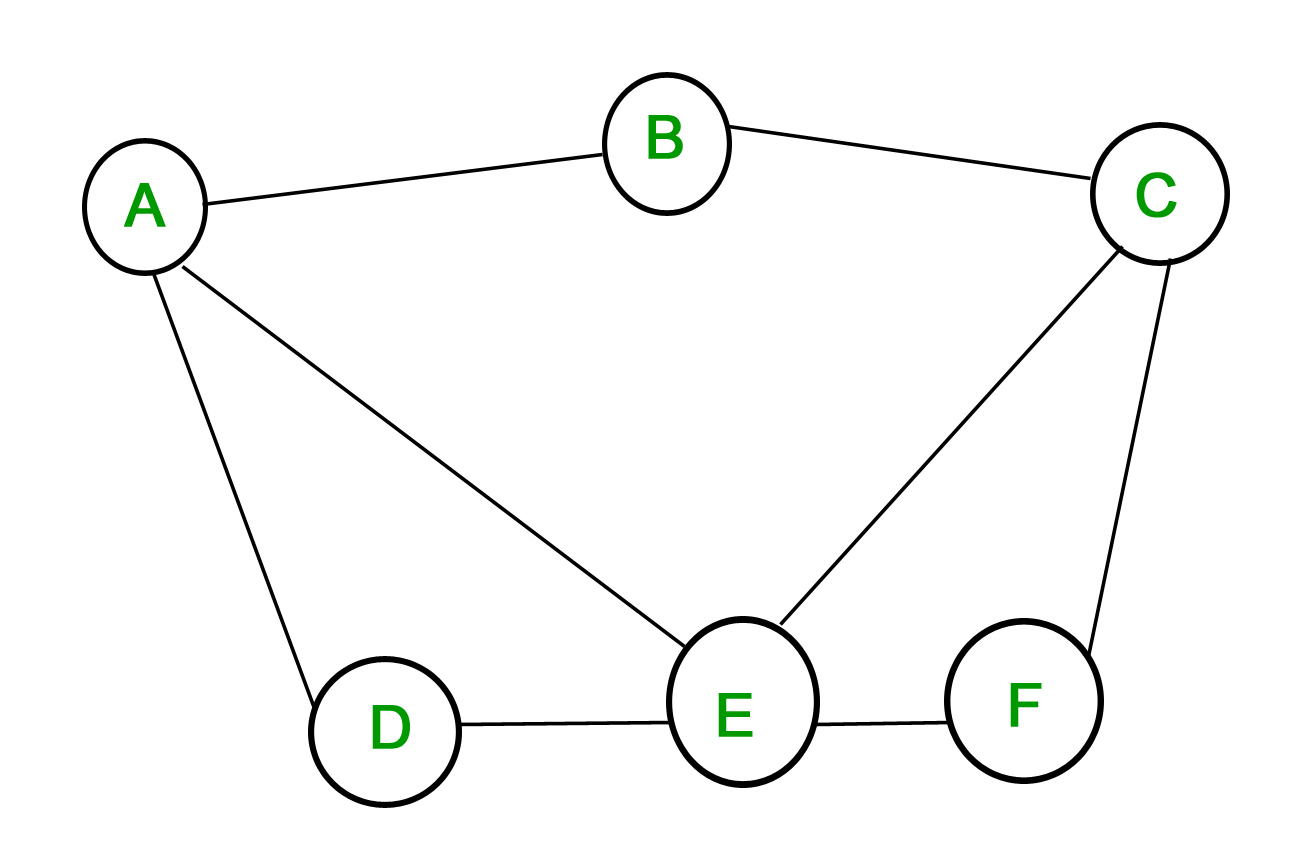
上のグラフは、自己ループを持つ頂点がなく、2つ以上の辺がつながっている頂点がないので、単純グラフです。
辺は、それがつなぐ頂点で示されます。
は頂点
と
をつなぐ辺。
2. 5935>
上のグラフはと
の間に複数の辺があるのでマルチグラフと呼ばれる。 エッジ
の多重度は2です。
上に示したグラフとは異なり、エッジが有向なグラフもあります。 これはオブジェクト間の関係が双方向ではなく、一方通行であることを意味する。 用途によっては辺の方向が重要な場合もある。
辺が有向か無向かによって、有向グラフと無向グラフがあります。 この性質を単純グラフや多グラフに拡張して、有向または無向の単純グラフ、有向または無向の多グラフを得ることができる。
グラフの基本用語：
以上の説明で、頂点、辺、有向辺、無向辺などグラフに関するいくつかの用語がすでに説明されている。 7805>
- 隣接度 – グラフ
において、2つの頂点
と
が辺の端点である場合、隣接しているという。 辺
は頂点に入射するという。
辺が有向の場合、はに隣接するといい、はから隣接するという。 ここでを始点、を終点という。 - Degree – 頂点の次数は、頂点の次数に2倍寄与する自己ループを除いて、その頂点に付随する辺の本数である。 頂点の次数 は
.
である。有向グラフの場合、次数はさらに内次と外次に分類される。 頂点のイン度は、与えられた頂点を終点とする辺の数である。 また、頂点の外延度は、与えられた頂点を始点とする辺の数である。 イン度は
、アウト度は
と表記する。
例えば、都市間のフライトを描いた上の有向グラフでは、頂点「デリー」のイン度は3、アウト度も3である。
注：頂点の次数が0だと孤立と呼ばれる。
Handshaking Theorem :
グラフのすべての頂点の次数を足すとどうなるか。 無向グラフの場合、各辺は2回寄与し、1回目は始点、2回目は終点に寄与する。 したがって、次数の和は辺の数の2倍になる。 この事実は「握手の定理」で述べられている。
Let be an undirected graph with edges. ThenIn case G is a directed graph,
The handshaking theorem, for undirected graphs, has a interesting result –
An undirected graph has an even number of vertices of odd degree.
Proof : 
と
をそれぞれ偶数と奇数度の頂点の集合とする。
握手定理により、
だから、
偶数度を持つ頂点の度の和は偶数であることがわかる。 LHSも偶数なので、奇数度の頂点の度数の和は偶数でなければならない。
したがって、奇数度の頂点の数は偶数である。
Some special Simple Graphs :
1. 完全グラフ – 
頂点の単純グラフで、各頂点の組の間にちょうど1本の辺があるものを完全グラフという。 5598個の頂点を持つ完全グラフは 
で表される． 完全グラフの頂点がn個で辺の総数がn*(n-1)/2である。 サイクル – サイクルは頂点が
で辺が
の単純なグラフである． 頂点が個のサイクルは
と表記される。 7805>
3. 輪 – 輪はサイクルに似ているが、他のすべての頂点に接続する頂点が1つ追加されたものである。 5598個の頂点に1個の頂点を加えたものを
と表記する。 5935>
4. ハイパーキューブ – ハイパーキューブまたはnキューブは、
個の頂点がそれぞれnビットの文字列で表されるグラフである。 最大でも1ビットしか違わない頂点は辺で結ばれる。 個の頂点を持つハイパーキューブは
と表記される。
5.キューブグラフの個の頂点を持つ辺の総数はn*
個である。 2部グラフ – 単純グラフの頂点集合を2つに分割し，のすべての辺の始点が第1集合に，終点が第2集合にあるとき，2部グラフという．
定理 – 単純なグラフは、グラフの各頂点に
異なる2色のうちの1色を割り当てて、隣り合う2色が
同じ色にならないことが可能である場合にのみ二部構成となる。
2つの不連続な部分集合に
個と個の頂点を持つ2-部グラフは， 第1集合のすべての頂点から第2集合のすべての頂点へ， 合計
個の辺があれば完全と言うことができる． 第一集合に個の頂点、第二集合に個の頂点を持つ完全二部グラフを
と表す。
GATE CS Corner Questions
以下の問題を練習すると、自分の知識を試すのに役に立つ。 すべての問題は、過去のGATEで、あるいはGATE Mock Testsで出題されたものです。 練習することを強くお勧めします。
1. GATE CS 2013、問題25
2.GATE CS 2014 Set-1、問題61
3.GATE CS 2006、問題71
4.GATE CS 2002、問題25
5.GATE CS 2013、問題2
6.GATE CS 2013、問題3
7.GATE CS 2014、問題4
8. GATE CS 2004, Question 37
6. GATE CS 2014 Set-2, Question 13
参考文献-
Graphs – Wikipedia
Discrete Mathematics and its Applications, by Kenneth H Rosen
この記事はChirag Manwani氏によって寄稿されています。 GeeksforGeeks が好きで寄稿したい方は、contribute.geeksforgeeks.org を使って記事を書いたり、[email protected] に記事を郵送することもできます。 あなたの記事が GeeksforGeeks のメインページに表示され、他の Geeks を助けることができます。