- 接続性は、グラフ理論の基本概念である。 グラフが接続されているか、切断されているかを定義する。 接続性がなければ、ある頂点から別の頂点へグラフをたどることはできない。
- グラフは、すべての頂点のペアの間にパスがある場合、接続グラフという。 すべての頂点から他のどの頂点へも横断する道があるはずである。 これはグラフの連結性と呼ばれる。
- グラフが切断されている頂点と辺が複数存在する場合、グラフは切断されているという。
- グラフの連結性理論はネットワークアプリケーション、ルーティング輸送ネットワーク、ネットワーク耐性などに不可欠である。 ここでは、B -> A -> D -> F -> E -> Hという経路で頂点BからHまでたどることができるので、連結グラフになります。
Cut Vertex
グラフを切断する1つの頂点をカットバーテックスと呼ぶ。
Gを連結グラフとする。 Gの頂点vは、G-v (Remove v from G)の結果、切断されたグラフになるとき、Gのカット頂点と呼ばれる。
グラフから頂点を取り除くと、グラフは2つ以上のグラフに分かれる。
注:Gをn個の頂点を持つグラフとする:
- 連結グラフGは最大(n-2)個の切断頂点を持つことがある:
- 切断頂点を取り除くとグラフが切断されたままになるかもしれない。
- 頂点を削除すると、グラフの構成要素の数が少なくとも1つ増える。
- 木の非ペンダント頂点はすべてカット頂点である。
例1

例2
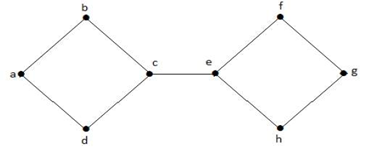
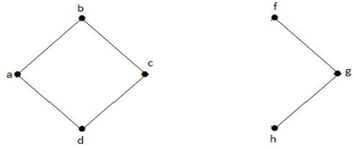
上のグラフで頂点 ‘e’ はカット頂点である。
カットエッジ(ブリッジ)
カットエッジまたはブリッジとは、その除去によってグラフが切断される1本の辺のことである
Gを連結グラフとする。 Gの辺eは、G-e(Gからeを取り除く)が切断されたグラフになるとき、Gのカット・エッジと呼ばれる。
あるグラフから辺を取り除くと、グラフは2つ以上のグラフに分かれる。
注:Gをn個の頂点を持つグラフとする:
- 連結グラフGは最大で(n-1)個のカットエッジを持つことがある:
- カットエッジを取り除くとグラフが切断されたままになることがある。
- 辺を削除すると、グラフの構成要素の数は最大でも1つ増える。
- 切断辺 ‘e’ はGのどのサイクルにも含まれてはならない。
- 切断辺の少なくとも1頂点は切断頂点であるので、切断辺が存在すれば、切断頂点もまた存在するはずである。
- カットされた頂点が存在するならば、どんなカットエッジも存在する必要はない。
例1
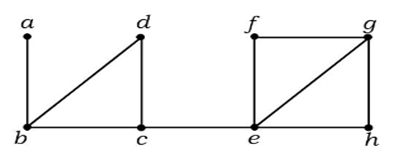
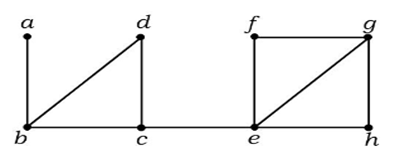
上のグラフで、エッジ (c, e) がカットエッジである。
例2
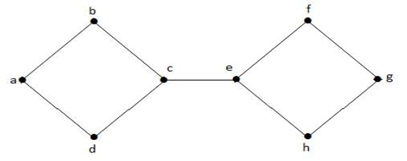
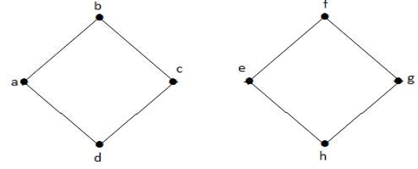
上のグラフで、辺(c, e)はカットエッジである。
Cut Set
連結グラフGにおいて、カットセットとは次の性質を持つ辺の集合Sである:
- Sの辺を全て削除するとGは切断される。
- Sの中のいくつかの辺(全てではない)を削除してもGは切断されない。
例1
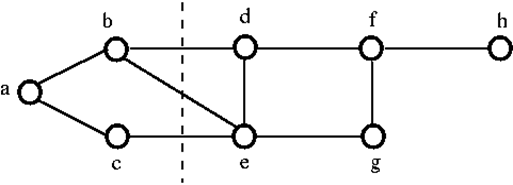
上のグラフGを切断するには、3つの辺、すなわちbd, be, ceを削除しなければならない。 つの辺のうち2つだけを取り除いても切断することはできない。 したがって、{bd, be, ce}は切断集合である。
上のグラフから切断集合を取り除くと、次のようになる:
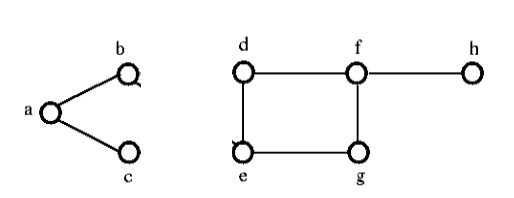
Edge Connectivity
連結グラフGの辺結合度は、取り除くことによってGが切断される辺の最小数である。
λ(G)≧kのとき、グラフGはk-edge-connectedと呼ばれる。
例題
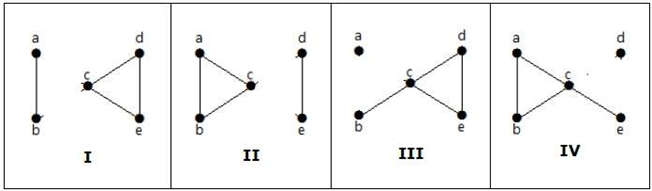
上のグラフから、最小辺を2本取り除くと、連結グラフが不連結グラフになることを見てみよう。 したがって、その辺の結合度は2であり、上のグラフは2辺結合グラフである。
2つの辺を削除してグラフを切断する方法は次の4通りある:
Vertex Connectivity
連結グラフGの結合度(または頂点の結合度)は、削除によってGが切断またはトリビアグラフに縮小する頂点の最小個数である。 K(G)で示される。
グラフはK(G)≧kのとき、k-連結またはk-頂点連結という。
例
例を見てみよう。
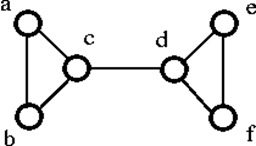
上のグラフGはcかdのどちらか1つの頂点を削除すれば不連結になることがわかる。 したがって、その頂点の接続性は1であり、1-connected graphである。