線形判別分析の説明

判別分析による分類

LDAが教師あり分類法としてどのように導かれるかを見てみましょう。 一般的な分類問題を考えてみよう： 確率変数XはK個のクラスの1つに由来し、いくつかのクラス固有の確率密度f(x)がある。 判別ルールは、データ空間をすべてのクラスを表すK個の不連続な領域（チェス盤の箱を想像してください）に分割しようとします。 この領域があれば、判別分析による分類は、xが領域jにあればクラスjに振り分けられるということになる。 329>

• 最尤法：各クラスが等しい確率で出現すると仮定すると、

• Bayesian rule.であればxをjクラスに割り当てることができる。 クラスの事前確率πがわかっている場合、xをクラスjに割り当てる

Linear and quadratic discriminant analysis

多変量のガウス分布からデータが来るとする、つまり、ガウス分布の場合は。すなわち、Xの分布がその平均(μ)と共分散(Σ)で特徴付けられるとすると、上記の配分規則の明示的な形が得られます。 ベイズ則に従い、データxをクラスjに分類するのは、i＝1，…，K：

上の関数は判別関数と呼ばれます。 ここでは対数尤度を用いていることに注意。 つまり、判別関数はデータxが各クラスからどれだけの確率で出ているかを教えてくれるのです。 したがって、任意の2つのクラスkとlを分ける判定境界は、2つの判別関数が同じ値を持つxの集合となる。 したがって、決定境界上にあるデータは、2つのクラスからの可能性が等しい（決められない）ことになる。

LDAは、Kクラス間の共分散が等しいと仮定した場合に発生するものである。 つまり、クラスごとに共分散行列が1つではなく、すべてのクラスが同じ共分散行列を持つ。 このとき、次のような判別関数が得られます：

これがxの線形関数であることに注意してください。したがって、任意のクラスの組間の決定境界もxの線形関数となり、線形判別分析と名付けられた理由でもあるのです。 等共分散の仮定がなければ、尤度の2次項は相殺されないので、得られる判別関数はxの2次関数となります。

このとき判別界はxに対して2次関数になっていることがわかります。 これは2次判別分析(QDA)として知られています。

どちらが良いですか。 LDAかQDAか？

実際の問題では、母集団のパラメータは通常未知で、訓練データからサンプル平均とサンプル共分散行列として推定されます。 QDAはLDAに比べてより柔軟な決定境界に対応できるが、推定に必要なパラメータ数もLDAより早く増加する。 LDAの場合、(2)の判別関数を構成するために(p+1)個のパラメータが必要である。 K個のクラスがある問題では、1個のクラスを任意に選んで基底クラスとする（基底クラスの尤度を他の全てのクラスから引く）ことで、このような判別関数は（K-1）個で済むことになる。 したがって、LDAの推定パラメータ総数は(K-1)(p+1)となる。

一方、(3)のQDA判別関数それぞれについて、平均ベクトルと共分散行列、クラス事前分布が推定される必要がある。
– 平均: p
– 共分散: p(p+1)/2
– クラス事前分布: 1
同様に、QDAでは、(K-1){p(p+3)/2+1}個のパラメータを推定する必要がある。

そのため、LDAのパラメータ推定数はpに対して線形に増加し、QDAのそれはpに対して2次関数的に増加します。問題の次元が大きい場合、QDAはLDAよりも性能が悪くなると予想されます。 LDA & QDA

個々のクラスの共分散行列を正則化することで、LDAとQDAの間の妥協点を見つけることができます。 正則化とは、推定されるパラメータにある種の制限をかけることである。 この場合、個々の共分散行列がペナルティ・パラメータを通じて共通のプールされた共分散行列に向かって縮小することを要求する、例えば、α：

また、共通共分散行列はペナルティ・パラメータを通じて例えば恒等行列に向けて正規化することが可能である。 β:

入力変数の数がサンプル数を大きく上回る状況では、共分散行列はうまく推定できない可能性があります。 縮小はうまくいけば推定と分類の精度を向上させることができます。 これは、下の図で説明されています。

LDAの計算

（2）と（3）から、共分散行列を先に対角化すれば、判別関数の計算を簡単にできることが分かる。 つまり、共分散行列が恒等行列（相関なし、分散1）になるようにデータを変換するのである。 LDAの場合、計算の進め方は以下の通りです。

ステップ2はデータを球面化して変換後の空間における等値共分散行列を生成する。 ステップ4は(2)に従って得られる。

LDAが実際に何をしているかを見るために、2クラスの例を挙げてみよう。 kとlの2つのクラスがあるとします。xをクラスkに分類するのは、

上の条件はクラスkがクラスlよりデータxを生成しやすいということです。 以上の4つのステップに従って、

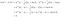
と書く。 データxをクラスkに分類するのは、

このように導かれた配分規則から、LDAの働きが見えてくる。 式の左辺（l.h.s.）は、2つのクラス平均を結ぶ線分へのx*の直交射影の長さである。 右辺は、クラスの事前確率で補正された線分の中心の位置である。 基本的には、LDAは散布されたデータを最も近いクラス平均に分類する。 ここで2つの観察ができる：

1. クラス事前確率が同じでないとき、決定点は中間点からずれる、つまり境界は事前確率の小さいクラスに向かって押される。
2. データはクラス平均によって広がる空間に投影される（x*の乗算とルールのl.h.s上の平均値の減算）。 そして距離の比較はその空間で行われる。