Chemical Kinetics
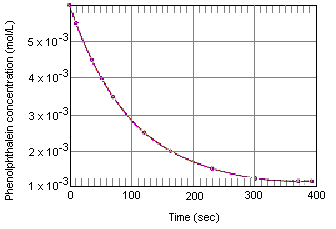
フェノールフタレインを終点指示薬とする酸塩基滴定はよく知られています。 しかし、過剰の塩基の存在下でフェノールフタレインを含む溶液を数分間放置したときに何が起こるか、お気づきでない方もいるかもしれません。 下の表は、フェノールフタレインが0.005M、OH-イオンが0.61Mの溶液で、フェノールフタレインの濃度がどう変化したかを示したもので、最初はピンク色の溶液ですが、フェノールフタレインとOH-イオンが反応して次第に無色になっていきます。 これらのデータを下のグラフにプロットするとわかるように、フェノールフタレイン濃度は約4分間で10分の1に減少しています。
Phenolphthalein と ExcessBase の反応の実験データ
上表のようなデータは、化学動力学（ギリシャ語で「動く」の意）の測定と分類される。
反応速度という用語は、単位時間あたりに起こる量の変化を表すのによく使われます。 例えば、インフレ率とは、標準的な品物の集まりの1年あたりの平均的なコストの変化である。 物体が空間を移動する速度は、単位時間当たりの移動距離で、マイル/時やキロメートル/秒のような単位時間当たりの移動距離である。 化学反応速度論では、移動距離は反応の構成要素の1つの濃度の変化である。 したがって、反応の速度は、与えられた時間
tの間に起こる反応物(X)
の濃度の変化である。
練習問題1：
上の表のデータを使って、次の各期間中にフェノールフタレインがOH-イオンと反応する速度を計算せよ：
(a) 最初の時間間隔で、フェノールフタレインの濃度が0.0050 M から 0.0045 Mまで低下したとき。
(b) 2番目の時間間隔では、濃度が0.0045 Mから0.0040 Mに低下するとき。
(c) 3番目の時間間隔では、濃度が0.0040 Mから0.0035 Mに低下するとき。
練習問題1の答えを確認するには、ここをクリックしてください。
練習問題1の解答はこちら
反応の瞬時速度と反応速度則
フェノールフタレインとOH-イオン間の反応速度は一定ではなく、時間とともに変化します。 ほとんどの反応と同様に、この反応の速度は反応物質が消費されるにつれて徐々に減少する。 つまり、測定している間に反応速度が変化してしまうのです。
これが測定にもたらす誤差を最小にするには、反応が起こるまでの時間に比べて短い時間で反応速度を測定することが望ましいようです。 たとえば、限りなく短い時間tの間に起こる限りなく小さな濃度変化d(X)を測定しようとするかもしれない。
任意の瞬間の反応速度は、反応物（または生成物）の濃度と時間とのグラフから計算することができる。 下のグラフはフェノールフタレインの分解の反応速度が濃度対時間のグラフからどのように計算されるかを示している。 任意の時点における反応速度は、その時点でこの曲線に引かれた接線の傾きに等しい。
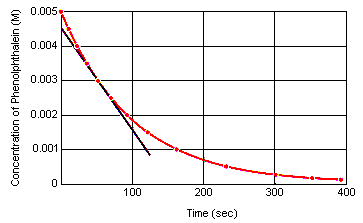
瞬時反応速度は反応物を混合してから反応が平衡に達するまでの任意の時間に測定することができる。
速度則と速度定数
前節のグラフの曲線上のいろいろな点での瞬間反応速度を計算すると面白い結果が得られます。
Rate = k(phenolphthalein)
この式は反応速度を記述する実験則であるので、反応の速度則と呼ばれる。 比例定数kは速度定数と呼ばれる。
練習問題2：
フェノールフタレインの濃度が0.0025Mのとき、瞬時の反応速度が1リットル当たり2.5×10-5モル/秒であるとき、フェノールフタレインとOH-イオンとの反応に対する速度定数を計算せよ
練習問題2に対する答え合わせはこちら
練習問題2の解決法はこちら
練習問題の答えは？
練習問題3：
フェノールフタレインとOH-イオンとの反応の速度定数を用いて、前の表に示した実験データの最初の瞬時反応速度を計算しなさい。
練習問題3の解答はこちら
反応速度の表現方法の違い
反応速度を測る方法は通常1つだけではありません。 たとえば、ヨウ化水素の分解を調べるには、次の反応でH2またはI2が生成する速度、あるいはHIが消費される速度を測定します。
2 HI(g) H2(g) + I2(g)
実験的に、I2が生成する速度が任意の時点のHI濃度の二乗に比例することがわかりました。
H2が生成される速度を調べるとどうなるでしょうか。平衡式から、H2とI2がまったく同じ速度で生成されなければなりません。
しかし、この反応でHIが消費される速度を調べるとどうでしょう。 HIが消費されるのですから、その濃度の変化は負の数になるはずです。 慣例として、反応速度は常に正の数で報告されます。 したがって、反応で消費される物質については、反応速度を報告する前に符号を変更する必要があります。
負の符号は2つのことを行います。 数学的にはHIの濃度における負の変化を正の反応速度に変換する。
H2またはI2の生成をモニターして得られる反応速度と、HIの消失をモニターして得られる速度との間にはどのような関係があるのでしょうか。 反応の化学量論によると、H2またはI2が1分子生成するごとにHIが2分子消費される。 つまり、HIの分解速度は、H2やI2ができる速度の2倍である。 この関係を数式にすると、次のようになります。
その結果、この反応でH2とI2が生成する速度を調べて得られる速度定数（k）は、HIが消費される速度を調べて得られる速度定数（k’）と同じにはならない
練習問題4：
次の反応でI2を生成している瞬間のHIの消滅する速度を計算せよ1。8×10-6モル/リットル・秒：
2 HI(g) 
H2(g) + I2(g)
練習問題4の答え合わせはこちら
練習問題4の答え合わせはこちら
練習問題4の答え合わせはこちら 練習問題4の答え合わせはこちら
練習問題4の答え合わせはこちら
練習問題4の答え合わせはこちら
練習問題5の答え合わせはこちら
The Rate Law Versus the Stoichiometry of a Reaction
1930年代、ロンドン大学のクリストファー・インゴールド卿と共同研究者は、次のような置換反応の動力学を研究しました。
CH3Br(aq) + OH-(aq)
CH3OH(aq) + Br-(aq)
彼らはこの反応の速度が両方の反応物の濃度に比例することを発見しました。
Rate = k(CH3Br)(OH-)
少し異なる出発物質で同様の反応をさせたところ、同様の生成物が得られました。
(CH3)3CBr(aq) + OH-(aq) (CH3)3COH(aq) + Br-(aq)
しかし今度は反応速度が反応物の一方の濃度に比例した。
Rate = k((CH3)3CBr)
この結果から、重要なことがわかる。 反応速度律は反応の化学量論から予測することはできず、実験的に決定されなければならない。 時には、速度法則は反応の化学量論から予想されるものと一致することもあります。
2 HI(g) Rate = k(HI)2
多くの場合、その反応速度は、その反応の化学量論から予想されるものと一致している。 しかし、そうではありません。
| 2 N2O5(g) 4 NO2(g) + O2(g) |
Rate = k(N2O5) |
分子順
1段階で起こる反応もある。 ClNO2からNOに塩素原子が移動してNO2とClNOが生成する反応は一段階反応の良い例です。
ClNO2(g) + NO(g)
他の反応は個々のステップで発生するものもあります。 例えば、N2O5は3段階の機構でNO2とO2に分解される。
| ステップ1： | N2O5 NO2 + NO3 |
| ステップ2: | NO2 + NO3 NO2 + NO + O2 |
| Step 3: | NO + NO3 2 NO2 |
反応の段階は、消費される分子の数を表す分子性で分類される。 消費される分子が1つの場合、その段階は単分子と呼ばれる。 2つの分子が消費される場合は、2分子と呼ばれる。
練習問題5：
N2O5がNO2とO2に分解する反応の各段階の分子量を求めよ。
練習問題5の答え合わせはこちら
練習問題5の解答はこちら
反応は順序で分類することもできる。 N2O5の分解は、反応速度がN2O5の1乗に依存するので1次反応である。
Rate = k(N2O5)
HIの分解は、反応速度がHIの2乗濃度に依存するので、2次反応である。
Rate = k(HI)2
反応速度が複数の試薬に依存する場合、各試薬の順序で反応を分類する。
練習問題6：
NOとO2が反応してNO2を生成する反応の順序を分類せよ：
2 NO(g) + O2(g) 2 NO2(g)
この反応に次の速度則を仮定する：
Rate = k(NO)2(O2)
練習問題6の答えを確認するにはここをクリックして下さい。
反応の分子性と次数の違いは重要である。 反応の分子性、または反応の中の段階は、分子レベルで何が起こるかを説明します。 反応の順序は、巨視的なスケールで何が起こるかを説明します。 私たちは、反応の生成物が現れたり、反応物が消えたりするのを見ることによって、反応の順序を決定します。
Collision Theory Model of Chemical Reactions
The collision theory model of chemical reactions can be used toexplain the rate law for observed both one-step and multi-step reactions. このモデルは、反応のどの段階の速度も、その段階に関与する粒子間の衝突の頻度に依存すると仮定する。
下図は、次のような単純な1段階反応に対する衝突理論モデルの意味を理解するための基礎を提供するものである。
ClNO2(g) + NO(g) NO2(g) + ClNO(g)
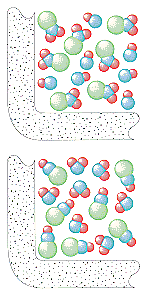
運動分子論は、気体の1秒あたりの衝突回数が1リットルあたりの粒子数に依存すると仮定している。
Rate = k(ClNO2)(NO)
衝突理論モデルは、反応における任意のステップの速度は、そのステップで消費される試薬の濃度に比例することを示唆しています。 したがって一段階反応の速度則はその反応の化学量論と一致するはずである。
たとえば次の反応は一段階で起こる。
CH3Br(aq) + OH-(aq) CH3OH(aq) + Br-(aq)
これらの分子が正しい向きで衝突すると、OH-イオン上の非結合電子1対が下図のようにCH3Br分子の中心にある炭素原子に供与されることができる。
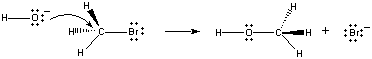
このとき、炭素-臭素結合が切れると同時に、炭素-酸素結合が形成されます。 この反応の結果、OH-イオンがBr-イオンに置き換わります。 この反応は2つの反応物の衝突を伴うsinglestepで起こるので、この反応の速度は両方の反応物の濃度に比例する。
Rate = k(CH3Br)(OH-)
すべての反応が1つのステップで起こるとは限らない。
(CH3)3CBr(aq) + OH-(aq) (CH3)3COH(aq) + Br-(aq)
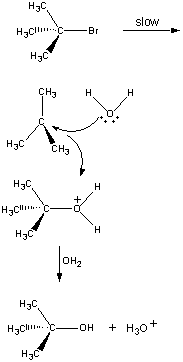
第一段階では(CH3)3CBr分子は一対のイオンへ解離している。
| 第1段階 |  |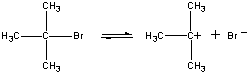
正電荷を持つ(CH3)3C+イオンが第2段階として水と反応します。
| 第二段階 |  |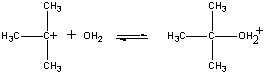
この反応の生成物は最終段階でOH-イオンか水にプロトンを奪われる。
| 第三段階 |  |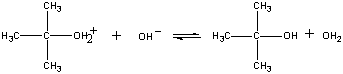
この反応の第二、第三段階は第一段階より非常に速いです。
| (CH3)3CBr (CH3)3C+ + Br-。 |
スローステップ |
| (CH3)3C+ + H2O (CH3)3COH2+ |
ファーストステップ |
| (CH3)3COH2+ + OH-」となる。 (CH3)3COH + H3O |
ファーストステップ |
したがって、全体の反応速度は最初のステップの速度とほぼ同じである。 したがって、最初の段階は、文字通り反応の生成物が形成される速度を制限するため、この反応における律速段階と呼ばれます。
Rate = k((CH3)3CBr)
したがって、この反応の速度法則は、反応の化学量論から予測されるものとは異なっている。
化学反応の速度法則は、次の一般的な規則で説明することができます。
反応における任意の段階の速度は、その段階で消費される試薬の濃度に直接比例します。
ある反応の全体的な速度法則は、反応物が反応の生成物に変換される一連のステップ、またはメカニズムによって決定されます。
ある反応の全体的な速度法則は、その反応で最も遅いステップの速度法則によって支配されています。