円は何面ありますか？

小学校の宿題で、ベテランの数学者の間でも意見が分かれる問題だそうです。 正解を見つけるために、私は最も厳密な科学的手段である Twitter の投票を呼びかけました：

振り返ってみると、「上記のどれでもない」という選択肢を含めなかったことを後悔していますが、それについては後で詳しく説明します。 この投稿では、これらの 3 つの回答 (および「該当なし」) を見ていき、私が考える長所と短所を議論した後、正しい回答を劇的に明らかにします。

しかし最初に、なぜ正しい回答をストレートに示すことができないのでしょうか。 問題文の言葉は、ほとんど神秘的ではありません。 円」とは何か、「いくつ」と数えるのはどういうことか、「辺」とは何か……みんな知っているのではないでしょうか。 以下は、この質問を受けた2人の小学生との議論から得た（大まかな）定義です：

1. 平面図形の図形の境界の一部を形成する線。

ここで「図形」ではなく「平面図形」と言った目的は、2次元で生きる図形（例えば、四角や円、ただし球や立方体は除く）を求めているからである。 次の問題は、定義1の「線」とは何かということです。 Google で “define: side” と入力すると、最も関連性の高い定義は次のようになります：

直線的な図形とは、直線で構成された図形を指します。 つまりこの定義は、定義2をさらに洗練させたもので、正方形が4つの辺を持つことは肯定できますが、円のような非直線的な平面図形については何も言っていません。

Infinitely Many Sides?

私のTwitter投票の回答者は、全国平均よりも高い数学教育レベルを持っていると考えて間違いないでしょう。 この質問で意見が分かれたという事実、そして、この質問の通常の対象者（小学生）にはほとんど利用できない答えを選択した少数派という事実は、確かに何かがどこかで間違っていることを示唆しています。 円は、n が大きくなるにつれて n 辺の多角形の極限であると考えるのは、確かに有効です。 これはまさにアルキメデスや劉輝、その他数え切れないほどの人々が、何世紀にもわたって円形幾何学を研究し、πの近似値を導き出してきたアプローチです。

円は無限に多くの辺を持つ多角形のようなものだと考えるのは、便利な省略表現として絶対に理にかなっている場合があります。

しかし、数学者である堪らない女衒としては、便利な省略表現と文字通りの真実を区別したいですね。 もし、円が本当に無限に多くの辺を持つ多角形であることに固執するなら、その辺は何なのか、という問題が出てきます。 という疑問が湧く。もっともらしい答えは、円を構成する個々の点である。 この辺の長さはどのくらいだろうか。 0センチメートルです。 これらの辺は、角で区切られているのでしょうか？ どうやら、角が全くないか、すべての点が辺であり角でもあります。

長さゼロの辺は…問題のある概念と言えると思います。 どうやったら、あるのかわかるのでしょうか？ たとえば、私がこのような八角形の極限として正方形が生じる系を研究しているとします:

この状況では、正方形には 8 つの辺があり、そのうち 4 つは長さが 0 であると考えることは十分に意味があるかもしれません。 しかし、私の (完全に普通の) 正方形が本当に 8 つの辺を持っていると主張したら、あなたは眉をひそめるかもしれません。

ですから、私の投票で優勝したこの答えは、私が決定的に間違っていると宣言する唯一のものであり、また幾何学的洞察をまったく提供しない唯一のものでもあるのです。 パラドックス？ そうではありません。 類推によって推論することは、数学においても人生においても貴重なスキルです。同時に、それが私たちが行っていることだという認識を持ち続けることが重要です。

For infinitely many sides: geometrically illuminating.
Against infinitely many sides: 8-sided squares.

Off on a tangent 1: apeirogons

円はそうでなくても、無限に多くの側面を持つ多角形というのはあるのだろうか。 さて、そのようなものを表現する言葉として、アペイロゴンがあります。 正方形のアペイロゴンは、等しい（0でない）長さの辺とその間の角が等しいということになります。 ここでの唯一の選択肢は、この呆れるほど刺激的でないオブジェクトです：

これが「多角形」であることに反対なら（180°の角度やループで閉じない辺のチェーンのため）、次のようなものはどうでしょう。 円の底からスタートし、各段階で円の残りの半分を移動し、移動した円弧を直線に置き換える：

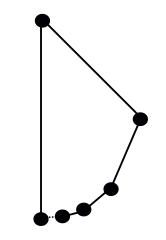
これは本物の多角形でしょうか。 これも用語によります。 一般的な定義である「閉じた多角形の鎖」によれば、開始角（左下）は1つの辺にしか接続しないので、これは適格ではありません。 しかし、その点は右からの一連の辺の限界であり、この形状は「非自己交差区分線形閉曲線」（人々が使う多角形の別の定義）になっているので、非常にニアミスです。 アペイロゴン（正アペイロゴンも）は単純に存在します。

Off on a tangent 2: extreme points

円は無限に多くの辺より無限に多くの角を持つと言った方が守備範囲が広いかもしれません（これはあまり聞かれる質問ではないようですが）。 そもそも、正方形の角がその境界線が直線でない点だとすると、円上のすべての点がそれを満たしていることになります。 さらに高度なことを言えば、図形の極点という概念がある。それは、その点でのみ図形に接する直線の線分を引くことができる任意の点のことである。 正方形や多くのよく知られた図形では、極点は角と正確に一致する。

このシェブロンのように、極点でない角を持つ図形があることを心配するかもしれません：

ここでは中央下の角は極点ではありません（他の3つの角は極点です）。 何が問題かというと、この形が凸でない（大雑把に言うと、出っ張りがありすぎる）ことです。 円は凸なので、心配はいらないかもしれません。 あるいは、問題の図形とその補体、つまり図形を切り出した平面全体の極点である点を「角」と定義することで、この状況を改善できるかもしれない。 この方法では、シェブロンを含むすべてのポリゴンの角を検出することができる。

片側？

小学校では、「片側」という答えにチェックが入るようです。 そして、中々まともな正当性があるのです。 上の定義1を思い出してください：

1.

平面図形の境界の一部を形成する線。

特に直線性にこだわらない場合、何が「線」としてカウントされるかが当面の問題です。 もしこの点についてあまりに寛容であれば、どんな平面図形でも、境界、周囲、円周と同じ意味で「一辺」を持っていると言えるでしょう。 しかし、これは間違いである。正方形は4つであるべきなのだ。 正方形は、4つの滑らかでない点と、その間にある4つの滑らかな部分を持っている。 もしかしたら、私たちがずっと数えていたのは、本当は滑らかな部分のことだったのかもしれない。 そこで、暗黙のうちに定義1を新しく改良しました（また、この機会に曖昧な用語「図形」を捨てました）：

4. piecewise-smooth closed curveの各平滑部。 「Piecewise-smooth “とは、滑らかな部分から作られ、孤立した非滑らかな点で合流することを意味します。 このような形状の境界の滑らかな部分を数えたいと思うのは完全に正当なことであり、その際に「辺」という言葉を使うのは決して無茶なことではありません。

問題は、「側面」のその解釈が単に首尾一貫しているだけでなく、明示的に記述されなくても単に推定できるほど自然であるかどうかです（めったにそうではありませんけど）。 滑らかさとまっすぐさが違うとどうなる？ 正方形の上部を同じ直径の半円に置き換えた、この墓石の形を考えてみましょう。

これは 2 つの滑らかな部分（下線と残りの部分）を持っていますが、3 つの直線状の辺（さらにそのうちの 2 つを滑らかにつなぐ曲線状の部分）があります。 では、何面あるのでしょうか。 またTwitterの友達に相談しました：

今回は「無限に多い」を選択肢に入れるべきでしたが、これは「特になし」に吸収されますね。 円は無限に多くの側面を持つと投票した人は、この形状の性質が読者に異なる「側面」の概念を示していない限り、ここでは自動的に「該当なし」に投票するはずです – 重要な注意点ですが -。

2 は上記の定義 4 と円の一辺性との互換性があり、完全に立派な答えですが、私はそれが決定的に正しいとは思っていませんし、3 や 4 が決定的に間違っているとも思っていません。 それは、何を数えるかによる。滑らかな部分、まっすぐな辺、まっすぐな辺とその後に残るもの、文脈によってはどれでも欲しい答えになるかもしれない（これについては後で詳しく述べる）。 また、平滑部の数を数えることが、私の「辺」という言葉の直感と完全に一致するかどうか、確信が持てない。 というのも、この墓石の2つの直立部分は、「反対側」にあると言ってよいからです。

私が「側面」の2つの異なる意味を混同している、用語は時に衝突するものであり、我々はそれに耐えなければならない、と抗議されるかもしれません。 しかし、私はそうではありません。 この演習のポイントは、2つの概念がかなりうまく噛み合っている状況（直方体）から外挿することなのです。 もし、私たちが気に入っているものをすべて取り入れた上で、より広い範囲の図形に適用できる新しいアイデアがあれば、それが唯一無二の正解であると主張できるはずです。 しかし、一般化の試みが、元の形状の望ましい側面を犠牲にするものであるならば、唯一正しい一般化というものは存在しないのかもしれません。

ここに別のバリエーションがあります。正方形の上辺を、どこにも滑らかでない無限にくねくねした線であるワイエストレス関数の一部で置き換えることによって作成したワイエストラス墓標です。

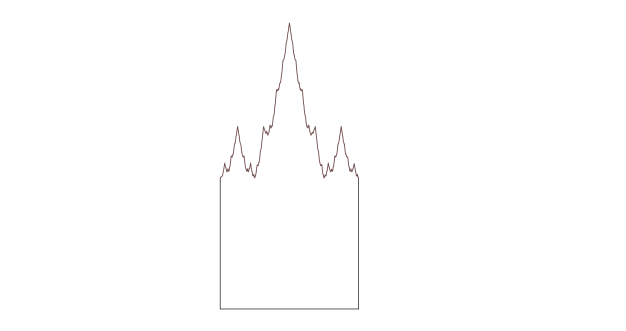
以下は、私の Twitter の友人たちがこれに対して立てた意見です (タイプミスを見つけてください)。 一方、滑らかな面を好むのであれば、無限に多くの面（そのうち3つは長さ1、残りは長さ0）を持っていると見るか、3つの面と間違いなく面でない境界を持つかの選択を迫られるわけです。

一辺：滑らかな一本の曲線
一辺に対して：反対側の同じ辺

余談3：辺と縁

正方形の辺は何本あるのでしょうか。 4つです。 辺はいくつありますか。 4つです。 では、辺と縁は同じものなのでしょうか？ そうとは限りません。 ここに、少なくとも間違いなく 4 辺でありながら、それぞれ 5 個と 3 個の辺を持つ 2 つの構成があります：

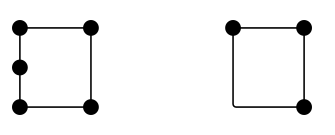
通常、「辺」は位相的オブジェクトであり、その形状ではなく機能が重要であると私は言っています。 ロンドンの地下鉄の地図を思い浮かべてください。 あのネットワークにいくつエッジがあるかというと、まっすぐな部分や滑らかな部分を集計しても意味がないんです。 すでに述べたように、多角形を閉じた多角形チェーンと呼ばれる非常に単純なネットワークとして考えるのが一般的です。 このとき、辺と辺は一致し、頂点と角も一致する。 しかし一般に、上記の 2 つの小さなネットワークのように、この一致を破ることができます。

ネットワーク理論的に物事を考えたいのに、頂点が明確にマークされていない場合、それらがどこにあるかを推測する必要があります。 多角形の場合、これは簡単です。頂点は角にありますから、幾何学的アプローチと位相的アプローチを自然に切り替えることができるわけです。 しかし、上の墓石のように、他の形状の場合は、それほど明白ではないかもしれません。 しかし、いずれの場合も、どこかに頂点があると言われて、その場所を尋ねられたら、4つ、つまり元の正方形の角であり、何らかの理由で上辺が直線でないものとして表現されていると推測するのは賢明だと思います。 そして、もしそのように考えるなら、墓石にはそれぞれ4つの辺があることになり、（論理的には首尾一貫しているのですが！）奇妙に思えるかもしれません。特に上辺は、その形状にもかかわらず、明らかに「片側」であるため、）他の数の辺を持っていると主張する。 実際、推測するのではなく、私の Twitter の返信者の 1 人が私に「両方の頂点が削除されたのですか」と尋ねました。 問題は、円上のどの点も他の点よりも頂点であることを主張できないことである。 したがって、円を1つの辺を持つネットワークとして見ることは魅力的ですが（そしてまた首尾一貫して）、もし我々が頂点を挿入しようとするなら、他のどの数よりも1を好む明白な理由はありません。

我々はそれを頂点のないネットワーク、駅のない地下鉄線のようなものとして見ることができますか？ ネットワークの通常の数学的概念はそれを許さないでしょうが、それは私たちをあまり躊躇させないはずです。 これは、純粋にトポロジカルなアプローチを示唆している。 しかし、この考え方では、円は頂点も辺もない一種のネットワークかもしれないが、（地下鉄の線路がたまたまそうなっているのであれば）正方形もそうである、という問題点がある。 トポロジーでは、正方形は円である。 (これはパラドックスではなく、境界が1つのループであり、その形は重要ではないと言っているに過ぎない）。 つまり、この種のネットワークは「1つの辺」を持っていますが、明らかに正方形は「1つの辺」を持っていないので、上の写真の2つの小さなネットワークと同じように、辺（幾何学的）と縁（位相的）の関係が再び崩れてしまっているのです。

辺がないか

円（あるいはどんな形でも）には「辺がない」と主張するのは、逆説的に思えるかもしれません。 しかし、その弁護の論拠は簡単です。 定義2に戻ります：

2. 平面図形の境界の一部をなす直線。

これは正方形の辺を完全にとらえた、シンプルでわかりやすいフレーズです。 これを曲がった図形に満足に一般化できるものが見つからなかったので、オリジナルにこだわるのが一番です。

For no sides: 「辺」の賢明な概念によれば正しい。
Against no sides: 禅の公案のように聞こえる。

None of the Above?

Googleが提供する定義を思い出してください：

3 平面直線の図形の境界を形成する各線。

これを円（非直線図形）に適用しようとすると、何も生じません。 この質問は「月曜日の辺はいくつあるか」と同じくらい無意味です。

定義3は最も正式なものなので（この投稿で唯一、私や私の子供たちが作ったものではない）、「上記のどれでもない」が断固として正しい答えになるのではないでしょうか? そうかもしれませんね。 一方、誰かが私たちに質問を投げかけたとき、慈善の原則はおそらく、私たちがしっかりとそうでないことを証明できない限り、それが意味のあるものだと仮定することを要求し、定義1、2、4やその他の変種がそれを可能にする。

上記のどれにも当てはまらない場合：意味的誤作動
上記のどれにも当てはまらない場合：対話的慈善

正しい答え

なぜこの記事を書くことになったのか？ 無数の小学生と同じように、冒頭の小学生である私の5歳の双子の息子も、最近、宿題でこの質問をされました。 一人は「1」、もう一人は「0」を選んだのですが、その理由を上記のように捉え、展開してみました。 どちらの答えも完全に正しいと思います。

では、質問をされたらどうすればいいのでしょうか。 円は何辺あるのか？ 私の意見では、最適な対応は、身近な数学者にこのトピックについて 3000 語の論文を書いてもらうことです。 しかし、そうでない場合は、ソクラテスの例に倣って、質問に対して反問で答えるのが最良の方法である。

結局のところ、0まで数えたり、1まで数えたり、質問に答えるのを拒否したりしても、円の幾何学については何もわかりません。 しかし、慣れ親しんだ概念を切り離し、余分な条件を削除したり追加したり、ある文脈からわずかに異なる文脈に移動して私たちの直感に挑戦したり、特定の設定で特定の用語が意味することを正確に書き留めようとすることによって得られるものはたくさんあります。 それが本当の数学なのです。

脚注

他の方法もあります。例えば、円周上の出発点Pを決めて、そこから円周上の距離を測定するのです。 そして、P から合理的な距離の点を角、それ以外を辺と宣言します。 これは、数え切れないほどの無限個の角と、数え切れないほどの無限個の辺をもたらす効果がある。 あるいは、その逆を規定することもできる。 これは円に対する多角形極限アプローチには好都合かもしれませんが、「正解」とみなされるほど簡単で明白であることには同意しかねます。

Twitterの反応者の一人が、曲線がどれだけ滑らかかを気にしておられました。 この墓石は連続微分可能ですが、2回微分可能ではありません。 多くの人がこれを致命的な問題と考えたら確かに面白いでしょうし、これはおそらくこのようなものから作られた無限に滑らかな墓石でテストできるでしょうが、私は詳細を考えていません。

これを次のように公式化してみるかもしれません：正方形（または任意のポリゴン）において、一辺は、内部の任意の位置から開始して、選んだ面が切り口の一面にしっかりとあるように、位置をまっすぐに通して形状を切断できる性質を持っています。 しかし、2面体の墓石はそうはいきません。 これを弱めるために、側面として数えるには、少なくとも、その側面が切り口の片側に来るように図形を切り開く方法がなければならない、と言うことができます。 そうすると、墓石には4つの側面があると言えるようになります（ただし、上部の領域では、曲がった部分が点の一辺にない）。 しかし、円の場合、その想定される一辺は決して一辺ではなく（だから除外される）、半円の直線部分だけが一辺とカウントされることになります。

両方の墓石に有効な厳密な正当化を思いつくのは簡単ではありませんが、私はより非公式にシェリングポイントの観点で考えています：つまり、事前に予測するのが簡単ではない理由で特別であることが目立つ場所です。