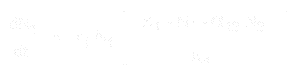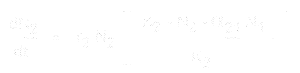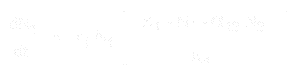| 種間競争 |
種間の不利益は両方向に流れるかもしれないし、優れた競争者はほとんど影響を受けないかもしれない。 |
|
同じ種のメンバー間の競争よりも一般的に激しくない。
+ は正の効果を意味し、負の効果を意味する。
しかし、同一のニッチを占める2つの種の理論的なケースを考えてみよう。 Gause (1934) は、同じ細菌細胞を餌とする 2 つの原生生物種を研究した。 この2種を1つの培養器に入れると、一方は常に他方を絶滅に追いやったのです。 その後、多くの実験により、「ガウスの法則」(現在は「競争的排除の原理」と呼ばれている)は支持されている。 これは、同一の資源を利用する2つの種は無限に共存できない、あるいは「完全な競争相手は共存できない」(Hardin 1960)というものである。
多くの実験により、生息地内の2つの種の資源利用が異なれば異なるほど、実際に共存できる可能性が高くなることが実証されている(Krebs 1994)。 重複する部分が多い2つの種であっても、競争的相互作用によって一方または両方の成長速度が抑制されることが多いが、しばらくの間は共存できるかもしれない。 時間の経過とともに、資源分割と呼ばれる興味深い現象が起こることがある。 それぞれの種のメンバーが、似たような資源のあるカテゴリーを細分化して専門化するようになるかもしれない。 例えば、両者がリンゴを食べる場合、一方は小さな青い実を食べ、もう一方はより大きく熟した実を食べるようになるかもしれない。
ロトカ=ウォルテラ・モデルは、2つの種が同じ資源をめぐって競争しているときに起こりうる結果を生態学者が予測できるようにするために開発された。 基本的に、このモデルは、ある種の存在が他の種の人口増加に与える影響を、同じ種の2つのメンバーがお互いに与える競争的影響と比較して説明しようとするものである。
種1の人口増加の方程式は:
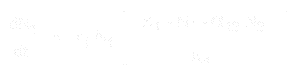
そして種2については:
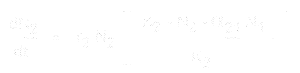
ここにある。
* N1とN2は種1と2の人口サイズ、
* r1とr2はこれらの種の固有増加率、
* K1とK2はそれぞれの種の生息地の収容力、
* α12とα21は一方の種が他方の種の人口増加に対する効果である。 具体的には、α12は種2の種1の成長に対する効果、α21は種1の種2の成長に対する効果である。
各式の値がわかっていれば(あるいは実験結果から経験的に推定できる)、その式を使って競合の潜在的結果(すなわち、共存できるのか、それともいずれ一方が他方を排除するか)を予測することが可能である。 K1、K2、a12、a21の値を用いて、両種のゼロ成長の等値線(すなわち、dN1/dtまたはdN2/dtがゼロになるところ)を同じグラフ上にプロットし、結果として得られる人口成長のベクトルの総和(トラジェクトリー)を用いて競争の結果を決定する(Figure 1). 種1と種2が共存し(左)、種1が種2を競争的に排除する(右)ゼロ成長の等値線グラフの例。
ロトカ=ウォルテラ競争モデルは、生態学的時間における2つの種の競争の結果を記述するものである。 ある種が別の種を競争的に排除できるため(図1)、競争的に劣位にある種は生き残るために食べる餌の種類を増やす可能性がある。 しかし、進化的時間における種間競争に対する種の反応は、生態的時間において起こるのとは逆のことが多い。 競争相手は一般に、特定の資源タイプに特化するようになる。 進化の過程で起こるこの資源分割は、実際には2つの種間の競争を減少させるか、あるいはなくす結果となる。
互いに特に近縁というわけではないが、2種の寄生蜂であるMelittobia digitataとNasonia vitripennisの生活史は非常によく似ている。 両種は同じ宿主を利用することができるが、自然界ではそれぞれ異なる宿主を利用していた。 MelittobiaはNasoniaの約半分の大きさだが、どちらもかなり小型で人間には全く無害である。
両者の完全なライフサイクルは比較的短く(25℃で2~4週間)、またよく似ている(図2)。 メスは宿主の体表に多数の卵を産み付ける。 卵は孵化して幼虫になり、宿主を食べ、蛹になり、最後に成虫に変態する。 Melitobbia digitataでは、雌成虫の翅は正常なものと発育不全のものがある。 正常な翅を持つ成虫は、宿主から分散して新たな餌資源を探す。 飛べない雌は出てきた宿主に産卵するか,同じ巣の中で新しい宿主に分散する(Freeman and Ittyeipe 1976, Côsoli and Vinson 2002)
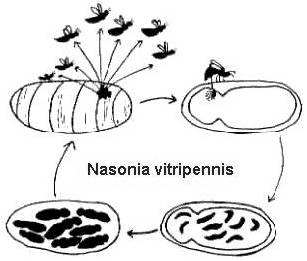
Figure 2. Neobellieria bullataを宿主とするNasonia vitripennisの蛹のライフサイクル(drawing by Bethia King)。 Melittobia digitataのライフサイクルも同様であるが、どのステージの個体も小さくなっている。
寄生虫の種類は世界で約7万種(全昆虫の9%)知られているが、その数は80万種にも及ぶと推定されている(Strand 2002)。 そのうちの約8割は、この研究室で使う2種と同じく、ヒメバチ目に属する。 自然界では、宿主は複数種の寄生虫に寄生されることがあり、すべての寄生虫が同じ資源をめぐって競争しています(Stand 2002)。 宿主種自身が他の種に寄生している場合もあるので、その競合が群集構造に与える生態学的影響は非常に複雑なものになります。 たとえば、北米の大規模なジャックパイン林を攻撃し、落葉させ、枯らすことがあるスウェインジャックパインソーバエ (Neodiprion swainei Midd.) は、11種の寄生バチを宿主とする。 これらの種の多くは、宿主のライフサイクルの異なる段階、あるいは宿主集団の異なるセグメントに寄生することで、宿主資源を分割して共存しているようである (Price 1972)。 ノコギリの繭を攻撃する寄生虫ギルドの一員に、外来種(Pleolophus basizonus)がいる。 この種は優れた競争者であり、その存在がいくつかの競争者種の豊度を決定している (Price 1970)。 競争は寄生虫の群集構造に影響を与えるが、寄生虫間の種間競争がある場合でも、宿主資源の空間的・時間的変動が寄生虫種の豊かさを決定する上でさらに重要であると考えられる (Hawkins 2000)。
農作物や森林樹木の重要な害虫を宿主とする寄生虫は、害虫個体群の生物的防除として意図的に放たれることがあります。 複数種の寄生虫が同じ宿主を攻撃する場合、放流を行う前にその競争の性質を理解することが重要である。 異なる寄生虫種が資源分配によって共存できる場合、一部または全部の寄生虫種を導入することで有害生物宿主の防除が最もうまくいく場合があります。 一方、競争相手が競争的相互作用によって互いの個体数を制限している場合、寄生虫種のうち最も効率のよい種を単独で放つことで害虫の最大限の防除が可能になるかもしれない(Amarasekare 2000)。
<top>
Materials and Methods.に掲載されています。
データ収集と分析方法の概要。
ラボ1:
表1で議論されている相互作用のカテゴリは、単に読んでいるだけでは非常に単純に思えるかもしれない。 しかし、もしあなたが見慣れない2つの動物の相互作用を観察したら、どのように適用すべき「ラベル」を決定しますか? また、その相互作用の結果を予測することができるだろうか? その予測はどのように検証できますか?
この研究室の調査で紹介された2つの寄生蜂は、似たようなニッチを占めているようです。 この2種の間の相互作用に興味があります。 さらに、一方の種が他方の種に与える影響を定量化できるようにしたい。
各グループがすべきこと。
– 2つの寄生蜂、Melittobia digitataとNasonia vitripennis、および単一の宿主、Neobellierriaを含む設定可能なすべての実験の組み合わせについて議論し、リストアップしてください。
– 実験で操作する変数を特定しリストアップする、
– 実験で一定に保つ変数を特定しリストアップする、
– それぞれの種が他に及ぼす影響を定量化するために測定したい従属変数を特定しリストアップする。
各グループは、クラスの他のメンバーで実験計画を共有します。 クラスとして一緒に、コンセンサスとなる実験デザインを作成する。 コンセンサスとなった実験デザインに基づいて、各自が各処理について1つの複製培養をセットアップすること。 下記の「寄生虫の取り扱い」を参照。 クラス全員のデータをプールして解析する。
毎週の確認事項
毎週、各自が自分の培養物を検査して、スズメバチの成虫が出現しているかどうかを確認する。 各培養物について、最初に成虫の出現を確認した日を記録しておくこと。 ナゾニアの培養液は樹立から21日後に冷凍保存すること。 Melittobiaと混合種の培養物は、42日後に凍結する。
第2研究室(第1研究室から6週間後)。
各自、各複製培養で生じた子供の数を数えること。 クラスのデータをプールできるように、データをスプレッドシートに入力する。 プールしたデータを使って、ロトカ=ボルテラの競争モデルのパラメータを推定し、競争の効果の統計分析に利用する。
グループ内で、データをどのように使ってLotka-Volterra競争モデルのパラメータを定量化できるか議論する(以下の「Lokta-Volterra競争モデルの定量化」参照)。 また、この2種の寄生虫における種内競争と種間競争の相対的重要性について、特定の処理の比較から何がわかるかを議論する(以下の「データ解析のガイドライン」を参照)。
寄生虫を扱う。
両寄生虫、Melittobia digitataとNasonia vitripennisの成虫は、非常に “使いやすい “です。 メスは普通の翅を持ち、飛ぶことができますが、なかなか飛びません。 しかし、彼らは負の地軸性(すなわち、重力に逆らって上方に移動する)を持っている。 培養した雌を数匹、水平面に振り出し、逆さにしたガラス瓶を被せると、容易に瓶の中に入り、側面をよじ登ることができる。 バイアルにスズメバチを入れたら、宿主のサナギを入れ、バイアルを綿でしっかりと塞ぐと簡単である。 このようにして、大量の個体を効率よく処理することができます。 また、成虫になったスズメバチは、短いパイプクリーナーで一時的に付着させ、操作することもできます。
ロトカ=ボルテラ競争モデルの定量化
ロトカ=ボルテラ競争モデルは「はじめに」で説明し、方程式で定義した。 そこで述べたように、もし各式に対する値が実験結果から経験的に推定できるならば、その式は競争の潜在的な結果(すなわち、2つの種が共存するか、あるいは一方が最終的に他方を排除するか)を予測するために使用することが可能である。 K1、K2、α12、α21の値を用いて、両種のゼロ成長の等値線(すなわち、dN1/dtまたはdN2/dtがゼロになるところ)を同じグラフ上にプロットし、結果として得られる人口成長のベクトルの総和(トラジェクトリー)を用いて、競争の結果を決定することができる。
実験計画に基づいて、これらのパラメーターの値を決定する必要がある。 ある集団の環境収容力がその生息地で生存できる最大個体数であることを想起してほしい。 この実験では簡単のために、寄生虫の生息地を1つの宿主と定義した。 もちろん、実際には、1つの生息地には複数のムシロチョウの巣やクロバエの蛹室があり、潜在的に利用可能な宿主が多数存在すると思われる。 この2つの種の環境収容力を求めるには、ある種のみが存在するときに、1つの宿主から生み出されるある種の子孫の最大数を知ることが必要である。 このことを念頭に置いて、MelittobiaとNasoniaの環境収容力を推定するには、どちらの処理から得られたデータを使用しますか? (環境収容力ではすべての宿主資源が使用されることを忘れないでください)
競争係数(α12、α21)を推定するのはもう少し複雑です。 種1の人口増加の方程式が次の通りであることを思い出してください:
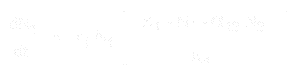
寄生虫によってすべての宿主資源が使われると、もはや人口は増加しないでしょう。 つまり、dN1 /dt = 0となり、K1 – N1 – alpha12*N2 = 0のときにこの状態になります。 上で、収容力の求め方を説明した。 メリトビアが「種1」であると仮定して、その環境収容力を K1 に用います。 種間競争によって生まれるメリトビアとナゾニアの子供の数は、それぞれN1とN2である。 これを踏まえて、N1、N2を推定するには、どの処理のデータを使うか。
α12を計算したのと同じ方法で、α21を計算することができます。
さて、すべてのパラメータ値を計算したので、これらの値を使ってゼロ成長の等値線をプロットし、MelittobiaとNasoniaの間の競争の結果を予測することができます。
データ解析のガイドライン
異なる処理間の比較を使用して、種内競争と種間競争の相対的な重要性を探ることができる。 まず、それぞれの処理でどのような種類の競争、種内競争または種間競争が起きているかを確認する(もしあれば)。 これを行った後、処置の組の間のすべての比較について考えてみてください。 それぞれの比較から何がわかりますか? 比較とその意味を一覧にした表を作成すると便利かもしれません。 すべての比較は2つの治療を含んでいるので、t検定を使って統計的に分析することができます。
<top>
Questions for Further Thought and Discussion:
- ロトカ=ウォルテラ競争モデルについて計算したパラメーター値に基づいて、2つの種の間の競争の予測結果はどのようになりますか。 予測された結果は、種間競争のすべての複製で達成されましたか。 そうでない場合、なぜそうでないのか。
- 「ガウスの法則」は、全く同じ資源を同じように共有する競争相手は共存できないことを述べている。 これは、競合する資源を最も効率的に利用する種が、最終的にその場所で他を排除することを意味します。 メリトビアとナゾニアの相互作用に、ガウスの法則は適用できそうですか?
- もしこの2つの種が自然界で同じ宿主を使うとしたら、資源分割によってどのように共存できるでしょうか。
- あなたの実験の結果に基づいて、なぜ2つの種は自然界で同じ宿主を使わないのでしょうか。
- 環境容量と競争係数の推定値が与えられたら、ポプラのロトカ=ボルテラ競争モデル(参考文献とリンク参照)を使って、メリトビアとナゾニアの競争の結果を予測しなさい。 予測された競争の結果は、初期人口サイズや人口成長率に影響されますか? もしそうなら、どのように? 均衡に達するまでの時間はこれらの値によってどのように影響されますか。
- 環境収容力と競争係数は単なる推定値に過ぎません。
- もしこれらの種で種間競争が起こっているなら、どのようなメカニズムで競争(干渉か搾取か)が起こっているのか、どのように判断したらよいでしょうか。
*** 注:これらの質問の多くに対する回答や寄稿者による他の多数のコメントは「教員への注意事項」に掲載されています。 Comments On Questions for Further Thought “のページでご覧いただけます。
<top>
参考文献とリンク:
<top>
Tools for Assessment of Student Learning Outcomes.Odienst は、学生の学業成果の評価ツールです。
評価は、この演習を利用したさまざまな機関で、さまざまな方法で実施されてきた。 すべての場合において、学生は、各学生が個人的に、またはグループの学生が書いた科学論文に基づいて評価される。 場合によっては、論文の第一稿と第二稿の両方について評価されることもある。
論文の採点基準は講師によって異なります。 以下は、モーハウス・カレッジで使用されている採点基準の例で、科学論文の構成要素のうち方法を除いた「結果の要約」に対するものである。 この評価基準では、「読者」は、学生による適切な読者の選択に関わるものです。 学生は、レポートを科学論文であるかのように書くことが期待されています。 したがって、適切な読者は、実験を行ったことはないが、科学的な知識を持つ仲間である。 講師やクラスの他の学生に向けて書かれたレポートには、適切な読者がいません。 “フォーマット “とは、並列的な構成を持ち、互いに構築し合うセクションにおけるレポートの全体的な構成のことです。 例えば、「考察」では、「結果」で報告された結果を評価し、その結果をより大きな文脈に当てはめる必要があります。 また、「Discussion」では、「Introduction」で述べた仮説に言及する必要があります。
| Results Summary Evaluation (50 points possible) |
| Introduction and Title Page (10 points) |
_____ |
| Results (10) ポイント) |
_____ |
| Discussion and Conclusions (10 points) |
_____ |
| Literature Use and Citations (10 points) |
_____ |
| Format.Discussion and Conclusions (10 points) |
[7] Discussion and Conclusions (10 points) Audience (10 points)
_____ |
|
入門レベルでは、クラスで作成したすべての表、ディスカッションクエスチョンの返答、調査の進行に関するノートを週ごとに提出します。 個人の科学論文に加えて、グループ科学論文、グループ口頭発表、グループポスター発表の形で実験結果を発表することも可能です。 しかし、生徒全員が同じ実験を行い、同じ結果を発表するのですから、個人またはグループの科学論文が最も効果的でしょう。
<top>
この実験の形成的評価のためのツール。
モーハウスカレッジの生態学のコースでは、各学生は、生態学の講義コースで取り上げられた主題の知識と理解を強化する上で、各研究室の演習がどのような効果を持つか、10点満点で評価するよう求められている。 さらに、どの演習が最も楽しくなかったか、また、どの演習が最も科学的方法の理解を深めたかについても質問している。 この情報は、次の学期で使用する演習の選択と修正に使用される。
エモリー大学とラドフォード大学の生態学のコースでは、各学生にどの演習が一番好きで、どの演習が一番嫌いか質問される。 学生は、なぜそのように演習を評価したのかについて、コメントを寄せることもあります。 この情報もまた、次の学期で使用する演習を修正するために使用されます。
評価に関する広範な考察は、このサイトの教授法のセクションにあります。
|