モデルの予測について議論するとき、必ず予測誤差(バイアスと分散)を理解することが重要です。 モデルのバイアスおよび分散を最小化する能力の間にはトレードオフがあります。 これらの誤差を正しく理解することは、正確なモデルを構築するだけでなく、オーバーフィッティングやアンダーフィッティングの失敗を避けるためにも役立ちます。
では、基本から始めて、それらが機械学習モデルにどのような違いをもたらすかを見ていきましょう。 バイアスの高いモデルは、学習データにほとんど注意を払わず、モデルを単純化しすぎています。 分散とは、与えられたデータポイントに対するモデル予測のばらつき、またはデータの広がりを示す値です。 分散が大きいモデルは、学習データに多くの注意を払い、見たことのないデータには汎化しません。 その結果、このようなモデルは学習データでは非常によく機能しますが、テストデータでは高いエラー率になります。
Mathematically
我々が予測しようとしている変数をY、その他の共変数をXとします。 両者の間には
Y=f(X) + e
ここでeは誤差項で、平均0と正規分布している
線形回帰や他のモデリング手法を用いてf(X)のモデルf^(X)を作成することにする。
そこで、ある点xにおける期待自乗誤差は
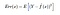
となる。 Err(x)はさらに

Err(x) は Bias² の和と分解される。 分散と既約誤差があります。
再現可能誤差とは、良いモデルを作っても減らすことができない誤差のことです。 これは、データ中のノイズの量を示す指標です。 ここで重要なのは、どんなに良いモデルを作っても、データには除去できないノイズや再現不可能な誤差があるということです。
Bias and variance using bulls-eye diagram

上の図で、目標の中心は正しい数値を完全に予測するモデルであるとします。 的から遠ざかるにつれて、予測値はどんどん悪くなっていく。 教師あり学習では、モデルがデータの基本的なパターンを捉えることができない場合、アンダーフィットが起こります。 このようなモデルは通常、高いバイアスと低い分散を持っています。 これは、正確なモデルを構築するためのデータ量が非常に少ない場合や、非線形データで線形モデルを構築しようとした場合に起こります。 また、この種のモデルは、線形回帰やロジスティック回帰のように、データの複雑なパターンを捉えるには非常に単純である。 これは、ノイズの多いデータセットに対してモデルを大量に訓練した場合に起こります。 このようなモデルはバイアスが低く、分散が大きい。 これらのモデルは、決定木のように非常に複雑で、オーバーフィットになりがちです。

Bias Variance Tradeoff?
<8758>モデルが単純すぎてパラメータ数が非常に少ない場合、高バイアスおよび低バランスとなるかもしれない。 一方、モデルが多数のパラメータを持つ場合、高い分散と低いバイアスを持つことになります。
このような複雑さのトレードオフが、バイアスと分散の間にトレードオフがある理由です。 アルゴリズムは、より複雑になると同時に、より少なくすることはできません。
Total Error
良いモデルを構築するには、合計誤差を最小化するようなバイアスと分散の良いバランスを見つける必要があります。


偏りと分散の最適バランスが、モデルをオーバーフィットしたりアンダーフィットすることはないだろう。
したがって、バイアスと分散を理解することは、予測モデルの挙動を理解するために重要です。
お読みいただきありがとうございました!
。