Prerequisito – Teoria Gráfica Básica – Conjunto 1
Um gráfico é uma estrutura que corresponde a um conjunto de objetos em que alguns pares dos objetos estão de alguma forma “relacionados”. Os objetos do gráfico correspondem a vértices e as relações entre eles correspondem a arestas. Um gráfico é representado esquematicamente como um conjunto de pontos representando vértices conectados por linhas ou curvas representando arestas.
Formalmente,
“Um gráfico 
consiste em 
, um conjunto não vazio de vértices (ou nós) e 
, um conjunto de arestas. Cada aresta tem um ou dois vértices associados a ela, chamados seus pontos finais”
Tipos de gráfico :Existem vários tipos de gráficos distinguidos com base nas arestas, sua direção, seu peso etc.
1. Gráfico simples – Um gráfico no qual cada aresta conecta dois vértices diferentes e onde não há duas arestas conectando o mesmo par de vértices é chamado de gráfico simples. Por exemplo, considere o seguinte gráfico –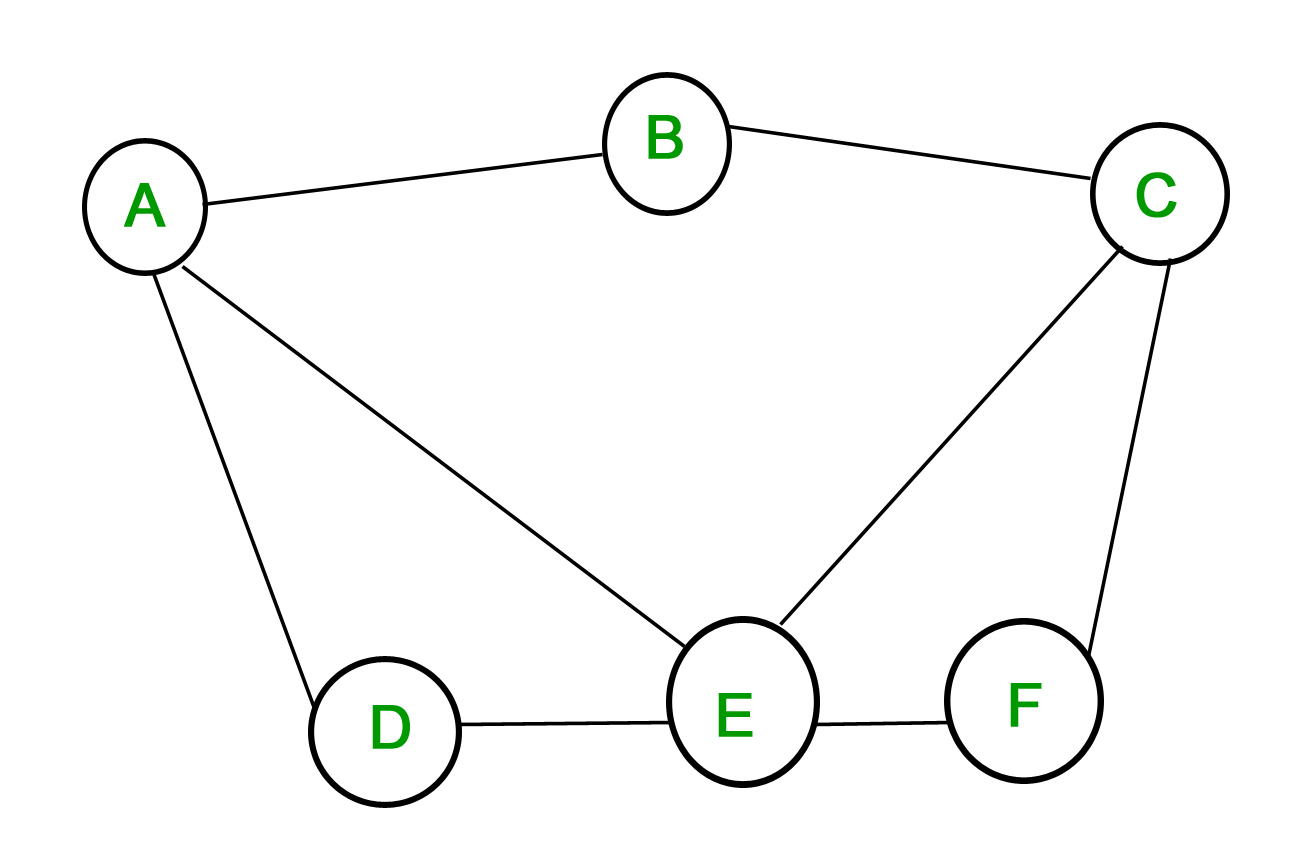
O gráfico acima é um gráfico simples, uma vez que nenhum vértice tem um auto-laço e nenhum dois vértices têm mais de uma aresta conectando-os.
As arestas são denotadas pelos vértices que elas conectam- 
é a aresta conectando os vértices 
e 
.
2. Multigraph – Um gráfico no qual múltiplas arestas podem conectar o mesmo par de vértices é chamado de multigraph.
Desde que pode haver múltiplas arestas entre o mesmo par de vértices, a multiplicidade de arestas informa o número de arestas entre dois vértices.
O gráfico acima é um multigraph já que há múltiplas arestas entre e 
. A multiplicidade da aresta 
é 2,
Em alguns gráficos, ao contrário do mostrado acima, as arestas são direcionadas. Isto significa que a relação entre os objetos é unidirecional e não bidirecional. A direção das bordas pode ser importante em algumas aplicações.
Baseado em se as arestas são direcionadas ou não, podemos ter gráficos direcionados e gráficos não direcionados. Esta propriedade pode ser estendida a gráficos simples e multigráficos para obter gráficos simples direcionados ou não direcionados e multigráficos direcionados ou não direcionados.
Basic graph Terminologia do gráfico :
Na discussão acima alguns termos referentes a gráficos já foram explicados, tais como vértices, bordas, bordas direcionadas e não direcionadas, etc. Há mais termos que descrevem propriedades de vértices e arestas.
- Adjacência – Em um gráfico
dois vértices 
e 
são ditos adjacentes se eles forem os pontos finais de uma aresta. A borda 
é dita como incidente com os vértices.
Caso a borda seja dirigida, é dita como adjacente a e é dita como adjacente a partir de . Aqui, é dito ser o vértice inticial e é dito ser adjacente ao vértice terminal. - Grau – O grau de um vértice é o número de arestas incidentes com ele, exceto o auto-loop que contribui duas vezes para o grau do vértice. O grau de um vértice é denotado como
.
No caso de gráficos dirigidos, o grau é ainda classificado como in-degree e out-degree. O in-degree de um vértice é o número de arestas com o vértice dado como vértice terminal. O out-degree de um vértice é o número de arestas com o vértice dado como o vértice inicial. In-degree é denotado como
e out-degree é denotado como 
.
Por exemplo, no gráfico acima, que mostra voos entre cidades, o in-degree do vértice “Delhi” é 3 e seu out-degree também é 3.
Note: Se um vértice tem grau zero, ele é chamado de isolado. Se o grau é um, então é chamado de pendente.
Theorem do handshaking :
What would one get if the degrees of all the vertices of a graph are added. No caso de um gráfico não direcionado, cada borda contribui duas vezes, uma para seu vértice inicial e a segunda para seu vértice terminal. Então a soma dos graus é igual ao dobro do número de arestas. Este facto é referido no Teorema do aperto de mão.
Let be an undirected graph with edges. ThenIn case G is a directed graph,
O teorema do aperto de mão, para gráficos não direccionados, tem um resultado interessante –
An undirected graph has an even number of vertices of odd degree.
Prova : Let 
e 
sejam os conjuntos de vértices de graus pares e ímpares, respectivamente.
Sabemos pelo teorema do aperto de mão que,
So,
A soma dos graus de vértices com graus pares é par. O LHS também é par, o que significa que a soma dos graus dos vértices com graus ímpares deve ser par.
Assim, o número de vértices com grau ímpar é par.
alguns gráficos simples especiais :
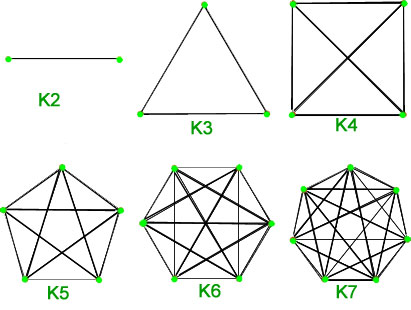
1. Gráficos Completos – Um gráfico simples de 
vértices com exatamente uma borda entre cada par de vértices é chamado de gráfico completo. Um gráfico completo de vértices é denotado por 
. O número total de arestas são n*(n-1)/2 com n vértices no gráfico completo.
2. Ciclos – Ciclos são gráficos simples com vértices 
e arestas 
. Ciclo com vértices é indicado como 
. O número total de arestas são n com n vértices no gráfico do ciclo.
3. Rodas – Uma roda é como um ciclo, com um vértice adicional que está ligado a cada outro vértice. Rodas de vértices com 1 vértice adicional são denotados por 
. O número total de arestas são 2*(n-1) com n vértices no gráfico do desdobramento.
4. Hypercubo – O Hypercubo ou n-cubo é um gráfico com 
vértices cada um representado por uma cadeia de n bits. Os vértices que diferem no máximo por 1 bit estão ligados por arestas. Um hipercubo de vértices é denotado por 
. O número total de arestas são n*
com vértices no gráfico de cubo.
5. Gráficos Bipartidos – Um gráfico simples é dito ser bipartido se seu conjunto de vértices pode ser dividido em dois conjuntos de disjuntos de modo que cada aresta em tenha seu vértice inicial no primeiro conjunto e o vértice terminal no segundo conjunto. O número total de arestas são (n*m) com vértices (n+m) no gráfico bipartido.
Theorem – Um gráfico simples é bipartido se e somente se for possível atribuir uma das duas
diferentes cores a cada vértice do gráfico para que não sejam atribuídas duas adjacentes a
mesma cor.
Um gráfico bipartido com 
e vértices em seus dois subconjuntos desajustados é dito completo se houver uma borda de cada vértice no primeiro conjunto para cada vértice no segundo conjunto, para um total de 
bordas. Um gráfico bipartido completo com vértices no primeiro conjunto e vértices no segundo conjunto é denotado como 
.
GATE CS Corner Questions
Practicating the following questions will help you test your knowledge. Todas as perguntas foram feitas na GATE em anos anteriores ou em Testes de simulação da GATE. É altamente recomendado que você os pratique.
1. GATE CS 2013, Pergunta 25
2. GATE CS 2014 Set-1, Pergunta 61
3. GATE CS 2006, Pergunta 71
4. GATE CS 2002, Pergunta 25
5. GATE CS 2004, pergunta 37
6. GATE CS 2014 Set-2, pergunta 13
Referências-
Gráficos – Wikipedia
Matemática discreta e suas aplicações, por Kenneth H Rosen
Este artigo é contribuído por Chirag Manwani. Se você gosta de GeeksforGeeks e gostaria de contribuir, você também pode escrever um artigo usando contribute.geeksforgeeks.org ou enviar seu artigo pelo correio para [email protected]. Veja o seu artigo que aparece na página principal do GeeksforGeeks e ajude outros Geeks.
.