Kun keskustelemme mallien ennustamisesta, on tärkeää ymmärtää ennustusvirheet (harha ja varianssi). Mallin kyvyn minimoida harhaa ja varianssia välillä on kompromissi. Näiden virheiden kunnollinen ymmärtäminen auttaisi meitä paitsi rakentamaan tarkkoja malleja myös välttämään yli- ja alimitoituksen virheet.
Aloitetaan siis perusasioista ja katsotaan, miten ne vaikuttavat koneoppimismalleihimme.
Mikä on harha?
Harha on mallimme keskimääräisen ennusteen ja oikean arvon, jota yritämme ennustaa, välinen ero. Malli, jolla on suuri bias, kiinnittää hyvin vähän huomiota harjoitusdataan ja yksinkertaistaa mallia liikaa. Se johtaa aina suureen virheeseen koulutus- ja testidatassa.
Mikä on varianssi?
Varianssi on mallin ennusteen vaihtelu tietylle datapisteelle tai arvolle, joka kertoo datamme hajonnasta. Malli, jolla on suuri varianssi, kiinnittää paljon huomiota harjoitusdataan eikä yleistä dataa, jota se ei ole nähnyt aiemmin. Tämän seurauksena tällaiset mallit suoriutuvat hyvin harjoitusdatasta, mutta niillä on korkea virhemäärä testidatassa.
Matemaattisesti
Määritellään muuttuja, jota yritämme ennustaa, Y:ksi ja muut kovariaatit X:ksi. Oletamme, että näiden kahden välillä on sellainen suhde, että
Y=f(X) + e
Jossa e on virhetermi ja se on normaalisti jakautunut keskiarvolla 0.
Tehdään f(X):stä malli f^(X) lineaarisella regressiolla tai muulla mallinnustekniikalla.
Siten odotettu neliövirhe pisteessä x on
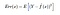
The Err(x) voidaan edelleen purkaa seuraavasti

Err(x) on Bias²:n summa, varianssi ja redusoimaton virhe.
Irreredusoituva virhe on virhe, jota ei voida pienentää luomalla hyviä malleja. Se on mitta datassamme olevan kohinan määrästä. Tässä on tärkeää ymmärtää, että riippumatta siitä, kuinka hyvän mallin teemme, datassamme on tietty määrä kohinaa tai redusoitumatonta virhettä, jota ei voida poistaa.
Virhe ja varianssi häränsilmä-diagrammin avulla

Yllä olevassa kaaviossa kohteen keskipisteen keskipisteenä on malli, joka ennustaa täydellisesti oikeita arvoja. Kun siirrymme kauemmas maalitaulusta, ennusteemme muuttuvat yhä huonommiksi. Voimme toistaa mallinrakennusprosessimme saadaksemme erillisiä osumia kohteeseen.
Valvotussa oppimisessa vajaasovitusta tapahtuu, kun malli ei pysty vangitsemaan datan taustalla olevaa mallia. Näillä malleilla on yleensä suuri harha ja pieni varianssi. Se tapahtuu, kun meillä on hyvin vähän dataa tarkan mallin rakentamiseen tai kun yritämme rakentaa lineaarisen mallin epälineaarisella datalla. Lisäksi tällaiset mallit ovat hyvin yksinkertaisia kuvaamaan datan monimutkaisia kuvioita, kuten lineaarinen ja logistinen regressio.
Valvotussa oppimisessa ylisovittamista tapahtuu, kun mallimme kuvaavat datan taustalla olevan kuvion ohella myös kohinaa. Se tapahtuu, kun harjoittelemme malliamme paljon meluisilla aineistoilla. Näillä malleilla on pieni harha ja suuri varianssi. Nämä mallit ovat hyvin monimutkaisia, kuten päätöspuut, jotka ovat alttiita ylisovittamiselle.

Miksi on olemassa harha-varianssin ja varianssin välinen kompromissi?
Jos mallimme on liian yksinkertainen ja siinä on vain vähän parametreja, sillä voi olla suuri harha ja pieni varianssi. Toisaalta jos mallissamme on suuri määrä parametreja, niin sillä on korkea varianssi ja matala harha. Meidän on siis löydettävä oikea/hyvä tasapaino sovittamatta dataa liikaa ja sovittamatta sitä liian vähän.
Tämän monimutkaisuuden kompromissin vuoksi on olemassa kompromissi harhan ja varianssin välillä. Algoritmi ei voi olla samaan aikaan monimutkaisempi ja vähemmän monimutkainen.
Kokonaisvirhe
Hyvän mallin rakentamiseksi meidän on löydettävä hyvä tasapaino harhan ja varianssin välille siten, että se minimoi kokonaisvirheen.
Siten harhan ja varianssin ymmärtäminen on kriittistä ennustemallien käyttäytymisen ymmärtämiseksi.
Kiitos lukemisesta!