Esittely
Informaatiotieteessä suunnattu asyklinen graafi (DAG, directed acyclic graph) on suunnattu graafi, jossa ei ole syklejä. Tässä opetusohjelmassa näytetään, miten DAG:lle tehdään topologinen lajittelu lineaarisessa ajassa.
Topologinen lajittelu
Monissa sovelluksissa käytämme suunnattuja asyklisiä graafeja osoittamaan tapahtumien välisiä etusijajärjestyksiä. Esimerkiksi aikataulutusongelmassa on joukko tehtäviä ja joukko rajoituksia, jotka määrittelevät näiden tehtävien järjestyksen. Voimme rakentaa DAG:n edustamaan tehtäviä. DAG:n suunnatut särmät edustavat tehtävien järjestystä.
Harkitaan ongelmaa, joka liittyy siihen, miten henkilö pukeutuu muodolliseen tilaisuuteen. Meidän on puettava päällemme useita vaatekappaleita, kuten sukat, housut, kengät jne. Jotkin vaatteet on puettava päälle ennen muita. Esimerkiksi sukat on puettava ennen kenkiä. Jotkin vaatteet voidaan pukea missä tahansa järjestyksessä, esimerkiksi sukat ja housut. Voimme käyttää DAG:ia havainnollistamaan tätä ongelmaa:
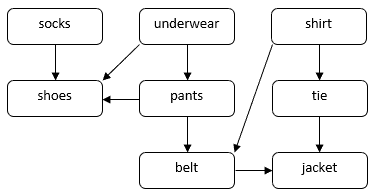
Tässä DAG:ssa kärkipisteet vastaavat vaatteita. Suora särmä 
DAG:ssa osoittaa, että meidän on puettava vaate 
päällemme ennen vaatetta 
. Tehtävämme on löytää järjestys kaikkien vaatteiden pukemiselle riippuvuusrajoituksia kunnioittaen. Voimme esimerkiksi pukea vaatteet seuraavassa järjestyksessä:
DAG:n 
topologinen lajittelu on sen kaikkien kärkipisteiden lineaarinen järjestys, joka on sellainen, että jos sisältää reunan , niin esiintyy järjestyksessä ennen . DAG:lle voidaan konstruoida topologinen lajittelu, jonka suoritusaika on lineaarinen kärkipisteiden ja särmien lukumäärään nähden, eli 
.
Kahnin algoritmi
DAG:ssa kaikilla kahden kärkipisteen välisillä poluilla on äärellinen pituus, koska graafi ei sisällä sykliä. Olkoon 
pisin polku (lähdepiste) ja (kohdepiste) välillä. Koska on pisin polku, ei voi olla yhtään saapuvaa reunaa :een. Näin ollen DAG sisältää vähintään yhden pisteen, jolla ei ole saapuvaa reunaa.
3.1. Kahnin algoritmi
Kahnin algoritmissa rakennetaan topologinen lajittelu DAG:lle etsimällä sellaisia kärkipisteitä, joilla ei ole saapuvia särmiä:
Tässä algoritmissa lasketaan ensin kaikkien kärkipisteiden in-aste-arvot.
Aloitetaan sitten kärkipisteestä, jonka in-aste on 0, ja laitetaan se ulostulon loppuun. Kun olemme valinneet pisteen, päivitämme sen viereisten kärkipisteiden in-aste-arvot, koska piste ja sen ulosmenevät särmät poistetaan graafista.
Voidaan toistaa yllä olevaa prosessia, kunnes olemme valinneet kaikki kärkipisteet. Tulostuslista on tällöin graafin topologinen lajittelu.
3.2. Lopputulos. Ajan monimutkaisuus
Kaikkien kärkien in-asteiden laskemiseksi meidän on käytävä kaikissa :n kärkipisteissä ja reunoissa. Siksi in-asteiden laskennan suoritusaika on . Välttääksemme näiden arvojen laskemisen uudelleen, voimme käyttää matriisia pitämään kirjaa näiden kärkipisteiden in-asteiden arvoista. while-silmukan sisällä meidän on myös käytävä kaikissa kärkipisteissä ja reunoissa. Näin ollen kokonaisajoaika on .
Syvyyshaku
Voidaan myös käyttää syvyyshakualgoritmia (Depth First Search, DFS) topologisen lajittelun rakentamiseen.
4.1. Syvyyshaku (Depth First Search). Graafin DFS rekursiolla
Ennen kuin käsittelemme topologisen lajittelun näkökulmaa DFS:n avulla, käymme aluksi läpi vakiomuotoisen, rekursiivisen graafin DFS-kulkualgoritmin:
Vakiomuotoisessa DFS-algoritmissa aloitamme satunnaisesta kärjestä :ssä ja merkitsemme tämän kärjen vierailtuna. Sitten kutsumme rekursiivisesti funktiota dfsRecursive vierailemaan kaikissa sen vierailemattomissa naapuripisteissä. Näin voimme vierailla kaikissa :n kärkipisteissä ajassa.
Mutta koska laitamme jokaisen kärkipisteen listaan heti, kun vierailemme siinä, ja koska voimme aloittaa mistä tahansa kärkipisteestä, tavallinen DFS-algoritmi ei voi taata topologisesti lajitellun listan tuottamista.
Katsotaanpa, mitä pitää tehdä tämän puutteen korjaamiseksi.
4.2. Tehdään näin. DFS-pohjainen topologinen lajittelualgoritmi
Voidaan muokata DFS-algoritmia tuottamaan topologinen lajittelu DAG:lle. DFS-kierroksen aikana, kun kaikki vertexin naapurit on käyty läpi, laitamme sen tuloslistan 
eteen. Näin voimme varmistaa, että esiintyy ennen kaikkia naapureitaan lajitellussa luettelossa:
Tämä algoritmi on samanlainen kuin tavallinen DFS-algoritmi. Vaikka aloitamme edelleen satunnaisesta pisteestä, emme laita pistettä listaan heti, kun käymme sen luona. Sen sijaan käymme ensin rekursiivisesti kaikissa sen naapureissa ja laitamme pisteen sitten listan alkuun. Jos siis sisältää reunan , niin ilmestyy listassa ennen .
Kokonaisajoaika on myös , koska sillä on sama aikakompleksisuus kuin DFS-algoritmilla.
Johtopäätös
Tässä artikkelissa näytimme esimerkin topologisesta lajittelusta DAG:lla. Lisäksi käsittelimme kahta algoritmia, jotka voivat tehdä topologisen lajittelun ajassa.
DFS-pohjaisen topologisen lajittelualgoritmin Java-toteutus on saatavilla artikkelissamme Depth First Search in Java.