Todennäköisyys > Posteriorinen todennäköisyys & posteriorinen jakauma
Mitä on posteriorinen todennäköisyys?
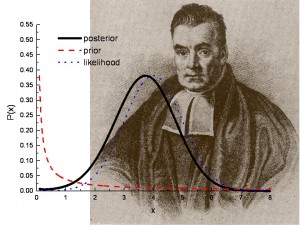
Posteriorisia todennäköisyyksiä käytetään bayesilaisessa hypoteesin testauksessa. Kuva: Los Alamos National Lab.
Posteriorinen todennäköisyys on todennäköisyys, jolla tapahtuma tapahtuu, kun kaikki todisteet tai taustatiedot on otettu huomioon. Se liittyy läheisesti ennakkotodennäköisyyteen, joka on todennäköisyys, että tapahtuma tapahtuu ennen kuin kaikki uudet todisteet on otettu huomioon. Voit ajatella jälkitodennäköisyyttä ennakkotodennäköisyyden mukautuksena:
Historialliset tiedot viittaavat esimerkiksi siihen, että noin 60 % korkeakoulun aloittavista opiskelijoista valmistuu kuuden vuoden kuluessa. Tämä on ennakkotodennäköisyys. Uskot kuitenkin, että tuo luku on todellisuudessa paljon pienempi, joten lähdet keräämään uutta tietoa. Keräämäsi todisteet viittaavat siihen, että todellinen luku on itse asiassa lähempänä 50 %; tämä on posteriorinen todennäköisyys.
Termien alkuperä
Sanat posterior ja prior tulevat latinan kielen sanoista a priori. Määritelmä sanalle ”a priori” on:
”…liittyvät siihen, mitä voidaan tietää ymmärtämällä, miten tietyt asiat toimivat pikemminkin kuin havainnoimalla” ~ Miriam Webster.
”a priori” vastakohta on a posteriori, joka määritellään seuraavasti:
”… relating to what can be known by observation rather than through an understanding of how certain things work.” ~ Miriam Webster.
Mikä on posteriorinen jakauma?
Posteriorinen jakauma on keino tiivistää se, mitä tiedämme epävarmoista suureista Bayes-analyysissä. Se on yhdistelmä priorijakaumasta ja todennäköisyysfunktiosta, joka kertoo, mitä informaatiota havaittu data (”uusi evidenssi”) sisältää. Toisin sanoen posteriorijakauma tiivistää sen, mitä tiedät sen jälkeen, kun tiedot on havaittu. Uusista havainnoista saadun evidenssin yhteenveto on todennäköisyysfunktio.
Posteriorijakaumat ovat elintärkeitä Bayesian analyysissä. Ne ovat monella tapaa analyysin tavoite ja voivat antaa:
- Intervalliestimaatteja parametreille,
- Piste-estimaatteja parametreille,
- Prediction inference for future data,
- Todennäköisyysarvioita hypoteesillesi.
Stephanie Glen. ”Posterior Probability & the Posterior Distribution” From StatisticsHowTo.com: Elementary Statistics for the rest of us! https://www.statisticshowto.com/posterior-distribution-probability/
——————————————————————————
Tarvitsetko apua kotitehtävän tai kokeen kysymyksen kanssa? Chegg Studyn avulla saat kysymyksiisi vaiheittaiset ratkaisut alan asiantuntijalta. Ensimmäiset 30 minuuttia Chegg-opettajan kanssa ovat ilmaisia!