Röntgendiffraktio on yleinen materiaalien karakterisointitekniikka, jonka avulla voidaan tunnistaa kiteiden orientaatiot ja atomien väliset etäisyydet. Röntgensäteilyä käytetään tähän, koska sen aallonpituus on samalla pituusskaalalla kuin atomien välisten etäisyyksien ja ristikkoparametrien arvot.
Mitä tapahtuu?
Röntgensäteilyä tuotetaan tyhjiöputkessa lämmittämällä volframihehkulankaa sen työfunktion ohi, jolloin se syöksyy ulos elektroneja. Tyhjiöolosuhteet ovat välttämättömät, jotta elektronien keskimääräinen vapaa matka kasvaa. Elektronit kiihdytetään kuparikatodiin noin 25 keV:n energialla. Elektronien törmäykset kuparikatodin kanssa johtavat kuoren sisäisiin ionisaatioihin, jotka tuottavat röntgensäteilyä, kun korkeamman energian omaavat elektronit putoavat täyttämään matalamman energian omaavaa tyhjää tilaa. Eri korkeampien energiatasojen elektronit putoavat, jolloin syntyy vaihtelevan energian sähkömagneettisia aaltoja. Näin syntyy röntgensäteilyä useilla aallonpituuksilla (tyyppiä K-beta ja K-alfa). Röntgendiffraktiota varten on ihanteellista, että näytteen kanssa vuorovaikutuksessa oleva valo on monokromaattista, joten K-beta-röntgensäteet suodatetaan pois nikkelilevyllä. Vaikka K-alfa-energioita on tosiaan kaksi, energiat ovat niin samankaltaisia, että se ei vaikuta merkittävästi huippujen kokonaisprofiiliin. Röntgensäteet kulkevat kollimaattorin läpi säteen leveyden säätämiseksi.
Hieman taustaa Braggin laista
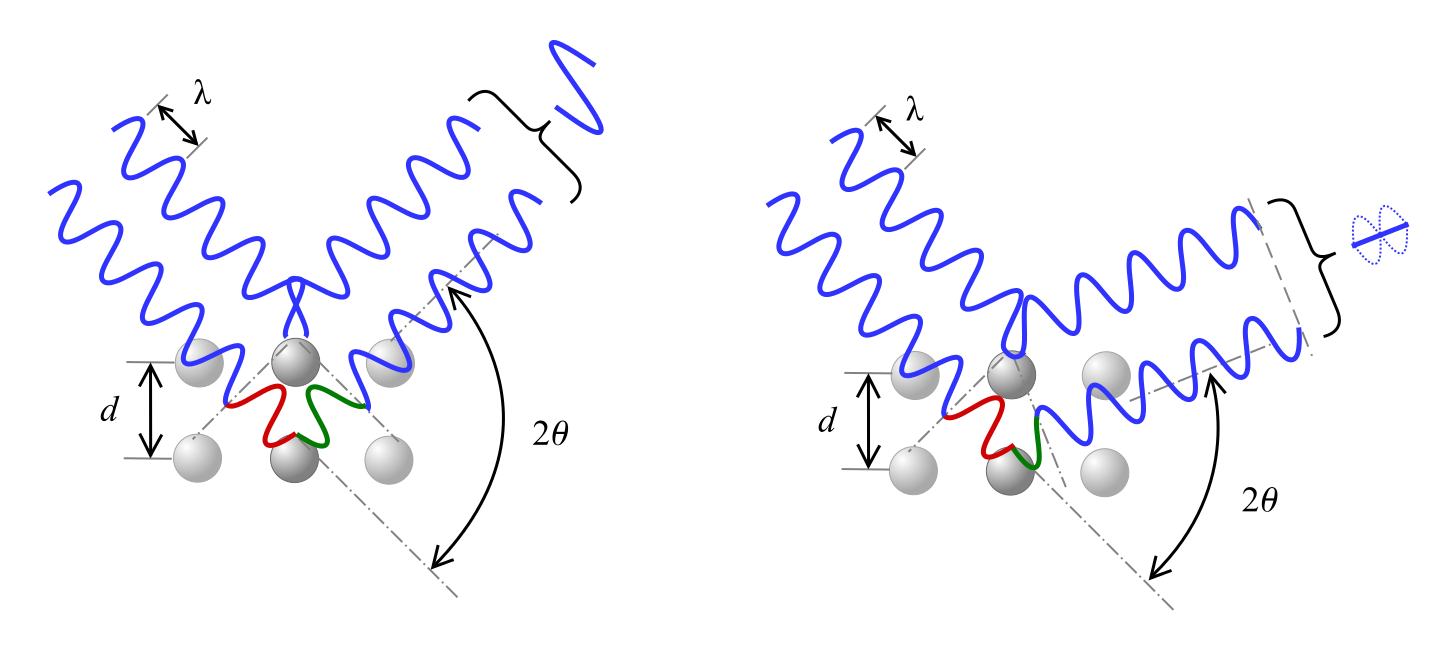
Braggin laki kuvaa suhdetta konstruktiiviselle interferenssille, jossa materiaaliin kulmassa θ osuvat röntgensäteet, joiden aallonpituus λ on aaltopituus λ, diffraktoituvat kiteisiin tasoihin, jotka on erotettu toisistaan etäisyyksellä d, ja jossa n edustaa kokonaisuutta.
Kuten nähdään alla, aallon vaiheensiirto aiheuttaa 2θ-kulman mukaan joko konstruktiivisen interferenssin, kuten vasemmalla on esitetty, tai destruktiivisen interferenssin, kuten oikealla on esitetty.
Yhtälöt XRD-tulosten tulkintaan
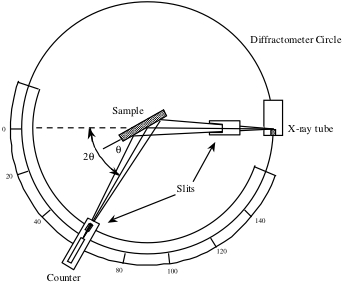
Laskuria, joka näkyy alla röntgendiffraktometrin kaaviokuvassa, kierretään 2θ-arvojen alueella ja se rekisteröi kiteestä heijastuneen röntgensäteilysignaalin intensiteetin kussakin asennossa. Tätä 2θ:n funktiona mitattua intensiteettiä käytetään piikkiprofiilin muodostamiseen.
Kulmissa, jotka täyttävät Bragg-ehdon, havaitaan röntgensäteilysignaalin piikki, joka johtuu konstruktiivisesta interferenssistä. Näitä piikkejä käytetään sitten kidesuuntien tunnistamiseen ja ristikkoparametrien laskemiseen. Kuutiosysteemeille tasoväli d voidaan laskea seuraavalla yhtälöllä, joka on johdettu kiteen geometriasta, jossa a on ristikkoparametri ja h, k ja l ovat Millerin indeksit.
Yhdistämällä Braggin laki ja tasoväli saadaan seuraava yhtälö.
Tässä olemme siirtäneet kaikki vakiot yhtälön vasemmalle puolelle, jolloin voimme verrata sin2(θ)-arvojen ja Miller-indeksien suhteita eri piikkien välillä.
Kun tuleva sähkömagneettinen aalto osuu näytemateriaaliin, materiaalissa olevat elektronit häiriintyvät värähteleväksi kuvioksi, joka synnyttää uutta röntgensäteilyä ja sirottaa tehokkaasti tulevia valoaaltoja. Sironta on kahdenlaista: koherentissa eli elastisessa sironnassa on mukana tiukasti sidottuja värähteleviä elektroneja, jotka sirottavat saman aallonpituuden omaavia röntgensäteitä, ja epäkoherentissa sironnassa löyhästi sidottuja elektroneja asetetaan värähtelevään liikkeeseen ja ne synnyttävät eri energian omaavia röntgensäteitä. Röntgendiffraktio mittaa koherentisti sironneen röntgensäteilyn intensiteettiä, jonka huippu on siellä, missä aallot interferoivat rakentavasti. Atomin sirontakerroin voidaan määritellä atomista sironneen aallon amplitudin ja yksittäisen elektronin sironneen aallon amplitudin suhteena. Tämä suhde kuvaa olennaisesti atomin sirontatehokkuutta tietyssä suunnassa.
Esimerkki XRD-datasta
Tässä on dataa, joka on kerätty kokeesta, jonka tein laboratoriokurssin aikana yrittäessäni tunnistaa tuntematonta metallia sen kiderakenteen perusteella.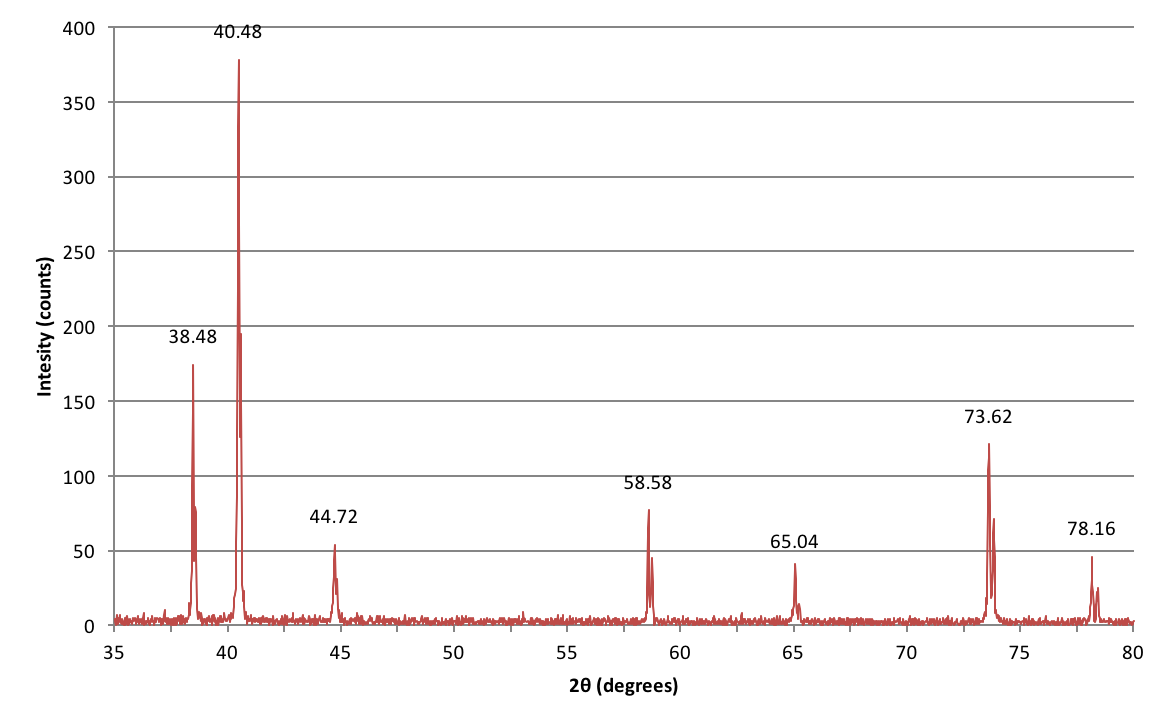
Miten tulkitsen näitä piikkejä?
| Kiderakenne | Edellytykset |
|---|---|
| Simple Cubic | kaikki h, k, l:n arvojen |
| Vartalokeskeisen kuution | h+k+l:n on oltava parillisia |
| Pintakeskeisen kuution | h, k:n ja l:n on oltava kaikki parittomia tai kaikki parillisia |
Rakennetekijät ottavat huomioon tapaukset, joissa taso voi olla kahden viereisen tason puolivälissä ja aiheuttaa destruktiivista interferenssiä. Näiden tekijöiden tuloksena syntyy joukko sääntöjä erilaisille kiderakennegeometrioille, jotka määrittävät, milloin rakentavaa interferenssiä voi esiintyä. Yllä olevassa taulukossa luetellaan Millerin indeksiparametrit, joissa esiintyy rakentavaa interferenssiä. Jäljempänä esitetään laajempi taulukko. Vertailemalla eri diffraktiohuippujen sin2θ-suhteita (toisessa taulukossa $Q^2$) voidaan määrittää kiderakenne ja Miller-indeksit.
| Kiteellinen taso (hkl) | $Q^2$ | Tilaverkot, joista heijastukset ovat mahdollisia | ||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 100 | 1 | SC | ||||||||||||||||||||||||
| 110 | 2 | SC | BCC | 2 | SC | BCC | 2 | 1 | 3 | SC | FCC | DC | ||||||||||||||
| 200 | 4 | SC | BCC | FCC | ||||||||||||||||||||||
| 210 | 5 | SC | ||||||||||||||||||||||||
| 211 | 6 | SC | BCC | |||||||||||||||||||||||
| – | 7 | |||||||||||||||||||||||||
| 220 | 8 | SC | BCC | FCC | DC | |||||||||||||||||||||
| 300, | 311 | 11 | SC | FCC | DC | |||||||||||||||||||||
| 222 | 12 | SC | BCC | FCC | FCC | |||||||||||||||||||||
| – | 15 | 15 | 15 | |||||||||||||||||||||||