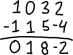Palaa oppituntien hakemistoon | Tee oppitunnit järjestyksessä | Tulosta helppokäyttöinen sivu
Matriisirivioperaatiot (sivu 1 2:sta)
”Operaatiot” on matemaattis-ranskaalinen termi ”proseduuri”. Neljä ”perusoperaatiota” luvuille ovat yhteenlasku, vähennyslasku, kertolasku ja jakolasku. Matriiseille on kolme perusrivioperaatiota; eli on kolme toimenpidettä, joita voit tehdä matriisin riveillä.
Ensimmäinen operaatio on rivinvaihto. Annetaan esimerkiksi matriisi:

…voit vaihtaa rivejä ympäri, jolloin matriisi saadaan mukavampaan rivijärjestykseen, esimerkiksi näin:
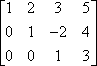
Rivinvaihto ilmaistaan usein piirtämällä nuolia, esimerkiksi näin:

Vaihtaessasi rivejä ympäri varo kopioimasta merkintöjä oikein.
Kakkonen operaatio on rivien kertominen. Annetaan esimerkiksi seuraava matriisi:

…voit kertoa ensimmäisen rivin -1:llä saadaksesi positiivisen etumerkin ensimmäiselle riville:
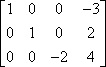
Tämä rivikertolasku ilmoitetaan usein käyttämällä nuolta, jonka yläpuolella on lueteltu kertolasku, esimerkiksi näin:
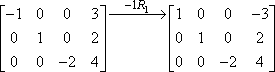
”-1R1” ilmaisee varsinaista operaatiota. ”-1” kertoo, että kerroimme negatiivisella ykkösellä; ”R1” kertoo, että työskentelimme ensimmäisen rivin kanssa. Huomaa, että toinen ja kolmas rivi kopioitiin muuttumattomina toiseen matriisiin. Kertolasku koski vain ensimmäistä riviä, joten kahden muun rivin merkinnät vain siirrettiin muuttumattomina.
Voit kertoa millä tahansa. Esimerkiksi saadaksesi edellisen matriisin kolmannelle riville etummaisen 1:n, voit kertoa kolmannen rivin negatiivisella puolitoistakertaisella:

Koska et tehnyt mitään ensimmäiselle ja toiselle riville, nämä merkinnät vain kopioitiin muuttumattomina uuteen matriisiin.
Voit tehdä useamman kuin yhden rivin kertolaskun samassa vaiheessa, joten olisit voinut tehdä kaksi edellä mainittua vaihetta yhdessä vaiheessa, esimerkiksi näin:
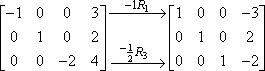
On hyvä käyttää jonkinlaista merkintätapaa (kuten yllä olevia nuolia ja alaindeksejä), jotta voit pitää kirjaa työstäsi. Matriisit ovat hyvin sotkuisia, varsinkin jos teet niitä käsin, ja muistiinpanot voivat helpottaa työsi tarkistamista myöhemmin. Se tekee myös vaikutuksen opettajaan.
Viimeinen rivioperaatio on rivien yhteenlasku. Rivien yhteenlasku on samanlainen kuin lineaaristen yhtälösysteemien ratkaisemisessa käytettävä ”yhteenlasku”-menetelmä. Oletetaan, että sinulla on seuraava yhtälösysteemi:
x + 3y = 1
-x + y = 3 Copyright © Elizabeth Stapel 2003-2011 Kaikki oikeudet pidätetään
Lisäys
Voisit aloittaa tämän systeemin ratkomisen laskemalla sarakkeita alaspäin yhteen saadaksesi arvon 4y = 4:
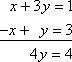
Voit tehdä jotain vastaavaa matriisien kanssa.Jos esimerkiksi annetaan seuraava matriisi:

… voit ”pienentää” (saada enemmän etunollia toiselle riville) lisäämällä siihen ensimmäisen rivin (yleisenä tavoitteena matriisien kanssa tässä vaiheessa on saada jokaisen matriisirivin alkuun ”1” – tai ”0:t” ja sitten ”1”). Kun vähensit kahden yhtälön lineaarista järjestelmää lisäämällä, piirsit ”yhtäsuuruus”-palkin alareunan poikki ja lisäsit alaspäin. Kun käytät yhteenlaskua matriisissa, sinun on otettava mukaan raaputuspaperia, koska et halua yrittää tehdä työtä matriisin sisällä. Lisää siis kaksi riviä raaputuspaperillesi:
|
Scratch work – |
|
Tämä on uusi toinen rivisi; kirjoitat sen vanhan kakkosrivin paikalle. Tulos näyttää tältä:
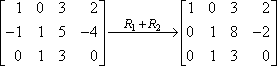
Tässä tapauksessa nuoli ”R1 + R2” tarkoittaa ”Lisäsin ensimmäisen rivin toiseen riviin, ja tämän tuloksen sain”. Koska ykkösrivi ei oikeastaan muuttunut, ja koska emme tehneet mitään kolmosriville, nämä rivit kopioidaan uuteen matriisiin muuttumattomina.
Top | 1 | 2 | Palaa hakemistoon Seuraava >>
|
Lainaa tätä artikkelia seuraavasti: |
. |