Luokittelu diskriminaatioanalyysin avulla
Katsotaan, miten LDA voidaan johtaa valvotuksi luokittelumenetelmäksi. Tarkastellaan yleistä luokitusongelmaa: Satunnaismuuttuja X kuuluu johonkin K:sta luokasta, jolla on joitakin luokkakohtaisia todennäköisyystiheyksiä f(x). Diskriminointisääntö pyrkii jakamaan data-avaruuden K erilliseen alueeseen, jotka edustavat kaikkia luokkia (kuvittele ruutuja shakkilaudalla). Näiden alueiden avulla luokittelu diskriminanttianalyysin avulla tarkoittaa yksinkertaisesti sitä, että luokittelemme x:n luokkaan j, jos x on alueella j. Kysymys kuuluukin, mistä tiedämme, mihin alueeseen data x kuuluu? Voimme luonnollisesti noudattaa kahta allokointisääntöä:
- Maximum likelihood -sääntö: Jos oletamme, että kukin luokka voisi esiintyä yhtä suurella todennäköisyydellä, allokoi x luokkaan j, jos
- Bayesin sääntö: Jos tiedämme luokkien ennakkotodennäköisyydet π, niin allokoidaan x luokkaan j, jos

Lineaarinen ja kvadraattinen diskriminanttianalyysi
Jos oletetaan datan tulevan monimuuttujaisesta gaussilaisesta jakaumasta, i.ts. X:n jakaumaa voidaan luonnehtia sen keskiarvon (μ) ja kovarianssin (Σ) avulla, saadaan edellä esitetyille jakosäännöille eksplisiittiset muodot. Bayesin säännön mukaisesti luokittelemme datan x luokkaan j, jos sillä on suurin todennäköisyys kaikista K luokasta i = 1,…,K:

Edellä mainittua funktiota kutsutaan nimellä diskriminanssifunktio. Huomaa, että tässä käytetään log-likelihoodia. Toisin sanoen diskriminanssifunktio kertoo, kuinka todennäköisesti data x kuuluu kuhunkin luokkaan. Päätöksentekoraja, joka erottaa mitkä tahansa kaksi luokkaa, k ja l, on siis niiden x:n joukko, joissa kahdella diskriminanttifunktiolla on sama arvo. Näin ollen mikä tahansa aineisto, joka osuu päätösrajalle, on yhtä todennäköisesti kahdesta luokasta (emme voineet päättää).
LDA syntyy tapauksessa, jossa oletamme, että K luokan välillä on yhtäläinen kovarianssi. Toisin sanoen sen sijaan, että jokaisella luokalla olisi yksi kovarianssimatriisi, kaikilla luokilla on sama kovarianssimatriisi. Tällöin saadaan seuraava diskriminanssifunktio:

Huomaa, että tämä on lineaarinen funktio x:ssä. Näin ollen myös minkä tahansa luokkaparin välinen päätöksentekorajapinta-ala on lineaarinen funktio x:ssä, mistä johtuen myös analyysimenetelmän nimitys on: lineaarinen diskriminanttilaskenta. Ilman yhtäläisen kovarianssin oletusta todennäköisyyden kvadraattinen termi ei kumoudu, joten tuloksena saatava diskriminanttifunktio on kvadraattinen funktio x:ssä:

Tässä tapauksessa päätöksentekoraja on kvadraattinen x:ssä. Tätä kutsutaan kvadraattiseksi diskriminanttianalyysiksi (QDA).
Kumpi on parempi? LDA vai QDA?
Todellisissa ongelmissa populaatioparametrit ovat yleensä tuntemattomia ja ne estimoidaan harjoitusaineistosta otoskeskiarvoina ja otoskovarianssimatriiseina. Vaikka QDA:ssa on joustavammat päätösrajat kuin LDA:ssa, estimoitavien parametrien määrä kasvaa myös nopeammin kuin LDA:ssa. LDA:n tapauksessa tarvitaan (p+1) parametria (2) diskriminantifunktion rakentamiseksi. Ongelmassa, jossa on K luokkaa, tarvitaan vain (K-1) tällaista diskriminaattista funktiota valitsemalla mielivaltaisesti yksi luokka perusluokaksi (vähentämällä perusluokan todennäköisyys kaikista muista luokista). Näin ollen LDA:n estimoitavien parametrien kokonaismäärä on (K-1)(p+1).
Toisaalta kullekin QDA:n diskriminanttifunktiolle (3) on estimoitava keskivektori, kovarianssimatriisi ja luokkapriori:
– Keskiarvo: p
– Kovarianssi: p(p+1)/2
– Luokkaprioriteetti: 1
Vastaavasti QDA:lle on estimoitava (K-1){p(p+3)/2+1} parametria.
Siten LDA:ssa estimoitavien parametrien määrä kasvaa lineaarisesti p:n myötä, kun taas QDA:ssa parametrien määrä kasvaa neliöllisesti p:n myötä. Odotamme, että QDA:lla on huonompi suorituskyky kuin LDA:lla, kun ongelman ulottuvuus on suuri.
Kahdesta maailmasta paras? Kompromissi LDA:n & QDA:n
Voidaan löytää kompromissi LDA:n ja QDA:n välille regularisoimalla yksittäisten luokkien kovarianssimatriisit. Regularisointi tarkoittaa, että asetamme estimoiduille parametreille tietyn rajoituksen. Tällöin edellytämme, että yksilöllinen kovarianssimatriisi kutistuu kohti yhteistä yhdistettyä kovarianssimatriisia rangaistusparametrin avulla, esim. α:

Yhteistä kovarianssimatriisia voidaan regularisoida rangaistusparametrin avulla kohti identtisyyttä osoittavan matriisin avulla myös esim, β:

Tilanteissa, joissa syötemuuttujien lukumäärä ylittää huomattavasti näytteiden lukumäärän, kovarianssimatriisi voi olla huonosti estimoitu. Kutistamisella voidaan toivottavasti parantaa estimointi- ja luokittelutarkkuutta. Tätä havainnollistaa alla oleva kuva.

Laskenta LDA:lle
Voidaan nähdä kohdista (2) ja (3), että diskriminanttifunktioiden laskentaa voidaan yksinkertaistaa, jos ensin diagonalisoidaan kovarianssimatriisit. Toisin sanoen tiedot muunnetaan siten, että niillä on identtinen kovarianssimatriisi (ei korrelaatiota, varianssi 1). LDA:n tapauksessa menetellään laskennassa seuraavasti:

Vaiheessa 2 sfääritään dataa siten, että saadaan identtinen kovarianssimatriisi muunnetussa avaruudessa. Vaihe 4 saadaan noudattamalla (2).
Katsotaanpa kahden luokan esimerkkiä, jotta nähdään, mitä LDA todella tekee. Oletetaan, että on kaksi luokkaa, k ja l. Luokittelemme x:n luokkaan k, jos

Ylläoleva ehto tarkoittaa, että luokka k on todennäköisempi tuottamaan datan x:n kuin luokka l. Edellä esitettyjen neljän vaiheen jälkeen kirjoitetaan
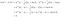
Tämä on, luokittelemme datan x luokkaan k, jos

Ohjattu allokointisääntö paljastaa LDA:n toiminnan. Yhtälön vasen puoli (l.h.s.) on x*:n ortogonaaliprojektion pituus kahta luokkakeskiarvoa yhdistävälle viivapätkälle. Oikeanpuoleinen puoli on segmentin keskipisteen sijainti korjattuna luokkien ennakkotodennäköisyyksillä. Pohjimmiltaan LDA luokittelee pallotetut tiedot lähimpään luokkakeskiarvoon. Voimme tehdä tässä kaksi havaintoa:
- Päätöksentekopiste poikkeaa keskipisteestä, kun luokkien ennakkotodennäköisyydet eivät ole samat, eli rajaa työnnetään kohti luokkaa, jolla on pienempi ennakkotodennäköisyys.
- Data projisoidaan luokkakeskiarvojen peittämään tilaan (x*:n kertolasku ja keskiarvojen vähennys säännön l.h.s.:llä). Etäisyysvertailut tehdään sitten tässä avaruudessa.