- Konnektiivisuus on graafiteorian peruskäsite. Se määrittelee, onko graafi kytkeytynyt vai kytkeytymätön. Ilman kytkeytyneisyyttä ei ole mahdollista kulkea graafissa yhdestä pisteestä toiseen pisteeseen.
- Graafin sanotaan olevan kytkeytynyt graafi, jos jokaisen kärkiparin välillä on polku. Jokaisesta pisteestä mihin tahansa toiseen pisteeseen on oltava jokin polku kuljettavissa. Tätä kutsutaan graafin kytkeytyneisyydeksi.
- Graafin sanotaan olevan kytkeytymätön, jos on olemassa useita kytkeytymättömiä kärkipisteitä ja särmiä.
- Graafin kytkeytyneisyysteoriat ovat välttämättömiä verkkosovelluksissa, kuljetusverkkojen reitityksessä, verkon sietokyvyssä jne.
Esimerkki
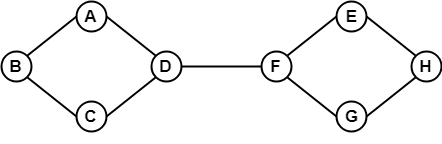
Ylläolevassa esimerkissä on mahdollista kulkea yhdestä kärjestä toiseen. Tässä voidaan kulkea pisteestä B pisteeseen H käyttäen polkua B -> A -> D -> F -> E -> H. Kyseessä on siis kytkeytynyt graafi.
Esimerkki
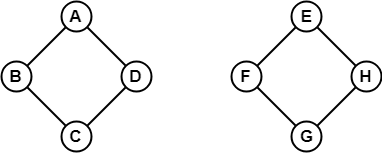
Ylläolevassa esimerkissä ei ole mahdollista kulkea pisteestä B pisteeseen H, koska pisteiden välissä ei ole polkua suoraan tai välillisesti. Näin ollen kyseessä on kytkeytymätön graafi.
Katsotaanpa muutamia kytkeytyneisyyden peruskäsitteitä.
Leikkauspiste
Yksittäistä kärkeä, jonka poistaminen katkaisee graafin yhteyden, kutsutaan leikkauspisteeksi.
Olkoon G kytkeytynyt graafi. G:n kärkeä v sanotaan G:n leikatuksi kärkipisteeksi, jos G-v (Poista v G:stä) antaa tulokseksi irrallisen graafin.
Kun poistamme graafista pisteen, niin graafi hajoaa kahdeksi tai useammaksi graafiksi. Tätä kärkeä kutsutaan leikatuksi kärkipisteeksi.
Huomautus: Olkoon G graafi, jossa on n kärkeä:
- Yhteenkytketyllä graafilla G voi olla maksimissaan (n-2) leikattua kärkeä.
- Leikatun kärkipisteen poistaminen voi jättää graafin irralliseksi.
- Pisteen poistaminen voi lisätä graafin komponenttien määrää vähintään yhdellä.
- Puun jokainen ei-riippuvainen piste on leikattu piste.
Esimerkki 1

Esimerkki 2
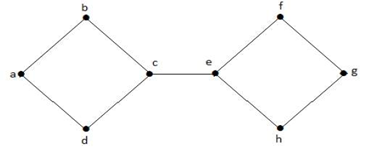
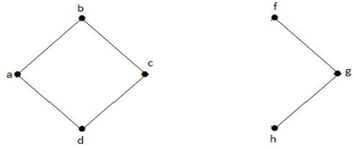
Ylläolevassa graafissa piste ’e’ on leikattu piste. Kun edellä olevasta kuvaajasta on poistettu piste ’e’, kuvaajasta tulee epäyhtenäinen kuvaaja.
Leikkaussärmä (silta)
Leikkaussärmä eli silta on yksittäinen särmä, jonka poistaminen epäyhtenäistää kuvaajan.
Olkoon G yhdistetty kuvaaja. G:n reunaa e kutsutaan G:n leikatuksi reunaksi, jos G-e (Poista e G:stä) saa tulokseksi irrallisen graafin.
Kun poistamme graafista reunan, niin graafi hajoaa kahdeksi tai useammaksi graafiksi. Tätä poistettavaa reunaa kutsutaan leikatuksi reunaksi tai sillaksi.
Huomautus: Olkoon G graafi, jossa on n kärkeä:
- Yhteenkytketyllä graafilla G voi olla korkeintaan (n-1) leikattua reunaa.
- Leikatun reunan poistaminen voi jättää graafin irralliseksi.
- Reunan poistaminen voi lisätä graafin komponenttien lukumäärää korkeintaan yhdellä.
- Loikattu reuna ’e’ ei saa olla minkään syklin osa G:ssä.
- Jos on olemassa leikattu reuna, on oltava olemassa myös leikattu kärki, koska vähintään yksi leikatun reunan kärki on leikattu kärki.
- Jos leikattu huippu on olemassa, minkään leikatun reunan olemassaolo ei ole välttämätöntä.
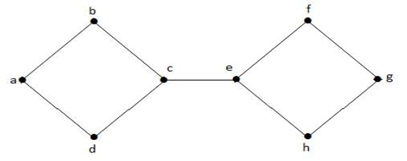
Esimerkki 1
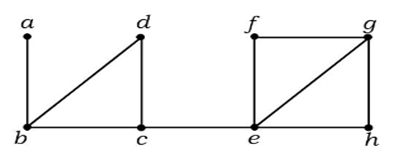
Yllä olevassa graafissa reuna (c, e) on leikattu reuna. Kun tämä reuna on poistettu yllä olevasta kuvaajasta, kuvaajasta tulee irrallinen kuvaaja.
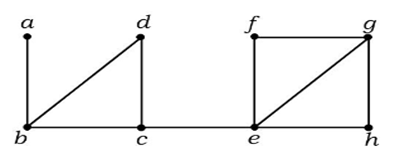
Esimerkki 2
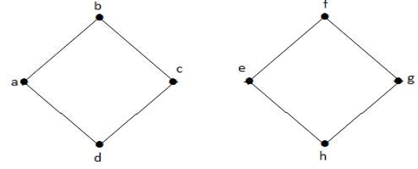
Yllä olevassa kuvaajassa reuna (c, e) on leikattu reuna. Kun tämä reuna on poistettu yllä olevasta graafista, graafista tulee epäyhtenäinen graafi.
Leikkausjoukko
Yhteenliittyneessä graafissa G leikkausjoukko on särmien joukko S, jolla on seuraavat ominaisuudet:
- Kaikkien S:ssä olevien särmien poistaminen irrottaa G:n.
- Joidenkin S:n reunojen (mutta ei kaikkien) poistaminen ei katkaise G:tä.
Esimerkki 1
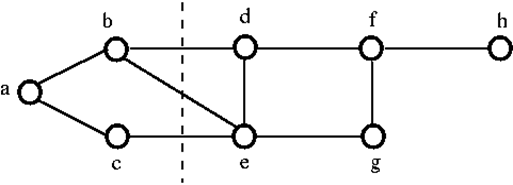
Kun haluamme katkaista yllä olevan graafin G, meidän on poistettava kolme reunaa. eli bd, be ja ce. Emme voi irrottaa sitä poistamalla vain kaksi kolmesta reunasta. Näin ollen {bd, be, ce} on leikattu joukko.
Poistettuamme leikatun joukon yllä olevasta graafista, se näyttäisi seuraavalta:
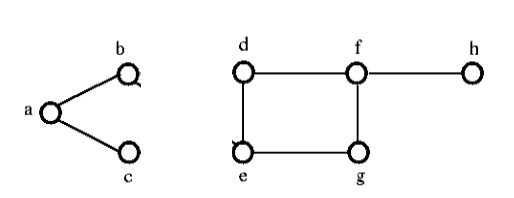
Edge Connectivity
Yhteen kytketyn graafin G reunojen kytkeytyvyys on niiden reunojen vähimmäismäärä, joiden poistaminen tekee G:stä kytkemättömän. Sitä merkitään λ(G):llä.
Kun λ(G) ≥ k, niin graafin G sanotaan olevan k-särmäyhteinen.
Esimerkki
Katsotaan esimerkki,
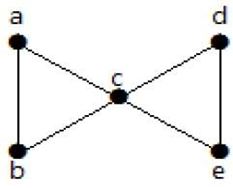
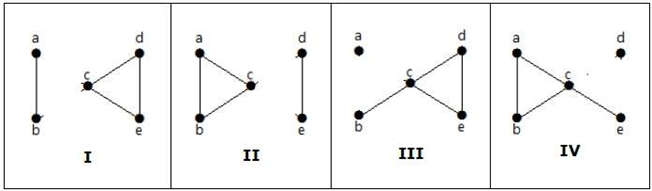
Yllä olevasta graafista, poistamalla kaksi minimireunaa, kytketty graafi muuttuu kytkemättömäksi graafiksi. Näin ollen sen reunakytkeytyneisyys on 2. Näin ollen yllä oleva graafi on 2-särmäisesti kytkeytynyt graafi.
Tässä on seuraavat neljä tapaa kytkeä graafi irti poistamalla kaksi reunaa:
Pisteiden kytkeytyneisyys
Kytkeytyneen graafin G kytkeytyneisyys (tai pisteiden kytkeytyneisyys) on pienin mahdollinen määrä kärkipisteitä, joiden poistaminen saa G:n irti kytkeytyneeksi tai redusoituneeksi triviaaleiksi graafeiksi. Sitä merkitään K(G):llä.
Graafin sanotaan olevan k-kytketty tai k-pisteen kytketty, kun K(G) ≥ k. Poistaaksemme jonkin pisteen meidän on poistettava myös siihen osuvat särmät.
Esimerkki
Katsotaan esimerkki:
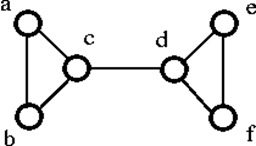
Yllä oleva graafi G voidaan katkaista poistamalla yksittäinen huippu joko ’c’ tai ’d’. Näin ollen sen pisteiden kytkeytyvyys on 1. Se on siis 1-kytkeytynyt graafi.