How Many Sides Does A Circle Have?

Se on peruskoulun läksykysymys, joka aiheuttaa erimielisyyttä kokeneiden matemaatikkojen keskuudessa. Löytääkseni oikean vastauksen turvauduin tuohon tiukimpaan tieteelliseen välineeseen, Twitter-kyselyyn:

Jälkikäteen pahoittelen, etten ottanut mukaan vaihtoehtoa ”ei mikään edellä mainituista”, mutta siitä lisää myöhemmin. Tässä postauksessa käyn läpi nämä kolme vastausta (ja ”Ei mikään edellä mainituista”) ja keskustelen niiden hyvistä ja huonoista puolista näkemykseni mukaan, ennen kuin paljastan dramaattisesti oikean vastauksen.

Mutta ensin: miksi emme voi antaa suoraviivaisesti oikeaa vastausta? Kysymyksen sanat tuskin ovat salaperäisiä. Me kaikki tiedämme, mikä on ”ympyrä”, mitä tarkoittaa laskea ”kuinka monta” jotain ja mikä on ”sivu”… vai tiedämmekö? Tässä ovat (karkeat) määritelmät, jotka sain kahden peruskoululaisen kanssa käydyistä keskusteluista, jotka olivat joutuneet tämän kysymyksen kohteeksi:

1. Viiva, joka muodostaa osan tasokuvion muodon rajasta.

Tarkoitus sanoa tässä tasokuvio eikä ”muoto” on, että haluamme muodot, jotka elävät kaksiulotteisesti (esim. neliöt tai ympyrät, mutta ei pallot tai kuutiot). Seuraava kysymys on, mikä on ”viiva” määritelmässä 1. Tässä on muunnelma, joka määrittää sen:

2. Suora viiva, joka muodostaa osan tasokuvion rajasta.

Jos kirjoitat Googleen ”define: side”, olennaisin määritelmä on:

Suoraviivainen luku on suorista viivoista rakennettu luku. Tämä määritelmä on siis määritelmän 2 jatkojalostus, ja sen avulla voimme vakuuttaa, että neliöllä on neljä sivua, mutta se ei päällisin puolin sano mitään ei-suoralinjaisista tasokuvioista, kuten ympyröistä.

Ilman äärettömän monta sivua?

Luulen, että Twitter-kyselyyni vastanneiden matemaattisen sivistyksen taso on varmasti korkeampi kuin maan keskiarvo. Se, että he ylipäätään jakaantuivat tässä kysymyksessä ja että pieni enemmistö valitsi vastauksen, jota tämän kysymyksen tavalliselle kohderyhmälle (peruskoululaiset) ei ole aika hyvin saatavilla, viittaa varmasti siihen, että jossain on mennyt jotain pieleen.

Onko ympyrällä siis äärettömän monta sivua? On varmasti hyödyllistä pitää ympyrää n-sivuisten monikulmioiden rajana, kun n kasvaa yhä suuremmaksi. Juuri tätä lähestymistapaa Arkhimedes, Liu Hui ja lukemattomat muut ovat vuosisatojen saatossa käyttäneet ympyrän geometrian tutkimiseen, mukaan lukien π:n approksimaatioiden keksiminen.

Kolmannella vuosisadalla jKr. julkaistun Jiuzhang suanshun (Yhdeksän lukua matemaattisesta taidosta) 1500-luvun Ming-dynastian painos.

Joskus on täysin järkevää ajatella ympyrän olevan kuin monikulmio, jolla on äärettömän monta sivua.

Mutta sietämättömänä pedanttina matemaatikkona haluaisin erottaa toisistaan kätevän pikakirjoituksen ja kirjaimellisen totuuden. Jos olemme vakaasti sitä mieltä, että ympyrä todella on monikulmio, jolla on äärettömän monta sivua, niin silloin herää kysymys: mitkä ovat sivut? Ja varmasti ainoa uskottava vastaus on: ympyrän yksittäiset pisteet. Kuinka pitkiä nämä niin sanotut sivut ovat? Nolla senttimetriä. Ja ovatko nämä sivut erotettu toisistaan kulmilla? Ei ilmeisesti, joko kulmia ei ole lainkaan, tai jokainen piste on sekä sivu että kulma.

Sanoisin, että sivut, joiden pituus on nolla, ovat… ongelmallinen käsite. Mistä voi päätellä onko niitä yhtään? Oletetaan esimerkiksi, että tutkin systeemiä, jossa neliö syntyy kahdeksankulmioiden raja-arvona näin:

Tässä tilanteessa voisi hyvinkin olla järkevää ajatella, että neliölläni on kahdeksan sivua, joista neljällä on pituus nolla. Mutta jos väittäisin, että (täysin tavallisella) neliölläni todella on kahdeksan sivua, saattaisit ehkä kohottaa kulmakarvoja.

Tämä – äänestykseni voittajavastaus – on siis ainoa vastaus, jonka aion julistaa lopullisesti vääräksi, samalla kun se on myös ainoa, joka tarjoaa minkäänlaista geometrista oivallusta. Paradoksi? Ei oikeastaan. Analoginen päättely on arvokas taito matematiikassa ja elämässä; samalla on tärkeää pitää kiinni siitä, että ymmärrämme, että juuri sitä me teemme.

Jos on äärettömän monta puolta: geometrisesti valaisevaa.
Jos äärettömän monta sivua: kahdeksansivuiset neliöt.

Tangentilla 1: apeirogonit

Jopa jos ympyrä ei ole sellainen, onko olemassa sellaisia monikulmioita, joilla on äärettömän monta sivua? No, on olemassa sana kuvaamaan sellaista asiaa apeirogon. Säännöllisessä apeirogonissa olisi sitten yhtä pitkät (ei-nolla) sivut ja niiden väliset kulmat olisivat yhtä suuret. Ainoa vaihtoehto tässä on tämä ällistyttävän jännittämätön objekti:

Jos vastustat sitä, että tämä on ”monikulmio” (joko 180°:n kulmien vuoksi tai siksi, että reunojen ketju ei sulkeudu silmukaksi), niin miten olisi jotain tämän kaltaista: aloitetaan ympyrän alareunasta ja kuljetaan jokaisessa vaiheessa puolet siitä, mitä ympyrästä on jäljellä, ja korvataan juuri kuljettu kaari suoralla reunalla:

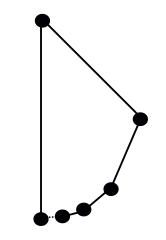
Onko tämä aito monikulmio? Jälleen kerran se riippuu termeistäsi. Yhden yleisen määritelmän, ”suljetun monikulmion ketjun”, mukaan tämä ei kelpaa, koska aloituskulma (alhaalla vasemmalla) liittyy vain yhteen reunaan. Mutta se on hyvin läheltä piti: tuo piste on oikealta tulevan reunojen sarjan raja, mikä tekee tästä muodosta ”ei-itseään leikkaavan paloittain lineaarisen suljetun käyrän”, joka on toinen monikulmion määritelmä, jota ihmiset käyttävät.

Jos jätämme tavanomaisen euklidisen maailmamme ja siirrymme hyperboliseen avaruuteen, niin epäselvyyttä ei ole. Apeirogonit (jopa säännölliset apeirogonit) ovat yksinkertaisesti olemassa:

Hyperbolisen tason laatoitus säännöllisillä apeirogoneilla. (By Anton Sherwood – Own work, Public Domain, https://commons.wikimedia.org/w/index.php?curid=13260274 )

Off on a tangentti 2: ääripisteet

Voi olla perustellumpaa sanoa, että ympyrässä on äärettömän monta kulmaa kuin äärettömän monta sivua (tosin tätä kysymystä ei tunnu kysyttävän kovin usein). Aluksi, jos neliön kulma on piste, jossa sen rajaviiva ei ole suora, niin ympyrän jokainen piste täyttää tämän. Vielä hienostuneemmin on olemassa käsite muodon ääripiste: se on mikä tahansa piste, jonka kautta voidaan piirtää suora, joka koskettaa muotoa vain kyseisessä pisteessä. Neliön ja monien muiden tuttujen muotojen ääripisteet osuvat täsmälleen kulmien kanssa. Jokainen piste ympyrän rajalla on ääripiste, joten on varmasti totta, että ympyrällä on äärettömän monta ääripistettä.

Voisimme huolestua siitä, että joillakin muodoilla, kuten tällä sakaralla, on kulmia, jotka eivät ole ääripisteitä:

Tässä alempi keskuskulma ei ole ääripiste (kolme muuta kulmaa ovat). Se mikä menee pieleen on se, että tämä muoto ei ole kupera (karkeasti sanottuna siinä on joitain kohtia, jotka työntyvät liian pitkälle ulos). Ympyrä on kupera, joten ehkä meidän ei tarvitse olla huolissamme. Vaihtoehtoisesti voimme korjata tilanteen määrittelemällä ”kulman” pisteeksi pisteen, joka on joko kyseisen muodon tai sen komplementin ääripiste, eli koko tason, josta muoto on leikattu pois. Tämä lähestymistapa havaitsisi kaikkien monikulmioiden, myös sakaran, kulmat. Sileiden käyrien osalta se tunnistaisi kaikki rajapisteet ”kulmiksi” lukuun ottamatta taivutuspisteitä (mikä ei ole kohtuutonta, koska voisimme väittää, että raja on siellä suora).

Yksi sivu?

Alkuopetuksessa näyttää siltä, että ”yksi” on vastaus, joka saa rastin. Ja sille on kohtalaisen kelvollinen perustelu. Muistakaa yllä oleva määritelmä 1:

1. Viiva, joka muodostaa osan tasokuvion rajasta.

Välitön kysymys on, mikä lasketaan ”viivaksi”, varsinkin jos emme vaadi suoruutta. Jos suhtaudumme asiaan liian rennosti, minkä tahansa tasokuvion voidaan sanoa omaavan ”yhden sivun”, samassa mielessä kuin sillä on yksi raja, kehä tai kehä. Tämän on kuitenkin oltava väärin, sillä haluamme varmasti, että neliöllä on neljä sivua. No, neliöllä on neljä kohtaa, joissa se ei ole sileä, ja niiden välissä on neljä sileää kohtaa. Ehkä laskimme koko ajan sileitä kohtia. Meillä on siis implisiittisesti uusi tarkennus määritelmään 1 (ja käytämme myös tilaisuutta hyväkseni luopuaksemme epämääräisestä termistä ”hahmo”):

4. Kukin sileä leikkaus kappaleenomaisesti sileästä suljetusta käyrästä.

”Suljettu käyrä” on käyrä, joka kiertyy itseensä niin, että sillä ei ole vapaita päitä. ”Piecewise-smooth” tarkoittaa, että se rakentuu sileistä osista, jotka kohtaavat eristetyissä epäsilevissä pisteissä. On täysin oikeutettua haluta laskea tällaisen muodon reunan sileät osat, eikä ole mitenkään törkeää käyttää sanaa ”sivu” tätä tarkoitusta varten. En siis todellakaan väitä, että tämä olisi lopullisesti väärä vastaus.

Kysymys on, onko tämä tulkinta ”sivusta” paitsi johdonmukainen, myös tarpeeksi luonnollinen, jotta se voidaan yksinkertaisesti olettaa ilman, että se on ilmaistu eksplisiittisesti (mitä se harvoin, jos koskaan, on). Mitä tapahtuu, kun sileys ja suoruus täsmäävät eri tavalla? Tarkastellaanpa tätä hautakiven muotoa, joka on luotu korvaamalla neliön yläosa halkaisijaltaan yhtä suurella puoliympyrällä.

Tässä on kaksi sileää osaa (alaviiva ja loppuosa), mutta kolme suoraa reunaa (ja lisäksi kaareva pala, joka yhdistää sujuvasti kaksi niistä). Kuinka monta sivua sillä siis on? Konsultoin taas Twitter-kavereitani:

Tällä kertaa minun olisi pitänyt ottaa vaihtoehdoksi ”äärettömän monta”, vaikka se voikin sulautua kohtaan ”Ei mikään edellä mainituista”. Jokaisen, joka äänestää, että ympyrällä on äärettömän monta sivua, pitäisi automaattisesti äänestää tässä ”Ei mikään edellä mainituista”, ellei – tärkeä varoitus – tämän muodon luonne osoita lukijalle toisenlaista käsitystä ”sivusta”. Se, että suosituimmat vaihtoehdot näissä kahdessa äänestyksessä ovat yhteensopimattomia, viittaa siihen, että näin saattaa olla (tai ainakin vahvistaa sitä, että vedet ovat epäselvät).

Vaikka kaksi on täysin hyväksyttävä vastaus, joka on yhteensopiva edellä olevan määritelmän 4 ja ympyrän yksipuolisuuden kanssa, en ole vakuuttunut siitä, että se on lopullisesti oikea, tai siitä, että kolme tai neljä ovat kategorisesti väärin. Riippuu siitä, mitä halutaan laskea: sileitä osia, suoria reunoja vai suoria reunoja ja mitä tahansa jäljelle jääviä osia, joista mikä tahansa voi olla haluttu vastaus asiayhteydestä riippuen (tästä lisää jäljempänä). Tähän liittyen en ole varma, että sileiden osien lukumäärän laskeminen vastaa täysin intuitiotani sanasta ”sivu”. Loppujen lopuksi hautakiven kaksi pystysuoraa osiota ovat – mielestäni on perusteltua sanoa – ”vastakkaisilla puolilla”. Olemmeko todella tyytyväisiä siihen, että ne ovat samanaikaisesti osa ”samaa puolta”?

Voit ehkä protestoida, että sekoitan ”puolen” kaksi erilaista merkitystä, että terminologia törmää joskus toisiinsa, ja meidän on vain elettävä sen kanssa. En ole siitä kuitenkaan niin varma. Tämän harjoituksen tarkoitus on ekstrapoloida tilanteesta (suoraviivaiset luvut), jossa nämä kaksi käsitettä sopivat melko hyvin yhteen. Jos olisi olemassa uusi idea, joka sisältäisi kaiken, mistä pidimme alkuperäisessä ideassa, mutta jota sovellettaisiin myös laajempaan ryhmään muotoja, se olisi ylivoimaisesti ainoa oikea vastaus. Mutta jos kaikki yleistämisyrityksemme edellyttävät alkuperäisen muodon toivottujen piirteiden uhraamista, silloin ei ehkä ole olemassa yhtä ainoaa oikeaa yleistystä. On olemassa erilaisia vaihtoehtoja, joilla on erilaisia kompromisseja, jotka saattavat olla sopivia eri yhteyksissä (ja jos olemme tilanteessa, jossa useampi kuin yksi on pelissä, niin niille voitaisiin hyödyllisesti antaa eri nimet).

Tässä on toinen variaatio: Weierstrassin hautakivi, joka on luotu korvaamalla neliön yläreuna osalla Weiestressin funktiota, äärettömän kiemurtelevalla viivalla, joka ei ole sileä missään.

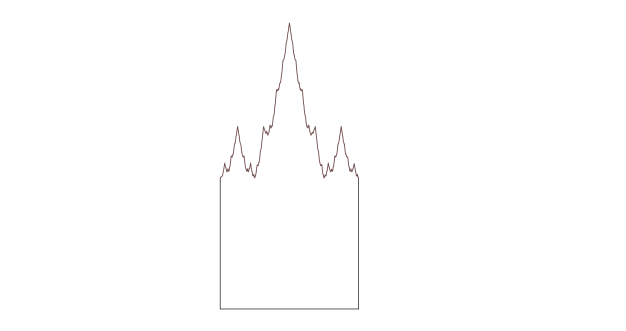
Tässä (ja huomaa kirjoitusvirhe), mitä Twitter-kaverini tekivät tästä – tosin harvempi uskalsi sanoa mielipiteensä:

Twitter-seuraajieni skeptisyydestä huolimatta selitän kohta, miksi mielestäni ei ole hölmöä nähdä, että tällä on neljä sivua (joista yksi ei ole sileä). Toisaalta, jos haluat mieluummin sileät sivut, voit taas valita, näetkö sillä olevan äärettömän monta sivua (joista kolmella on pituus 1 ja lopuilla pituus 0) vai onko sillä kolme sivua ja pätkä ehdottomasti ei-sivua -rajaa.

Yksi sivuksi: yksi sileä käyrä.
Yksi sivuksi: sama sivu vastakkaisilla sivuilla.

Tangentilla 3: sivut vs. reunat

Miten monta sivua neliöllä on? 4. Kuinka monta reunaa sillä on? Neljä. Ovatko reunat ja sivut siis sama asia? Ei välttämättä. Tässä on kaksi konfiguraatiota, jotka ovat – ainakin väitetysti – kumpikin nelisivuisia, mutta joilla on 5 ja 3 reunaa:

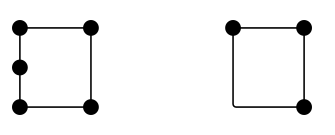
Yleisesti sanoisin, että ”reuna” on topologinen objekti siinä mielessä, että sen funktiolla, ei sen muodolla, on merkitystä. Ajattele vaikka Lontoon metrokarttaa. Jos kysyisit, kuinka monta reunaa tuossa verkossa on, ei ole mitään järkeä laskea yhteen suoria tai sileitä osuuksia. Asemien (tai kärkipisteiden) väliset yhteydet ratkaisevat.

Kuten jo mainittiin, monikulmio on tavallista ajatella hyvin yksinkertaisena verkkona, jota kutsutaan suljetuksi monikulmioketjuksi: joukko kärkipisteitä (tässä tapauksessa monikulmion kulmia), jotka on liitetty toisiinsa särmillä siten, että jokainen kärkipiste sijaitsee täsmälleen kahdella särmällä, ja kokonaisuus muodostaa yhden silmukan. Tässä tilanteessa särmät ja sivut ovat yhtenevät, samoin kuin kärkipisteet ja kulmat. Mutta yleensä tämän yhteneväisyyden voi rikkoa, kuten yllä olevissa kahdessa pienessä verkossa.

Jos haluaa ajatella asioita verkkoteoreettisesti, mutta kärkipisteitä ei ole selvästi merkitty, on arvattava, missä ne ovat. Monikulmion kohdalla tämä on helppoa – kärkipisteet ovat kulmissa – minkä vuoksi vaihtaminen geometrisen ja topologisen lähestymistavan välillä on niin luonnollista. Muiden muotojen, kuten jommankumman edellä esitetyn hautakiven, kohdalla se ei välttämättä ole niin itsestään selvää. Jos teille kuitenkin sanottaisiin, että jossakin on kärkipisteitä, ja teitä pyydettäisiin paikantamaan ne, olisi mielestäni järkevää arvata, että niitä on neljä, nimittäin alkuperäisen neliön kulmat, ja että yläreuna on jostain syystä esitetty epäsuorana viivana. Ja jos haluamme ajatella asioita niin, että jokaisella hautakivellä on neljä reunaa, se saattaa tuntua perverssiltä (vaikkakin loogisesti johdonmukaiselta!).) vaatia, että niillä on jokin muu määrä sivuja (varsinkin kun yläsivu on – omasta geometriastaan huolimatta – selvästi kuvion ”yhdellä sivulla”). Itse asiassa eräs Twitter-kirjeenvaihtajani kysyi arvailun sijaan minulta: ”Onko molemmat ylimmät kärkipisteet poistettu?” Kysymys, joka on järkevä vain verkkoteoreettisesta näkökulmasta.

Mihin tämä jättää ympyrän? Ongelmana on se, että millään ympyrän pisteellä ei ole parempaa oikeutta olla piste kuin millään muulla. Joten vaikka on houkuttelevaa (ja taas johdonmukaista) tarkastella ympyrää verkostona, jossa on yksi reuna, jos aiomme lisätä kärkipisteitä, ei ole mitään ilmeistä syytä suosia yhtä numeroa jonkin muun numeron sijasta.

Voisimmeko tarkastella sitä verkostona, jossa ei ole lainkaan kärkipisteitä, eräänlaisena metrolinjana, jossa ei ole asemia? Tavallinen matemaattinen käsitys verkosta ei sallisi sitä, mutta sen ei pitäisi estää meitä liikaa. Tämä viittaa puhtaasti topologiseen lähestymistapaan. Ongelmana on, että tästä näkökulmasta katsottuna ympyrä voi olla eräänlainen verkko, jossa ei ole kärkipisteitä ja jossa on vain yksi reuna, mutta myös neliö on sellainen (jos metrolinja sattuu olemaan sellainen). Topologiassa neliö on ympyrä. (Tämä ei ole paradoksi, vaan yksinkertaisesti sanotaan, että raja on yksi silmukka, jonka muodolla ei ole väliä). Vaikka tällaisella verkolla on ”yksi reuna”, neliöllä ei tietenkään ole ”yhtä sivua”, joten sivujen (geometristen) ja reunojen (topologisten) välinen suhde on jälleen hajonnut, aivan kuten edellä kuvatuissa kahdessa pienessä verkossa. Tämä lähestymistapa ei siis vie meitä kovin pitkälle.

Ei sivuja?

Saattaa tuntua paradoksaaliselta väittää, että ympyrällä (tai millä tahansa muodolla) ei ole ”sivuja”. Mutta argumentti puolustuksen puolesta on suoraviivainen. Palataan määritelmään 2:

2. Suora viiva, joka muodostaa osan tasokuvion rajasta.

Tämä on yksinkertainen, helposti ymmärrettävä lause, joka kuvaa täydellisesti neliön sivuja. Emme ole onnistuneet löytämään tälle tyydyttävää yleistystä kaareviin kuvioihin, joten on parasta pitäytyä alkuperäisessä. Ja ympyrässä ei ole sivuja.

Ei ole sivuja: totta, järkevän ”sivun” käsitteen mukaan.
Ei ole sivuja: kuulostaa zen-koanilta.

Ei mitään edellä mainituista?

Palauta mieleen Googlen antama määritelmä:

3. Jokainen niistä viivoista, jotka muodostavat tasaisen suoraviivaisen kuvion rajan.

Yritetään soveltaa tätä ympyrään – ei-suoraviivaiseen kuvioon – ja tuloksena ei ole mitään. Kysymys on yhtä merkityksetön kuin ”Montako sivua maanantailla on?”

Sen vuoksi, että määritelmä 3 on virallisin (ainoa tässä viestissä, jota en ole keksinyt minä tai lapseni), eikö se tee ”Ei mikään edellä mainituista” kategorisesti oikeaksi vastaukseksi? Ehkä. Toisaalta: kun joku esittää meille kysymyksen, hyväntekeväisyysperiaate ehkä vaatii meitä olettamaan, että se on mielekäs, ellemme voi vakuuttavasti osoittaa muuta, ja määritelmät 1, 2, 4 ja muut vaihtoehdot tekevät sen mahdolliseksi. Lisäksi määritelmä 3 on pikemminkin kielellinen kuin muodollisesti matemaattinen ja siksi pikemminkin deskriptiivinen kuin preskriptiivinen, joten meidän ei pitäisi piiloutua sen taakse.

Minkään edellä mainitun puolesta: semanttinen toimintahäiriö.
Minkään edellä mainitun puolesta: dialoginen hyväntekeväisyys.

Oikea vastaus

Mikä sai minut kirjoittamaan tämän kirjoituksen? Lukemattomien peruskoululaisten tavoin viisivuotiaat kaksospoikani – alussa mainitut peruskoululaiset – saivat hiljattain kotitehtävässään tämän kysymyksen. Toinen valitsi vaihtoehdon ”1” ja toinen ”0”, ja olen yrittänyt kuvata ja laajentaa heidän perusteluitaan edellä. Molemmat vastaukset ovat mielestäni täysin puolustettavissa – eikä kumpikaan ole lopullisesti oikea.

Mitä sinun pitäisi siis tehdä, jos sinulta kysytään kysymys: Kuinka monta sivua ympyrällä on? Mielestäni optimaalinen vastaus on lähestyä elämäsi matemaatikkoa kirjoittamaan aiheesta 3000 sanan mittainen tutkielma, jonka voit sitten tulostaa ja toimittaa voitonriemuisesti epäonniselle opettajallesi. Mutta jos se ei onnistu, paras tapa on seurata Sokrateen esimerkkiä ja vastata kysymykseen vastakysymyksellä:

Kun kaikki on sanottu ja tehty, nollaan tai yhteen laskeminen tai kysymykseen vastaamisesta kieltäytyminen ei kerro meille käytännössä mitään ympyrän geometriasta. Mutta on paljon voitettavaa, kun irrotellaan tuttuja käsitteitä toisistaan, jätetään pois tai lisätään lisäehtoja, haastetaan intuitiomme siirtymällä yhdestä asiayhteydestä hieman erilaiseen ja yritetään kirjoittaa tarkasti, mitä tarkoitamme tietyllä termillä tietyssä ympäristössä. Siitä oikeassa matematiikassa on kyse.

Footnotes

Voisit tehdä jotain muuta: esim. valita ympyrästä lähtöpisteen P, josta mitataan etäisyys kehän ympäri. Julistetaan sitten, että rationaalisen etäisyyden päässä P olevat pisteet ovat kulmia ja loput sivuja. Näin saadaan laskennallisesti ääretön määrä kulmia ja laskennallisesti ääretön määrä sivuja. Voidaan myös määrätä päinvastoin. Tämä saattaisi sopia kätevästi monikulmioiden raja-arvoihin perustuvaan lähestymistapaan ympyröille, mutta minun on vaikea olla samaa mieltä siitä, että se on tarpeeksi helppoa tai ilmeistä, jotta sitä voitaisiin pitää ”oikeana vastauksena”.

Eräs Twitter-kirjeenvaihtajani oli huolissaan siitä, kuinka sileä käyrä on. Tämä hautakivi on jatkuvasti differentioituva, mutta ei kahdesti differentioituva. Olisi varmasti mielenkiintoista, jos monien mielestä tämä olisi kriittinen asia, ja tätä voisi varmaan testata jostain tällaisesta rakennetulla äärettömän sileällä hautakivellä, vaikken olekaan miettinyt yksityiskohtia.

Voisimme yrittää formalisoida tämän seuraavasti: Neliössä (tai missä tahansa monikulmiossa) sivulla on se ominaisuus, että mistä tahansa sisäkkäisestä kohdasta alkaen voit leikata muodon suoraan sijaintisi läpi niin, että valitsemasi sivu on tukevasti leikatun sivun toisella puolella. Tämä ei toimi kaksipuolisen hautakiven kohdalla: mikä tahansa leikkaus katkaisee aina pitkän sivun. Voisimme heikentää tätä sanomalla, että jotta sivu voidaan laskea sivuksi, on oltava ainakin yksi tapa leikata muodon läpi niin, että sivu on leikkauksen toisella puolella. Näin voisimme sanoa, että hautakivellä on neljä sivua (vaikka kaareva leikkaus ei olisikaan ylemmän alueen pisteiden toisella puolella). Ympyrän osalta sen oletettu yksi sivu ei kuitenkaan koskaan ole yhdellä sivulla (joten se suljettaisiin pois), ja vain puoliympyrän suora osa laskettaisiin sivuksi.

Ei ole helppoa keksiä tiukkaa perustelua, joka toimisi molemmille hautakiville, mutta ajattelen epävirallisemmin Schelling-pisteitä: eli paikkoja, jotka erottuvat erityisinä syistä, joita ei välttämättä ole helppo ennustaa etukäteen.

Kiitokset

Kiitos kaikille, jotka osallistuivat kyselyihini tai uudelleentwiittasivat niitä tai keskustelivat kanssani Twitterissä.