GeeksforGeeks

Edellytys – Graafiteorian perusteet – Sarja 1
Graafi on objektien joukko, jossa jotkin objektiparit ovat jossakin mielessä ”sukua” toisilleen. Graafin objektit vastaavat kärkipisteitä ja niiden väliset suhteet vastaavat reunoja. Graafi kuvataan kaavamaisesti kärkipisteitä kuvaavina pisteinä, joita yhdistävät särmiä kuvaavat viivat tai käyrät.
Formallisesti,

”Graafi koostuu , ei-tyhjästä kärkipisteiden (tai solmujen) joukosta ja , särmien joukosta. Jokaiseen reunaan liittyy joko yksi tai kaksi kärkeä, joita kutsutaan sen päätepisteiksi.”

Graafityypit :On olemassa useita graafityyppejä, jotka erotetaan toisistaan reunojen, niiden suunnan, painon jne. perusteella.

1. Yksinkertainen graafi – Graafia, jossa jokainen reuna yhdistää kaksi eri kärkeä ja jossa yksikään reuna ei yhdistä samaa kärkiparia, kutsutaan yksinkertaiseksi graafiksi. Tarkastellaan esimerkiksi seuraavaa kuvaajaa –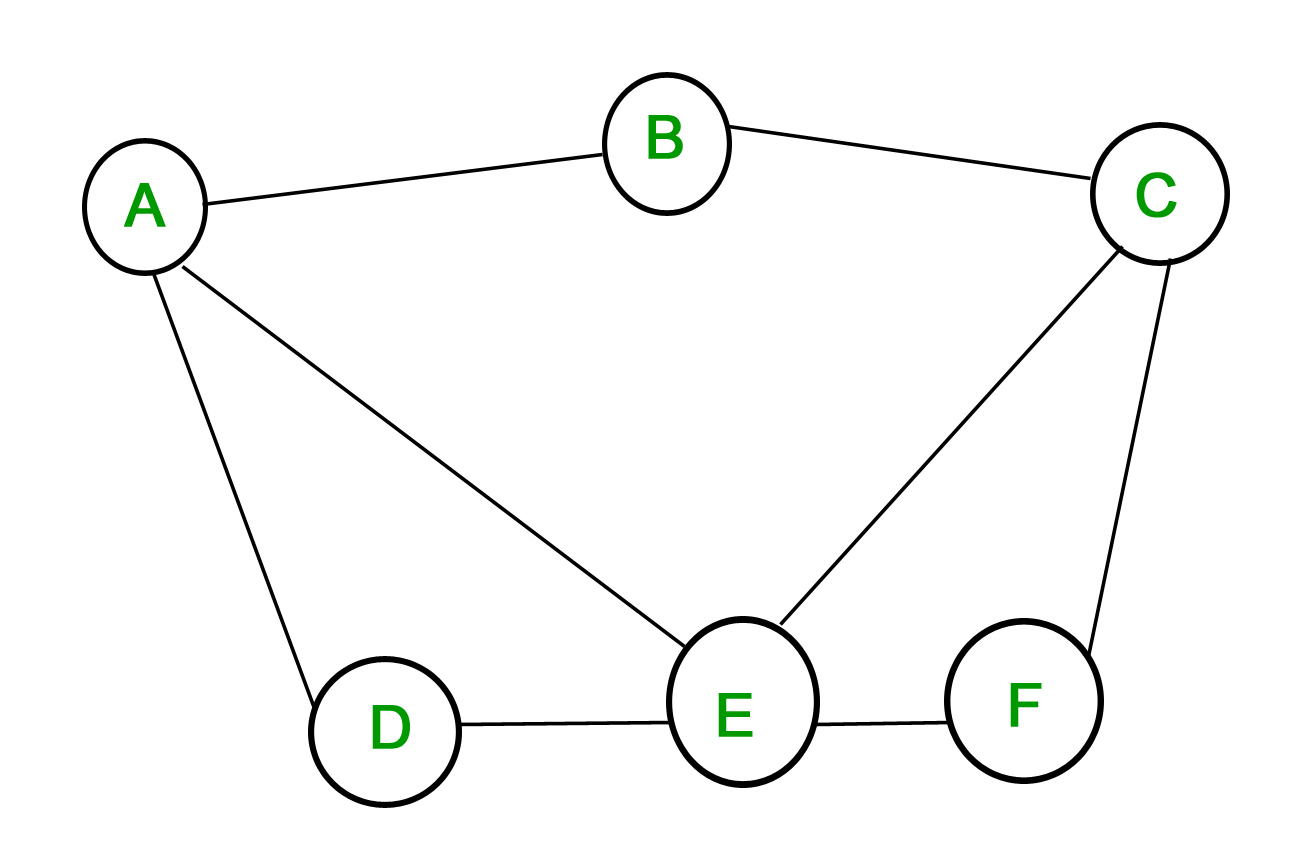

Yllä oleva kuvaaja on yksinkertainen kuvaaja, koska yhdelläkään kärkipisteellä ei ole itsesilmukkaa eikä kahta kärkeä yhdistä useampi kuin yksi särmä.
Särmiä merkitään niiden yhdistämillä kärkipisteillä- on särmä, joka yhdistää kärkipisteet ja .

2. Multigraafi – Graafia, jossa useat reunat voivat yhdistää saman kärkiparin, kutsutaan multigraafiksi.
Koska saman kärkiparin välillä voi olla useita reunoja, reunan moninaisuus kertoo kahden kärkipisteen välisten reunojen lukumäärän.

Ylläoleva graafi on multigraafi, koska :n ja :n välillä on useita reunoja. Reunan moninaisuus on 2.

Joissain graafeissa, toisin kuin edellä esitetyssä, reunat ovat suunnattuja. Tämä tarkoittaa, että kohteiden välinen suhde on vain yksisuuntainen eikä kaksisuuntainen. Joissakin sovelluksissa reunojen suunnalla voi olla merkitystä.

Se perusteella, ovatko reunat suunnattuja vai eivät, meillä voi olla suunnattuja ja suuntaamattomia graafeja. Tätä ominaisuutta voidaan laajentaa yksinkertaisiin graafeihin ja monigraafeihin, jolloin saadaan yksinkertaisia suunnattuja tai suuntaamattomia yksinkertaisia graafeja ja suunnattuja tai suuntaamattomia monigraafeja.

Basic graph Terminology :

Yllä olevassa keskustelussa on jo selitetty joitakin graafeihin liittyviä termejä, kuten kärkipisteet, reunat, suunnatut ja suuntaamattomat reunat jne. On muitakin termejä, jotka kuvaavat kärkipisteiden ja särmien ominaisuuksia.

• Vierekkäisyys – Graafissa kahden kärkipisteen ja sanotaan olevan vierekkäisiä, jos ne ovat reunan päätepisteitä. Reunan sanotaan osuvan kärkipisteisiin.
  Jos reuna on suunnattu, sanotaan olevan vierekkäin kanssa ja sanotaan olevan vierekkäin kanssa. Tällöin :n sanotaan olevan alkupiste ja :n sanotaan olevan loppupiste.
• aste – Pisteen aste on sen kanssa osuvien särmien lukumäärä, lukuun ottamatta itsesilmukkaa, joka vaikuttaa kaksi kertaa pisteen asteeseen. Vertexin astetta merkitään .
  Suuntautuneissa graafeissa aste luokitellaan edelleen in- ja out-asteiksi. Vertexin in-aste on niiden reunojen lukumäärä, joiden päätepisteenä on kyseinen vertex. Vertexin out-aste on niiden reunojen lukumäärä, joiden alkupisteenä on kyseinen vertex. In-aste merkitään :llä ja out-aste merkitään :lla.
  Esimerkiksi yllä olevassa suunnatussa graafissa, joka kuvaa kaupunkien välisiä lentoja, vertexin ”Delhi” in-aste on 3 ja sen out-aste on myös 3.

Huomautus: Jos vertexillä on nolla astetta, sitä kutsutaan eristetyksi. Jos aste on yksi, niin sitä sanotaan riippuvaksi.

Kädenvärinäteoreema :

Mitä saadaan, jos graafin kaikkien kärkien asteet lasketaan yhteen. Suuntaamattoman graafin tapauksessa jokainen särmä vaikuttaa kahdesti, kerran sen alkupisteen ja toisen kerran sen päätepisteen osalta. Asteiden summa on siis kaksinkertainen särmien lukumäärään nähden. Tämä tosiasia on todettu Handshaking-teoreemassa.

Let  be an undirected graph with  edges. ThenIn case G is a directed graph,

Handshaking-teoreemassa on suuntaamattomille graafeille mielenkiintoinen tulos –

An undirected graph has an even number of vertices of odd degree.

Todistus : Olkoon ja parillisen ja parittoman asteen kärkien joukot.
Tiedämme kädenpuristuslauseen avulla,

siten,

parillisen asteen kärkien asteiden summa on parillinen. LHS on myös parillinen, mikä tarkoittaa, että parittoman asteen omaavien kärkipisteiden asteiden summan täytyy olla parillinen.
Siten parittoman asteen omaavien kärkipisteiden lukumäärä on parillinen.

Joitakin erityisiä yksinkertaisia kuvaajia :

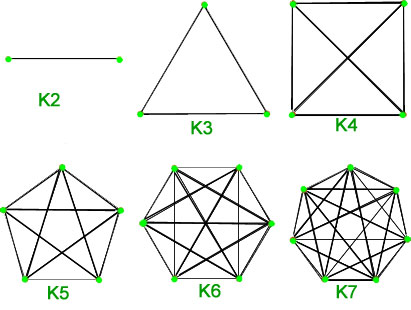
1. Täydelliset kuvaajat – kärkipisteiden yksinkertaista kuvaajaa, jolla on täsmälleen yksi särmä jokaisen kärkiparin välillä, kutsutaan täydelliseksi kuvaajaksi. Täydellistä graafia, jossa on kärkeä, merkitään . Särmien kokonaismäärä on n*(n-1)/2, kun täydellisessä graafissa on n kärkeä.

2. Syklit – Syklit ovat yksinkertaisia graafeja, joiden kärkipisteet ovat ja särmät . Sykli, jossa on kärkeä, merkitään . Reunojen kokonaismäärä on n, kun syklin graafissa on n kärkeä.

3. Pyörät – Pyörä on aivan kuten sykli, mutta siinä on yksi ylimääräinen huippu, joka on yhteydessä jokaiseen toiseen huippuun. Pyörät, joissa on kärkipistettä ja 1 lisäpiste, merkitään . Särmien kokonaismäärä on 2*(n-1), kun pyörän graafissa on n kärkeä.

4. Hyperkuutio – Hyperkuutio tai n-kuutio on graafi, jossa on kärkeä, joita kutakin edustaa n-bittinen merkkijono. Huiput, jotka eroavat toisistaan korkeintaan 1 bitin verran, ovat yhteydessä toisiinsa reunoilla. Hyperkuutio, jossa on kärkeä, on . Särmien kokonaismäärä on n*, kun kuution graafissa on kärkeä.

5. Kaksijakoiset graafit – Yksinkertaisen graafin sanotaan olevan kaksijakoinen, jos sen huippujoukko voidaan jakaa kahteen disjointiseen joukkoon siten, että jokaisen särmän alkupiste on ensimmäisessä joukossa ja loppupiste toisessa joukossa. Reunojen kokonaismäärä on (n*m), joilla on (n+m) kärkeä kaksijakoisessa graafissa.

Teoreema – Yksinkertainen graafi on kaksijakoinen, jos ja vain jos jokaiselle graafin kärkipisteelle voidaan antaa yksi kahdesta
eri väristä siten, että yhdellekään kahdelle vierekkäiselle kärkipisteelle ei anneta
samaa väriä.

Kaksinapaisen graafin, jonka kahdessa erillisessä osajoukossa on ja kärkeä, sanotaan olevan täydellinen, jos jokaisesta ensimmäisen joukon kärkipisteestä on särmä jokaiseen toisen joukon kärkipisteeseen, eli yhteensä särmää. Täydellistä kaksiosaista graafia, jossa on kärkeä ensimmäisessä joukossa ja kärkeä toisessa joukossa, merkitään .

GATE CS Corner Questions

Harjoittelemalla seuraavia kysymyksiä voit testata tietosi. Kaikki kysymykset on kysytty GATEssa aiempina vuosina tai GATEn koekokeissa. On erittäin suositeltavaa, että harjoittelet niitä.

1. GATE CS 2013, kysymys 25
2. GATE CS 2014 Set-1, kysymys 61
3. GATE CS 2006, kysymys 71
4. GATE CS 2002, kysymys 25
5. GATE CS 2004, kysymys 37
6. GATE CS 2014 Set-2, kysymys 13

Viitteet-

Graphs – Wikipedia
Discrete Mathematics and its Applications, kirjoittanut Kenneth H Rosen

Tämän artikkelin on kirjoittanut Chirag Manwani. Jos pidät GeeksforGeeksistä ja haluat osallistua, voit myös kirjoittaa artikkelin osoitteessa contribute.geeksforgeeks.org tai lähettää artikkelisi sähköpostitse osoitteeseen [email protected]. Näet artikkelisi näkyvän GeeksforGeeksin pääsivulla ja autat muita geekkejä.