- Resultados de aprendizaje
- Crecimiento lineal (algebraico)
- Predicción del crecimiento
- Crecimiento lineal
- Forma recursiva
- Forma explícita
- Conexión con el aprendizaje previo: Pendiente e Intercepción
- Ejemplos
- Forma recursiva
- Forma explícita
- Forma recursiva
- Forma explícita
- Pruébalo
- Cuando los buenos modelos se estropean
- Ejemplo
- Forma recursiva
- Forma explícita
- Crecimiento exponencial (geométrico )
- Crecimiento de la población
- Crecimiento exponencial
- Forma recursiva
- Forma explícita
- Ejemplo
- Evaluación de exponentes en la calculadora
- Inténtalo
- Ejemplos
- Redondeando
- Evaluación de raíces en la calculadora
- Pruébalo
- Ejemplo
Resultados de aprendizaje
- Determinar si los datos o un escenario describen un crecimiento lineal o geométrico
- Identificar tasas de crecimiento, valores iniciales o valores puntuales expresados verbalmente, gráficamente o numéricamente, y traducirlos a un formato utilizable en el cálculo
- Calcular ecuaciones recursivas y explícitas para el crecimiento lineal y geométrico dada la información suficiente, y utilizar esas ecuaciones para hacer predicciones
Tener una tasa de cambio constante es la característica que define el crecimiento lineal. El trazado de pares de coordenadas asociados a un cambio constante dará como resultado una línea recta, la forma del crecimiento lineal. En esta sección, formalizaremos una forma de describir el crecimiento lineal utilizando términos y conceptos matemáticos. Al final de esta sección, usted será capaz de escribir ecuaciones recursivas y explícitas para el crecimiento lineal dadas las condiciones iniciales, o una constante de cambio. También podrá reconocer la diferencia entre el crecimiento lineal y el geométrico dado un gráfico o una ecuación.

Crecimiento lineal (algebraico)
Predicción del crecimiento
Marco es un coleccionista de botellas de refresco antiguas. Su colección contiene actualmente 437 botellas. Cada año, presupuesta suficiente dinero para comprar 32 botellas nuevas. ¿Podemos determinar cuántas botellas tendrá dentro de 5 años, y cuánto tiempo tardará su colección en llegar a las 1000 botellas?

Aunque probablemente podrías resolver ambas preguntas sin una ecuación o matemática formal, vamos a formalizar nuestro enfoque de este problema para proporcionar un medio de responder a preguntas más complicadas.
Supongamos que Pn representa el número, o población, de botellas que tiene Marco después de n años. Así, P0 representaría el número de botellas ahora, P1 representaría el número de botellas después de 1 año, P2 representaría el número de botellas después de 2 años, y así sucesivamente. Podríamos describir cómo cambia la colección de botellas de Marco utilizando:
P0 = 437
Pn = Pn-1 + 32
Esto se llama una relación recursiva. Una relación recursiva es una fórmula que relaciona el siguiente valor de una secuencia con los valores anteriores. En este caso, el número de botellas del año n se puede encontrar sumando 32 al número de botellas del año anterior, Pn-1. Utilizando esta relación, podríamos calcular:
P1 = P0 + 32 = 437 + 32 = 469
P2 = P1 + 32 = 469 + 32 = 501
P3 = P2 + 32 = 501 + 32 = 533
P4 = P3 + 32 = 533 + 32 = 565
P5 = P4 + 32 = 565 + 32 = 597
Hemos respondido a la pregunta de cuántas botellas tendrá Marco dentro de 5 años. 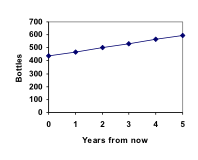
Sin embargo, resolver cuánto tardará su colección en llegar a 1000 botellas requeriría muchos más cálculos.
Aunque las relaciones recursivas son excelentes para describir de forma sencilla y limpia cómo cambia una cantidad, no son convenientes para hacer predicciones o resolver problemas que se extienden mucho en el futuro. Para ello, es preferible una forma cerrada o explícita de la relación. Una ecuación explícita nos permite calcular Pn directamente, sin necesidad de conocer Pn-1. Aunque es posible que ya puedas adivinar la ecuación explícita, vamos a derivarla a partir de la fórmula recursiva. Podemos hacerlo no simplificando selectivamente a medida que avanzamos:
P1 = 437 + 32 = 437 + 1(32)
P2 = P1 + 32 = 437 + 32 + 32 = 437 + 2(32)
P3 = P2 + 32 = (437 + 2(32)) + 32 = 437 + 3(32)
P4 = P3 + 32 = (437 + 3(32)) + 32 = 437 + 4(32)
Probablemente ahora puedas ver el patrón, y generalizar que
Pn = 437 + n(32) = 437 + 32n
Usando esta ecuación, podemos calcular cuántas botellas tendrá después de 5 años:
P5 = 437 + 32(5) = 437 + 160 = 597
Ahora también podemos resolver cuándo la colección llegará a 1000 botellas sustituyendo Pn por 1000 y resolviendo n
1000 = 437 + 32n
563 = 32n
n = 563/32 = 17.59
Por tanto, Marco llegará a las 1000 botellas en 18 años.
Los pasos para determinar la fórmula y resolver el problema de la colección de botellas de Marco se explican con detalle en los siguientes vídeos.
En este ejemplo, la colección de Marco creció en el mismo número de botellas cada año. Este cambio constante es la característica que define el crecimiento lineal. Trazando los valores que hemos calculado para la colección de Marco, podemos ver que los valores forman una línea recta, la forma del crecimiento lineal.
Crecimiento lineal
Si una cantidad comienza en el tamaño P0 y crece en d cada periodo de tiempo, entonces la cantidad después de n periodos de tiempo se puede determinar utilizando cualquiera de estas relaciones:
Forma recursiva
Pn = Pn-1 + d
Forma explícita
Pn = P0 + d n
En esta ecuación, d representa la diferencia común: la cantidad que cambia la población cada vez que n aumenta en 1.
Conexión con el aprendizaje previo: Pendiente e Intercepción
Puede reconocer la diferencia común, d, en nuestra ecuación lineal como pendiente. De hecho, toda la ecuación explícita debe parecerte familiar – es la misma ecuación lineal que aprendiste en álgebra, probablemente enunciada como y = mx + b.
En la ecuación algebraica estándar y = mx + b, b era la intersección y, o el valor de y cuando x era cero. En la forma de la ecuación que estamos usando, estamos usando P0 para representar esa cantidad inicial.
En la ecuación y = mx + b, recuerda que m era la pendiente. Usted puede recordar esto como «aumento sobre la carrera», o el cambio en y dividido por el cambio en x. De cualquier manera, representa lo mismo que la diferencia común, d, que estamos utilizando – la cantidad que la salida Pn cambia cuando la entrada n aumenta en 1.
Las ecuaciones y = mx + b y Pn = P0 + d n significan lo mismo y se pueden utilizar de la misma manera. Sólo lo escribimos de forma algo diferente.
Ejemplos
La población de alces en un bosque nacional se midió en 12.000 en 2003, y se volvió a medir en 15.000 en 2007. Si la población sigue creciendo linealmente a este ritmo, ¿cuál será la población de alces en 2014?
Vea más sobre este ejemplo aquí.
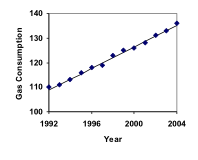
El consumo de gasolina en Estados Unidos ha ido aumentando de forma constante. Los datos de consumo de 1992 a 2004 se muestran a continuación. Encuentre un modelo para estos datos y utilícelo para predecir el consumo en 2016. Si la tendencia continúa, ¿cuándo alcanzará el consumo los 200.000 millones de galones?
| Año | ’92 | ’93 | ’94 | ’95 | ’96 | ’97 | ’98 | ’99 | ’00 | ’01 | ’02 | ’03 | ’04 |
| Consumo (mil millones de galones) | 110 | 111 | 113 | 116 | 118 | 119 | 123 | 125 | 126 | 128 | 131 | 133 | 136 |
Los pasos para llegar a esta respuesta se detallan en el siguiente vídeo.
El coste, en dólares, de una suscripción al gimnasio durante n meses puede describirse mediante la ecuación explícita Pn = 70 + 30n. ¿Qué nos dice esta ecuación?
La explicación de este ejemplo se detalla a continuación.
Pruébalo
El número de padres que se quedan en casa en Canadá ha ido creciendo de forma constante. Aunque la tendencia no es perfectamente lineal, sí lo es bastante. Usa los datos de 1976 y 2010 para encontrar una fórmula explícita para el número de padres que se quedan en casa, y luego úsala para predecir el número en 2020.
| Año | 1976 | 1984 | 1991 | 2000 | 2010 |
| Número de padres que se quedan en casa | 20610 | 28725 | 43530 | 47665 | 53555 |
Cuando los buenos modelos se estropean
Cuando se utilizan modelos matemáticos para predecir el comportamiento futuro, es importante tener en cuenta que muy pocas tendencias continuarán indefinidamente.
Ejemplo
Supongamos que un niño de cuatro años mide actualmente 39 pulgadas, y se le dice que debe crecer 2,5 pulgadas al año.
Podemos establecer un modelo de crecimiento, con n = 0 correspondiente a los 4 años.
Forma recursiva
P0 = 39
Pn = Pn-1 + 2,5
Forma explícita
Pn = 39 + 2.5(n)
Así que a los 6 años, esperaríamos que midiera
P2 = 39 + 2,5(2) = 44 pulgadas
Cualquier modelo matemático se romperá eventualmente. Ciertamente, no debemos esperar que este chico siga creciendo al mismo ritmo toda su vida. Si lo hiciera, a los 50 años mediría
P46 = 39 + 2,5(46) = 154 pulgadas de altura = ¡12,8 pies!
Cuando usamos cualquier modelo matemático, tenemos que considerar qué entradas son razonables. Siempre que extrapolamos, o hacemos predicciones en el futuro, estamos asumiendo que el modelo seguirá siendo válido.
Vea una explicación en vídeo de este desglose del modelo de crecimiento lineal aquí.
Crecimiento exponencial (geométrico )
Crecimiento de la población
Suponga que cada año, sólo el 10% de los peces de un lago tienen crías supervivientes. Si el año pasado había 100 peces en el lago, ahora habría 110 peces. Si el año pasado había 1000 peces en el lago, ahora habría 1100 peces. En ausencia de factores inhibidores, las poblaciones de personas y animales tienden a crecer en un porcentaje de la población existente cada año.

Supongamos que nuestro lago comenzó con 1000 peces, y que el 10% de los peces tienen descendencia superviviente cada año. Como empezamos con 1000 peces, P0 = 1000. ¿Cómo calculamos P1? La nueva población será la antigua, más un 10% adicional. Simbólicamente:
P1 = P0 + 0,10P0
Nótese que esto podría condensarse en una forma más breve mediante la factorización:
P1 = P0 + 0,10P0 = 1P0 + 0,10P0 = (1+ 0,10)P0 = 1,10P0
Mientras que el 10% es la tasa de crecimiento, 1,10 es el multiplicador de crecimiento. Obsérvese que 1,10 puede considerarse como «el 100% original más un 10% adicional»
Para nuestra población de peces,
P1 = 1,10(1000) = 1100
Podemos entonces calcular la población en años posteriores:
P2 = 1,10P1 = 1,10(1100) = 1210
P3 = 1,10P2 = 1,10(1210) = 1331
Nota que en el primer año, la población creció en 100 peces; en el segundo, en 110; y en el tercero, en 121.
Aunque hay un crecimiento porcentual constante, el aumento real del número de peces aumenta cada año.
Graficando estos valores vemos que este crecimiento no parece del todo lineal.
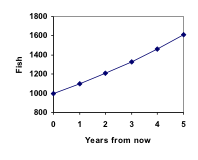
Un recorrido por este escenario de peces puede verse aquí:
Para tener una mejor idea de cómo afecta este crecimiento porcentual, necesitamos una forma explícita, para poder calcular rápidamente los valores más allá en el futuro.
Al igual que hicimos con el modelo lineal, empezaremos a construir a partir de la ecuación recursiva:
P1 = 1,10(P0 )= 1,10(1000)
P2 = 1,10(P1 )= 1,10(1,10(1000)) = 1,102(1000)
P3 = 1.10(P2 )= 1.10(1.102(1000)) = 1.103(1000)
P4 = 1.10(P3 )= 1.10(1.103(1000)) = 1.104(1000)
Observando un patrón, podemos generalizar la forma explícita para que sea:
Pn = 1.10n(1000), o, equivalentemente, Pn = 1000(1,10n)
A partir de esto, podemos calcular rápidamente el número de peces en 10, 20 o 30 años:
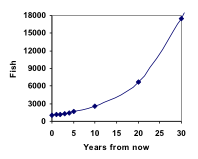
P10 = 1.1010(1000) = 2594
P20 = 1.1020(1000) = 6727
P30 = 1.1030(1000) = 17449
Agregando estos valores a nuestra gráfica se observa una forma que definitivamente no es lineal. Si nuestra población de peces hubiera crecido linealmente, a razón de 100 peces cada año, la población sólo habría alcanzado los 4000 en 30 años, en comparación con los casi 18.000 con este crecimiento basado en porcentajes, llamado crecimiento exponencial.
Un vídeo que demuestra el modelo explícito de esta historia de peces puede verse aquí:
En el crecimiento exponencial, la población crece de forma proporcional al tamaño de la población, por lo que a medida que la población aumenta, el mismo crecimiento porcentual producirá un crecimiento numérico mayor.
Crecimiento exponencial
Si una cantidad comienza en el tamaño P0 y crece en un R% (escrito como un decimal, r) cada período de tiempo, entonces la cantidad después de n períodos de tiempo se puede determinar utilizando cualquiera de estas relaciones:
Forma recursiva
Pn = (1+r) Pn-1
Forma explícita
Pn = (1+r)n P0 o, equivalentemente, Pn = P0 (1+r)n
Llamamos r a la tasa de crecimiento.
El término (1+r) se llama multiplicador de crecimiento, o ratio común.
Ejemplo
Entre 2007 y 2008, Olympia, WA creció casi un 3% hasta alcanzar una población de 245 mil personas. Si esta tasa de crecimiento continuara, ¿cuál sería la población de Olympia en 2014?
El siguiente vídeo explica este ejemplo en detalle.
Evaluación de exponentes en la calculadora
Para evaluar expresiones como (1,03)6, será más fácil utilizar una calculadora que multiplicar 1,03 por sí mismo seis veces. La mayoría de las calculadoras científicas tienen un botón para los exponentes. Normalmente está etiquetado como:
^ , yx , o xy .
Para evaluar 1,036 escribiríamos 1,03 ^ 6, o 1,03 yx 6. Pruébalo – deberías obtener una respuesta en torno a 1,1940523.
Inténtalo
La India es el segundo país más poblado del mundo, con una población en 2008 de unos 1.140 millones de personas. La población crece aproximadamente un 1,34% cada año. Si esta tendencia continúa, ¿cuál será la población de la India en 2020?
Ejemplos
Una amiga está utilizando la ecuación Pn = 4600(1.072)n para predecir la matrícula anual en una universidad local. Dice que la fórmula se basa en los años posteriores a 2010. ¿Qué nos dice esta ecuación?
Vea lo siguiente para ver este ejemplo elaborado.
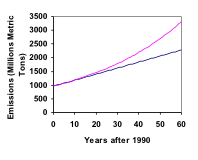
En 1990, el uso de energía residencial en los Estados Unidos era responsable de 962 millones de toneladas métricas de emisiones de dióxido de carbono. En el año 2000, esa cifra había aumentado a 1182 millones de toneladas métricas. Si las emisiones crecen exponencialmente y continúan al mismo ritmo, ¿a cuánto ascenderán las emisiones en 2050?
Vea más sobre este ejemplo aquí.
Redondeando
Como nota sobre el redondeo, observe que si hubiéramos redondeado la tasa de crecimiento al 2,1%, nuestro cálculo para las emisiones en 2050 habría sido 3347. El redondeo al 2% habría cambiado nuestro resultado a 3156. Una diferencia muy pequeña en las tasas de crecimiento se magnifica enormemente en el crecimiento exponencial. Por esta razón, se recomienda redondear la tasa de crecimiento lo menos posible.
Si necesita redondear, mantenga al menos tres dígitos significativos – números después de cualquier cero inicial. Así, 0,4162 podría redondearse razonablemente a 0,416. Una tasa de crecimiento de 0,001027 podría redondearse razonablemente a 0,00103.
Evaluación de raíces en la calculadora
En el ejemplo anterior, tuvimos que calcular la raíz 10 de un número. Esto es diferente a sacar la raíz cuadrada básica, √. Muchas calculadoras científicas tienen un botón para las raíces generales. Suele estar etiquetado como:
\aqrt{x}
Para evaluar la raíz 3 de 8, por ejemplo, escribiríamos 3 \aqrt{} 8, o 8 \qrt{}} 3, dependiendo de la calculadora. Pruébalo en la tuya para ver cuál usar – deberías obtener una respuesta de 2.
Si tu calculadora no tiene un botón de raíz general, no está todo perdido. En su lugar, puedes utilizar la propiedad de los exponentes, que establece que:
cuadrado{a}={a}^{frac{1}{2}}.
Así que, para calcular la tercera raíz de 8, podrías utilizar la tecla de exponentes de tu calculadora para evaluar 81/3. Para ello, escribe:
8 yx ( 1 ÷ 3 )
Los paréntesis indican a la calculadora que debe dividir 1/3 antes de hacer el exponente.
Pruébalo
El número de usuarios de una red social era de 45 mil en febrero, cuando se hizo pública oficialmente, y aumentó a 60 mil en octubre. Si el sitio está creciendo exponencialmente, y el crecimiento continúa al mismo ritmo, ¿cuántos usuarios deben esperar dos años después de que salieron a bolsa?
Ejemplo
Volviendo al último ejemplo, para comparar, ¿cuáles serían las emisiones de carbono en 2050 si las emisiones crecen linealmente al mismo ritmo?
Una demostración de este ejemplo puede verse en el siguiente video.
Entonces, ¿cómo sabemos qué modelo de crecimiento usar cuando trabajamos con datos? Hay dos enfoques que deben utilizarse juntos siempre que sea posible:
- Encuentra más de dos datos. Grafique los valores y busque una tendencia. ¿Parece que los datos cambian como una línea, o que los valores se curvan hacia arriba?
- Considere los factores que contribuyen a los datos. ¿Son cosas que se espera que cambien de forma lineal o exponencial? Por ejemplo, en el caso de las emisiones de carbono, podríamos esperar que, en ausencia de otros factores, estuvieran estrechamente ligadas a los valores de la población, que tienden a cambiar exponencialmente.