Indledning
I datalogi er en rettet acyklisk graf (DAG) en rettet graf uden cyklusser. I denne vejledning viser vi, hvordan man laver en topologisk sortering på en DAG i lineær tid.
Topologisk sortering
I mange applikationer bruger vi dirigerede acykliske grafer til at angive præcedenser mellem begivenheder. I et planlægningsproblem er der f.eks. et sæt opgaver og et sæt begrænsninger, der angiver rækkefølgen af disse opgaver. Vi kan konstruere en DAG til at repræsentere opgaver. De dirigerede kanter i DAG’en repræsenterer rækkefølgen af opgaverne.
Lad os overveje et problem med, hvordan en person kan klæde sig på til en formel lejlighed. Vi skal tage flere beklædningsgenstande på, f.eks. sokker, bukser, sko osv. Nogle beklædningsgenstande skal tages på før de andre. F.eks. skal vi tage sokker på før skoene. Nogle beklædningsgenstande kan tages på i vilkårlig rækkefølge, f.eks. sokker og bukser. Vi kan bruge en DAG til at illustrere dette problem:
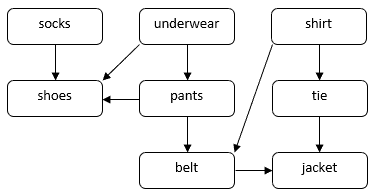
I denne DAG svarer toppene til beklædningsgenstande. En direkte kant 
i DAG’en angiver, at vi skal tage beklædningsgenstand 
på før beklædningsgenstand 
. Vores opgave er at finde en rækkefølge til at tage alle beklædningsgenstande på, samtidig med at afhængighedsbegrænsningerne overholdes. Vi kan f.eks. tage tøjet på i følgende rækkefølge:
En topologisk sortering af en DAG 
er en lineær rækkefølge af alle dens toppunkter, således at hvis indeholder en kant , så kommer før i rækkefølgen. For en DAG kan vi konstruere en topologisk sortering med en løbetid, der er lineær i forhold til antallet af hjørner plus antallet af kanter, hvilket er 
.
Kahns algoritme
I en DAG har enhver sti mellem to hjørner en endelig længde, da grafen ikke indeholder en cyklus. Lad 
være den længste sti fra (kildevertikal) til (destinationsvertikal). Da er den længste sti, kan der ikke være nogen indgående kant til . Derfor indeholder en DAG mindst ét toppunkt, som ikke har nogen indgående kant.
3.1. Kahns algoritme
I Kahns algoritme konstruerer vi en topologisk sortering på en DAG ved at finde toppunkter, der ikke har nogen indgående kanter:
I denne algoritme beregner vi først værdierne for in-dygtighed for alle toppunkter.
Dernæst starter vi med et toppunkt, hvis in-dygtighed er 0, og sætter det i slutningen af outputlisten. Når vi vælger et toppunkt, opdaterer vi in-degree-værdierne for dets tilstødende toppunkter, fordi toppunktet og dets udkanter fjernes fra grafen.
Vi kan gentage ovenstående proces, indtil vi har valgt alle toppunkter. Udgangslisten er så en topologisk sortering af grafen.
3.2. Tidskompleksitet
For at beregne in-degrees for alle toppene skal vi besøge alle toppene og kanter i . Derfor er løbetiden for in-degree-beregninger. For at undgå at beregne disse værdier igen kan vi bruge et array til at holde styr på in-degree-værdierne for disse hjørner. Inden for while-loop’en skal vi også besøge alle hjørner og kanter. Derfor er den samlede løbetid .
Depth First Search
Vi kan også bruge en DFS-algoritme (Depth First Search) til at konstruere den topologiske sortering.
4.1. Graf DFS med rekursion
Hvor vi tager fat på det topologiske sorteringsaspekt med DFS, skal vi starte med at gennemgå en standard, rekursiv DFS-traversal-algoritme for grafer:
I standard-DFS-algoritmen starter vi med et tilfældigt toppunkt i og markerer dette toppunkt som besøgt. Derefter kalder vi rekursivt dfsRecursive-funktionen for at besøge alle dets ikke besøgte tilstødende toppunkter. På denne måde kan vi besøge alle vertices i på tid.
Men da vi sætter hvert vertex ind i listen straks, når vi besøger det, og da vi kan starte ved et vilkårligt vertex, kan standard-DFS-algoritmen ikke garantere, at den genererer en topologisk sorteret liste.
Lad os se, hvad vi skal gøre for at afhjælpe denne mangel.
4.2. DFS-baseret topologisk sorteringsalgoritme
Vi kan modificere DFS-algoritmen til at generere en topologisk sortering af en DAG. Under DFS-traverseringen, efter at alle naboer til et toppunkt er besøgt, sætter vi det derefter forrest på resultatlisten 
. På denne måde kan vi sikre os, at optræder før alle sine naboer i den sorterede liste:
Denne algoritme svarer til den almindelige DFS-algoritme. Selv om vi stadig starter med et tilfældigt toppunkt, sætter vi ikke toppunktet ind i listen med det samme, når vi besøger det. I stedet besøger vi først alle dets naboer rekursivt og sætter derefter toppunktet forrest på listen. Hvis indeholder en kant , vises derfor før i listen.
Den samlede løbetid er også , da den har samme tidskompleksitet som DFS-algoritmen.
Slutning
I denne artikel har vi vist et eksempel på topologisk sortering på en DAG. Desuden diskuterede vi to algoritmer, der kan lave en topologisk sortering på tid.
Java-implementeringen af den DFS-baserede topologiske sorteringsalgoritme er tilgængelig i vores artikel om Depth First Search in Java.