Vend tilbage til lektionernes indeks | Gennemfør lektionerne i rækkefølge | Udskriv venlig side
Operationer i matrixrækker (side 1 af 2)
“Operationer” er matematiker-sprog for “procedurer”. De fire “grundlæggende operationer” på tal er addition, subtraktion, multiplikation og division. For matricer er der tre grundlæggende rækkeoperationer; det vil sige, at der er tre procedurer, som man kan udføre med rækkerne i en matrix.
Den første operation er række-skiftning. For eksempel, givet matricen:

…kan du bytte rundt på rækkerne for at sætte matricen i en pænere rækkearrangement, som her:
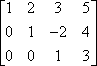
Række-skiftet angives ofte ved at tegne pile, som her:

Når du bytter rundt på rækkerne, skal du være omhyggelig med at kopiere posterne korrekt.
Den anden operation er række-multiplikation. For eksempel, givet følgende matrix:

…kan man gange den første række med -1 for at få en positiv ledende værdi i den første række:
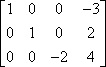
Denne rækkemultiplikation angives ofte ved hjælp af en pil med multiplikation anført ovenpå, som her:
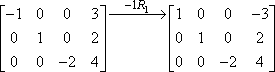
Den “-1R1” angiver den egentlige operation. “-1” siger, at vi har ganget med negativ et; “R1” siger, at vi arbejdede med den første række. Bemærk, at den anden og tredje række blev kopieret uændret ned i den anden matrix. Multiplikationen gjaldt kun for den første række, så posterne for de to andre rækker blev bare ført med uændret.
Du kan gange med hvad du vil. For f.eks. at få en ledende 1 i den tredje række i den foregående matrix kan du gange den tredje række med en negativ halvdel:

Da du ikke gjorde noget med den første og anden række, blev disse poster bare kopieret uændret over i den nye matrix.
Du kan foretage mere end én rækkemultiplikation inden for samme trin, så du kunne have foretaget de to ovenstående trin i ét trin, som her:
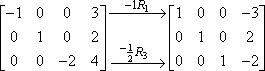
Det er en god idé at bruge en eller anden form for notation (som f.eks. pilene og subscripterne ovenfor), så du kan holde styr på dit arbejde. Matricer er meget rodet, især hvis du laver dem i hånden, og noter kan gøre det lettere at kontrollere dit arbejde senere. Det vil også imponere din lærer.
Den sidste rækkeoperation er rækkeaddition. Rækkeaddition svarer til “addition”-metoden til løsning af systemer af lineære ligninger. Antag, at du har følgende ligningssystem:
x + 3y = 1
-x + y = 3 Copyright © Elizabeth Stapel 2003-2011 All Rights Reserved
Advertering
Du kan begynde at løse dette system ved at addere nedad i kolonnerne for at få 4y = 4:
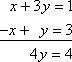
Du kan gøre noget lignende med matricer.Givet f.eks. følgende matrix:

… kan du “reducere” (få flere ledende nuller i) den anden række ved at lægge den første række til den (det generelle mål med matricer på dette stadium er at få en “1” – eller “0’er” og derefter en “1” – i begyndelsen af hver matrixrække). Da du reducerede det lineære system med to ligninger ved at lægge det sammen, tegnede du en “ligestreg” på tværs af bunden og lagde det sammen nedad. Når du bruger addition på en matrix, skal du have fat i noget skrabepapir, for du vil ikke forsøge at udføre arbejdet inde i matrixen. Så læg de to rækker sammen på dit skrabepapir:
|
Skrabearbejde – |
|
Dette er din nye anden række; du skriver den i stedet for den gamle anden række. Resultatet vil se således ud:
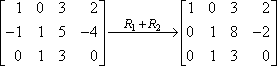
I dette tilfælde betyder “R1 + R2” på pilen: “Jeg tilføjede række et til række to, og dette er det resultat, jeg fik”. Da række et faktisk ikke ændrede sig, og da vi ikke gjorde noget ved række tre, bliver disse rækker kopieret uændret ind i den nye matrix.
Top | 1 | 2 | Retur til indeks Næste >>
|
Citer denne artikel som: |
Stapel, Elizabeth. “Matrix Row Operations”. Purplemath. Tilgængelig fra 2016
|