Klassifikation ved hjælp af diskriminantanalyse
Lad os se, hvordan LDA kan afledes som en overvåget klassifikationsmetode. Overvej et generisk klassifikationsproblem: En tilfældig variabel X kommer fra en af K klasser, med nogle klassespecifikke sandsynlighedsdensiteter f(x). En diskriminantregel forsøger at opdele datarummet i K disjunkte regioner, der repræsenterer alle klasser (forestil dig kasserne på et skakbræt). Med disse regioner betyder klassificering ved hjælp af diskriminantanalyse blot, at vi henfører x til klasse j, hvis x befinder sig i region j. Spørgsmålet er så, hvordan vi ved, hvilken region dataene x falder i? Vi kan naturligvis følge to tildelingsregler:
- Maximum likelihood-regel: Hvis vi antager, at hver klasse kan forekomme med samme sandsynlighed, så tildel x til klasse j, hvis
- Bayesian-regel: Hvis vi kender klassens prioritets sandsynligheder, π, skal x henføres til klasse j hvis

Linjær og kvadratisk diskriminantanalyse
Hvis vi antager, at data kommer fra en multivariat Gauss-fordeling, i.dvs. at fordelingen af X kan karakteriseres ved dens middelværdi (μ) og kovarians (Σ), kan man få eksplicitte former af ovenstående fordelingsregler. Efter den bayesianske regel klassificerer vi data x til klasse j, hvis den har den højeste sandsynlighed blandt alle K klasser for i = 1,…,K:

Den ovenstående funktion kaldes diskriminantfunktionen. Bemærk brugen af log-likelihood her. Med andre ord fortæller diskriminantfunktionen os, hvor sandsynligt det er, at data x er fra hver klasse. Beslutningsgrænsen, der adskiller to klasser, k og l, er derfor det sæt af x, hvor to diskriminantfunktioner har den samme værdi. Derfor er alle data, der falder på beslutningsgrænsen, lige sandsynlige fra de to klasser (vi kunne ikke bestemme os).
LDA opstår i det tilfælde, hvor vi antager lige stor kovarians mellem K klasser. Det vil sige, at i stedet for én kovariansmatrix pr. klasse, har alle klasser den samme kovariansmatrix. Så kan vi få følgende diskriminantfunktion:

Bemærk, at dette er en lineær funktion i x. Således er beslutningsgrænsen mellem ethvert par klasser også en lineær funktion i x, hvilket er årsagen til navnet: lineær diskriminantanalyse. Uden antagelsen om lige kovarians ophæves det kvadratiske udtryk i sandsynligheden ikke, og derfor er den resulterende diskriminantfunktion en kvadratisk funktion i x:

I dette tilfælde er beslutningsgrænsen kvadratisk i x. Dette er kendt som kvadratisk diskriminantanalyse (QDA).
Hvilken er bedst? LDA eller QDA?
I virkelige problemer er populationsparametrene normalt ukendte og estimeres ud fra træningsdata som stikprøvens middelværdier og stikprøvekovariansmatricer. QDA giver mulighed for mere fleksible beslutningsgrænser i forhold til LDA, men antallet af parametre, der skal estimeres, stiger også hurtigere end for LDA. For LDA er der behov for (p+1) parametre for at konstruere den diskriminante funktion i (2). For et problem med K klasser ville vi kun have brug for (K-1) sådanne diskriminantfunktioner ved vilkårligt at vælge én klasse som basisklasse (ved at trække basisklassens sandsynlighed fra alle andre klasser). Derfor er det samlede antal estimerede parametre for LDA (K-1)(p+1).
På den anden side skal der for hver QDA-diskriminantfunktion i (3) estimeres middelvektor, kovariansmatrix og klasseprioritet for hver QDA-diskriminantfunktion i (3):
– Middelværdi: p
– Kovarians: p(p+1)/2
– Klasseprioritet: 1
Sådan er det for QDA nødvendigt at estimere (K-1){p(p(p+3)/2+1} parametre.
Dermed stiger antallet af parametre, der estimeres i LDA, lineært med p, mens det for QDA stiger kvadratisk med p. Vi ville forvente, at QDA har dårligere præstationer end LDA, når problemdimensionen er stor.
Bedste af to verdener? Kompromis mellem LDA & QDA
Vi kan finde et kompromis mellem LDA og QDA ved at regulere de individuelle klassekovariansmatricer. Regularisering betyder, at vi lægger en vis begrænsning på de estimerede parametre. I dette tilfælde kræver vi, at den individuelle kovariansmatrix skrumper mod en fælles pulje-kovariansmatrix gennem en strafparameter, f.eks. α:

Den fælles kovariansmatrix kan også reguleres mod en identitetsmatrix gennem en strafparameter, f.eks, β:

I situationer, hvor antallet af inputvariabler i høj grad overstiger antallet af stikprøver, kan kovariansmatrixen være dårligt estimeret. Shrinkage kan forhåbentlig forbedre estimationen og klassifikationsnøjagtigheden. Dette illustreres af nedenstående figur.

Beregning for LDA
Vi kan se af (2) og (3), at beregninger af diskriminantfunktioner kan forenkles, hvis vi diagonaliserer kovariansmatricerne først. Det vil sige, at dataene transformeres til at have en identisk kovariansmatrix (ingen korrelation, varians på 1). I tilfælde af LDA er det således, hvordan vi går frem med beregningen:

Strin 2 kugler dataene for at producere en identitetskovariansmatrix i det transformerede rum. Trin 4 fås ved at følge (2).
Lad os tage et eksempel med to klasser for at se, hvad LDA virkelig gør. Antag, at der er to klasser, k og l. Vi klassificerer x til klasse k, hvis

Overstående betingelse betyder, at det er mere sandsynligt, at klasse k producerer data x end klasse l. Efter de fire trin, der er skitseret ovenfor, skriver vi
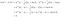
Det vil sige, vi klassificerer data x til klasse k, hvis

Den afledte tildelingsregel afslører, hvordan LDA fungerer. Ligningens venstre side (l.h.s.) er længden af den ortogonale projektion af x* på det linjestykke, der forbinder de to klassemidler. Højre side er placeringen af centrum af segmentet korrigeret med klassens prioritets-sandsynligheder. LDA klassificerer i det væsentlige de sphered data til den nærmeste klassemiddelværdi. Vi kan gøre to iagttagelser her:
- Der er tale om, at beslutningspunktet afviger fra midtpunktet, når klassens prior-sandsynligheder ikke er de samme, dvs. at grænsen skubbes mod klassen med en mindre prior-sandsynlighed.
- Data projiceres på det rum, der er opspændt af klassens middelværdier (multiplikation af x* og middelværdi-subtraktion på l.h.s. af reglen). Afstandssammenligninger foretages derefter i dette rum.