- Sammenhæng er et grundlæggende begreb i grafteori. Det definerer, om en graf er forbundet eller frakoblet. Uden konnektivitet er det ikke muligt at krydse en graf fra et toppunkt til et andet toppunkt.
- En graf siges at være en sammenhængende graf, hvis der er en sti mellem hvert par toppunkt. Fra hvert toppunkt til ethvert andet toppunkt skal der være en sti, der kan gennemløbes. Dette kaldes en grafs konnektivitet.
- En graf siges at være usammenhængende, hvis der findes flere usammenhængende hjørner og kanter.
- Graph connectivity theories are essential in network applications, routing transportation networks, network tolerance etc.
Example
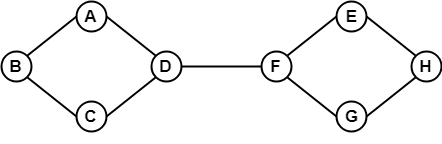
I ovenstående eksempel er det muligt at rejse fra et hjørne til et andet hjørne. Her kan vi rejse fra toppunkt B til H ved hjælp af stien B -> A -> D -> F -> E -> H. Derfor er det en sammenhængende graf.
Eksempel
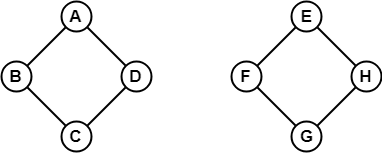
I ovenstående eksempel er det ikke muligt at rejse fra toppunkt B til H, fordi der ikke er nogen sti mellem dem direkte eller indirekte. Derfor er det en usammenhængende graf.
Lad os se nogle grundlæggende koncepter for konnektivitet.
Snitpunkt
Et enkelt punkt, hvis fjernelse afbryder forbindelsen i en graf, kaldes et snitpunkt.
Lad G være en sammenhængende graf. Et toppunkt v i G kaldes et afskåret toppunkt i G, hvis G-v (Fjern v fra G) resulterer i en usammenhængende graf.
Når vi fjerner et toppunkt fra en graf, vil grafen blive opdelt i to eller flere grafer. Dette toppunkt kaldes et afskåret toppunkt.
Note: Lad G være en graf med n toppunkter:
- En sammenhængende graf G kan højst have (n-2) afskårne toppunkter.
- Fjernelse af et afskåret toppunkt kan efterlade en graf usammenhængende.
- Fjernelse af et toppunkt kan øge antallet af komponenter i en graf med mindst én.
- Alle ikke-vedhængende toppunkt i et træ er et afskåret toppunkt.
Eksempel 1

Eksempel 2
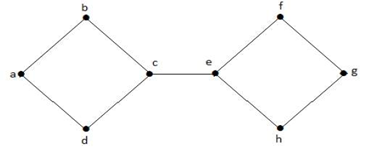
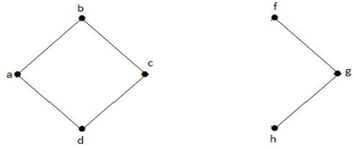
I ovenstående graf er toppunktet “e” et afskåret toppunkt. Efter fjernelse af toppunktet ‘e’ fra ovenstående graf vil grafen blive en usammenhængende graf.
Cut Edge (Bridge)
En cut- Edge eller bridge er en enkelt kant, hvis fjernelse afbryder forbindelsen mellem en graf.
Lad G være en sammenhængende graf. En kant e i G kaldes en afskåret kant i G, hvis G-e (Fjern e fra G) resulterer i en frakoblet graf.
Når vi fjerner en kant fra en graf, vil grafen blive opdelt i to eller flere grafer. Denne fjernelseskant kaldes en afskåret kant eller bro.
Note: Lad G være en graf med n hjørner:
- En sammenhængende graf G kan højst have (n-1) afskårne kanter.
- Fjernelse af en afskåret kant kan efterlade en graf usammenhængende.
- Fjernelse af en kant kan øge antallet af komponenter i en graf med højst én.
- En afskåret kant “e” må ikke være en del af nogen cyklus i G.
- Hvis der findes en afskåret kant, må der også findes et afskåret toppunkt, fordi mindst ét toppunkt i en afskåret kant er et afskåret toppunkt.
- Hvis der findes et afskåret toppunkt, er det ikke nødvendigt, at der findes en afskåret kant.
Eksempel 1
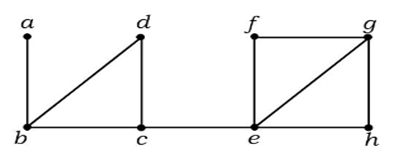
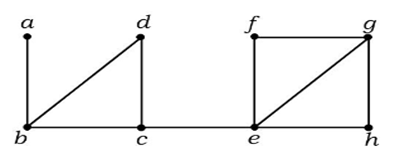
I ovenstående graf er kanten (c, e) en afskåret kant. Når denne kant er fjernet fra ovenstående graf, vil grafen blive en usammenhængende graf.
Eksempel 2
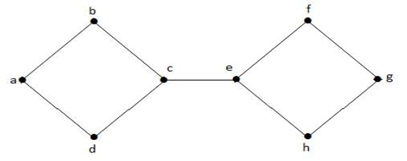
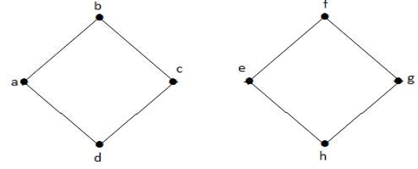
I ovenstående graf er kant (c, e) en afskåret kant. Når denne kant er fjernet fra ovenstående graf, bliver grafen en usammenhængende graf.
Cut Set
I en sammenhængende graf G er et cut set et sæt S af kanter med følgende egenskaber:
- Fjernelse af alle kanter i S afbryder forbindelsen til G.
- Fjernelse af nogle af kanterne (men ikke alle) i S afbryder ikke G.
Eksempel 1
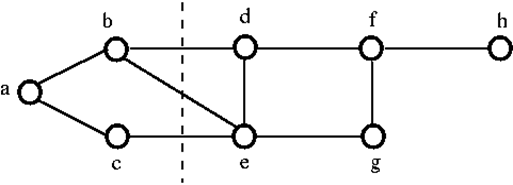
For at afbryde forbindelsen i ovenstående graf G skal vi fjerne de tre kanter, dvs. bd, be og ce. Vi kan ikke afbryde den ved kun at fjerne to af de tre kanter. Derfor er {bd, be, ce} et snittet sæt.
Når vi fjerner det snittede sæt fra ovenstående graf, vil den se ud som følger:
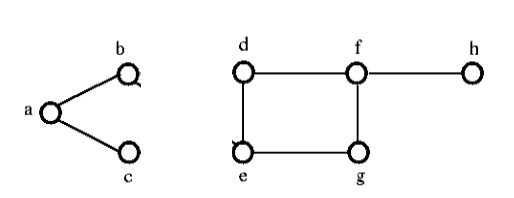
Edge Connectivity
Kantkonnektiviteten af en sammenhængende graf G er det mindste antal kanter, hvis fjernelse gør G usammenhængende. Det betegnes med λ(G).
Når λ(G) ≥ k, siges grafen G at være k-kantforbundet.
Eksempel
Lad os se et eksempel,
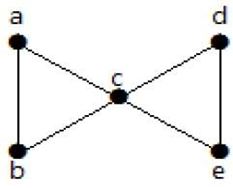
Fra ovenstående graf, ved at fjerne to minimumskanter, bliver den forbundne graf til en frakoblet graf. Derfor er dens kantkonnektivitet 2. Derfor er ovenstående graf en 2-kantforbundet graf.
Her er følgende fire måder at afbryde grafen på ved at fjerne to kanter:
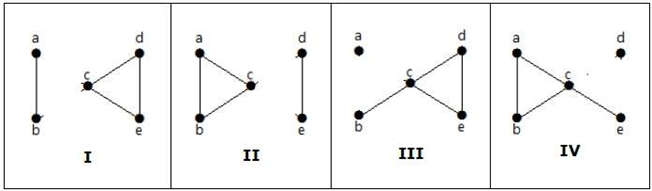
Vertex Connectivity
Konnektiviteten (eller vertex connectivity) af en forbundet graf G er det mindste antal hjørner, hvis fjernelse gør, at G afbrydes eller reduceres til en trivial graf. Det betegnes med K(G).
Grafen siges at være k-tilsluttet eller k-vertex-tilsluttet, når K(G) ≥ k. For at fjerne et toppunkt skal vi også fjerne de kanter, der er tilknyttet det.
Eksempel
Lad os se et eksempel:
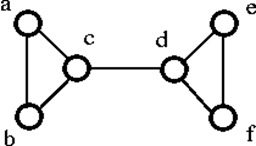
Overstående graf G kan frakobles ved at fjerne det enkelte toppunkt enten “c” eller “d”. Derfor er dens toppunktsforbindelse 1. Derfor er det en 1-forbundet graf.