Kemisk kinetik
Kemisk kinetik
Du er måske bekendt med syre-base-titreringer, hvor der anvendes phenolphthalein som endepunktsindikator. Men du har måske ikke bemærket, hvad der sker, når en opløsning, der indeholder phenolphthalein i tilstedeværelse af et overskud af base, får lov til at stå i et par minutter. Selv om opløsningen i begyndelsen har en lyserød farve, bliver den gradvist farveløs, når phenolphthalein reagerer med OH-ionen i en stærkt basisk opløsning.
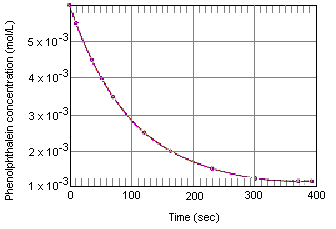
Tabellen nedenfor viser, hvad der sker med koncentrationen af phenolphthalein i en opløsning, der oprindeligt var 0,005 M i phenolphthalein og 0,61 M i OH-ion. Som du kan se, når disse data er plottet ind i nedenstående graf, falder phenolphthaleinkoncentrationen med en faktor 10 over en periode på ca. fire minutter.
Eksperimentelle data for reaktionen mellem phenolphthalein og overskudsbase
Eksperimenter som det, der gav os dataene i ovenstående tabel, klassificeres som målinger af kemisk kinetik (fra en græsk stamme, der betyder “tomove”). Et af målene med disse eksperimenter er at beskrive reaktionshastigheden den hastighed, hvormed reaktanterne omdannes til reaktionens produkter.
Begrebet hastighed bruges ofte til at beskrive den ændring i en mængde, der sker pr. tidsenhed. Inflationsraten er f.eks. ændringen i gennemsnitsomkostningerne for en samling af standardartikler pr. år. Den hastighed, hvormed et objektbevæger sig gennem rummet, er den tilbagelagte afstand pr. tidsenhed, f.eks. miles pr. time eller kilometer pr. sekund. I kemisk kinetik er den tilbagelagte afstand ændringen i koncentrationen af en af reaktionens komponenter. En reaktionshastighed er derfor den ændring i koncentrationen af en af reaktanterne![]() (X)
(X)![]() , der sker i løbet af et givet tidsrum
, der sker i løbet af et givet tidsrum![]() t.
t.
![]()
Praksisopgave 1:
Brug dataene i ovenstående tabel til at beregne den hastighed, hvormed phenolphthalein reagerer med OH-ionen i hvert af følgende tidsintervaller:
(a) I det første tidsinterval, hvor phenolphthaleinkoncentrationen falder fra 0,0050 M til 0,0045 M.
(b) I det andet tidsinterval, når koncentrationen falder fra 0,0045 M til 0,0040 M.
(c) I det tredje tidsinterval, når koncentrationen falder fra 0,0040 M til 0,0035 M.
Klik her for at kontrollere dit svar til øvelsesopgave 1.
Klik her for at se en løsning til øvelsesopgave 1.
![]()
Instant reaktionshastighed og hastighedsloven for en reaktion
Reaktionshastigheden for reaktionen mellem phenolphthalein og OH-ionen er ikke konstant; den ændrer sig med tiden. Som de fleste reaktioner falder hastigheden af denne reaktion gradvist, efterhånden som reaktanterne forbruges. Det betyder, at reaktionshastigheden ændrer sig, mens den måles.
For at minimere den fejl, som dette medfører i vores målinger, synes det tilrådeligt at måle reaktionshastigheden over tidsperioder, der er korte i forhold til den tid, det tager for reaktionen at finde sted. Vi kan f.eks. forsøge at måle den uendeligt lille ændring i koncentrationen![]() d(X)
d(X)![]() , der sker i løbet af en uendeligt kort tidsperiode. Forholdet mellem disse mængder er kendt som den øjeblikkelige reaktionshastighed.
, der sker i løbet af en uendeligt kort tidsperiode. Forholdet mellem disse mængder er kendt som den øjeblikkelige reaktionshastighed.
![]()
Den øjeblikkelige reaktionshastighed på et hvilket som helst tidspunkt kan beregnes ud fra en graf over koncentrationen af reaktanten (eller produktet) i forhold til tiden. Nedenstående graf viser, hvordan reaktionshastigheden for nedbrydning af phenolphthalein kan beregnes ud fra en graf over koncentrationen i forhold til tiden. Reaktionshastigheden på et hvilket som helst tidspunkt i tiden er lig med hældningen af en tangent til denne kurve på det pågældende tidspunkt.
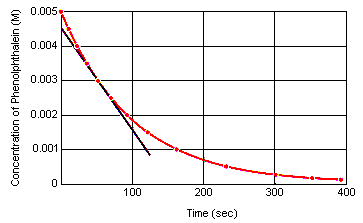
Den øjeblikkelige reaktionshastighed kan måles på et hvilket som helst tidspunkt mellem det tidspunkt, hvor reaktanterne blandes, og det tidspunkt, hvor reaktionen når ligevægt.Ved at ekstrapolere disse data tilbage til det tidspunkt, hvor reagenserne blandes, fås den oprindelige øjeblikkelige reaktionshastighed.
![]()
Rate Laws and Rate Constants
Et interessant resultat fås, når den øjeblikkelige reaktionshastighed beregnes på forskellige punkter langs kurven i grafen i det foregående afsnit. Reaktionshastigheden i hvert punkt på denne kurve er direkte proportional med koncentrationen af phenolphthalein på det pågældende tidspunkt.
Rate = k(phenolphthalein)
Da denne ligning er en eksperimentel lov, der beskriver reaktionshastigheden, kaldes den for reaktionshastighedsloven for reaktionen. Proportionalitetskonstanten, k, er kendt som hastighedskonstanten.
Praksisopgave 2:
Beregn hastighedskonstanten for reaktionen mellem phenolphthalein og OH-ionen, hvis den øjeblikkelige reaktionshastighed er 2,5 x 10-5 mol pr. liter pr. sekund, når koncentrationen af phenolphthalein er 0,0025 M.
Klik her for at tjekke dit svar til praksisopgave 2.
Klik her for at se en løsning til praksisopgave 2.
Praksisopgave 3:
Anvend hastighedskonstanten for reaktionen mellem phenolphthalein og OH-ionen til at beregne den indledende øjeblikkelige reaktionshastighed for de eksperimentelle data, der er anført i den foregående tabel.
Klik her for at kontrollere dit svar på øvelsesopgave 3.
Klik her for at se en løsning på øvelsesopgave 3.
![]()
Differente måder at udtrykke reaktionshastigheden på
Der er normalt mere end én måde at måle en reaktionshastighed på. Vi kan f.eks. undersøge nedbrydningen af hydrogeniodid ved at måle den hastighed, hvormed enten H2 eller I2 dannes i den følgende reaktion, eller den hastighed, hvormed HI forbruges.
2 HI(g) H2(g) + I2(g)
Eksperimentelt finder vi, at den hastighed, hvormed I2 dannes, er proportionel med kvadratet på HI-koncentrationen på et hvilket som helst tidspunkt.
![]()
Hvad ville der ske, hvis vi undersøgte den hastighed, hvormed H2 dannes?Den balancerede ligning antyder, at H2 og I2 må dannes med nøjagtig samme hastighed.
![]()
Hvad ville der imidlertid ske, hvis vi undersøgte den hastighed, hvormed HI forbruges i denne reaktion? Fordi HI forbruges, må ændringen i dens koncentration være et negativt tal. Konventionelt angives hastigheden af en reaktion altid som et positivt tal. Vi er derfor nødt til at ændre fortegnet, før vi rapporterer reaktionshastigheden for et stof, der forbruges i reaktionen.
![]()
Det negative fortegn gør to ting. Matematisk set omdanner det en negativændring i koncentrationen af HI til en positiv hastighed. Fysisk minder det os om, at koncentrationen af reaktanten falder med tiden.
Hvad er forholdet mellem den reaktionshastighed, der fremkommer ved at overvåge dannelsen af H2 eller I2, og den hastighed, der fremkommer ved at overvåge HI forsvinde? Støkiometrien for reaktionen siger, at der forbruges to HI-molekyler for hvert molekyle H2 eller I2, der dannes. Det betyder, at hastigheden for nedbrydning af HI er dobbelt så hurtig som den hastighed, hvormed H2 og I2 dannes. Vi kan omsætte dette forhold til en matematisk ligning på følgende måde.
![]()
Som følge heraf er den hastighedskonstant, der fås ved at studere den hastighed, hvormed H2og I2 dannes i denne reaktion (k), ikke den samme som den hastighedskonstant, der fås ved at overvåge den hastighed, hvormed HI forbruges (k’)
Praksisopgave 4:
Beregn den hastighed, hvormed HI forsvinder i den følgende reaktion på det tidspunkt, hvor I2 dannes med en hastighed på 1.8 x 10-6 mol pr. liter pr. sekund:
2 HI(g) ![]() H2(g) + I2(g)
H2(g) + I2(g)
Klik her for at kontrollere dit svar til øvelsesopgave 4.
Klik her for at se en løsning til øvelsesopgave 4.
![]()
Rate Law Versus the Stoichiometry of aReaction
I 1930’erne undersøgte Sir Christopher Ingold og medarbejdere på University ofLondon kinetikken af substitutionsreaktioner som f.eks.
CH3Br(aq) + OH-(aq)
CH3OH(aq) + Br-(aq)
De fandt, at hastigheden af denne reaktion er proportional medkoncentrationerne af begge reaktanter.
Sats = k(CH3Br)(OH-)
Da de kørte en lignende reaktion på et lidt anderledes udgangsmateriale, fik de lignende produkter.
(CH3)3CBr(aq) + OH-(aq)![]() (CH3)3COH(aq) + Br-(aq)
(CH3)3COH(aq) + Br-(aq)
Men nu var reaktionshastigheden proportional med koncentrationen af kun én af reaktanterne.
Rate = k((CH3)3CBr)
Disse resultater illustrerer et vigtigt punkt: Hastighedsloven for en reaktion kan ikke forudsiges ud fra reaktionens støkiometri; den skal bestemmes eksperimentelt. Nogle gange er hastighedsloven i overensstemmelse med det, vi forventer ud fra reaktionens stoiometri.
2 HI(g) H2(g) + I2(g)
Sats = k(HI)2
Ofte, er det imidlertid ikke.
| 2 N2O5(g) |
Rate = k(N2O5) |
![]()
Molekylærhedsorden
Nogle reaktioner foregår i et enkelt trin. Reaktionen, hvor et kloratatom overføres fra ClNO2 til NO for at danne NO2 og ClNO, er et godt eksempel på en reaktion i ét trin.
ClNO2(g) + NO(g)
NO2(g) + ClNO(g)
Andre reaktioner sker ved en række individuelle trin. N2O5 nedbrydes f.eks. til NO2 og O2 ved en tretrinsmekanisme.
| Strin 1: | N2O5 |
||
| Strin 2: | NO2 + NO3 |
||
| Stræk 3: | NO + NO3 |
Trinene i en reaktion klassificeres efter molekularitet, som beskriver antallet af molekyler, der forbruges. Når der kun forbruges et enkeltmolekyle, kaldes trinnet for unimolekylært. Når der forbruges to molekyler, er det bimolekylært.
Praksisopgave 5:
Bestem molekulariteten af hvert trin i den reaktion, hvorved N2O5 nedbrydes til NO2 og O2.
Klik her for at kontrollere dit svar på praksisopgave 5.
Klik her for at se en løsning på praksisopgave 5.
Reaktioner kan også klassificeres efter deres rækkefølge. Nedbrydningen af N2O5 er en reaktion af første orden, fordi reaktionshastigheden afhænger af koncentrationen af N2O5 i første potens.
Rate = k(N2O5)
Den nedbrydning af HI er en reaktion af anden orden, fordi reaktionshastigheden afhænger af koncentrationen af HI i anden potens.
Rate = k(HI)2
Når hastigheden af en reaktion afhænger af mere end enreagens, klassificerer vi reaktionen i forhold til rækkefølgen af hver enkeltreagens.
Praksisopgave 6:
Klassificer rækkefølgen af reaktionen mellem NO og O2 til dannelse af NO2:
2 NO(g) + O2(g) ![]() 2 NO2(g)
2 NO2(g)
Antag følgende hastighedslov for denne reaktion:
Rate = k(NO)2(O2)
Klik her for at tjekke dit svar til praksisopgave 6.
Forskellen mellem en reaktions molekylaritet og reaktionsorden er vigtig. Molekulariteten af en reaktion, eller et trin i en reaktion, beskriver, hvad der sker på molekylært niveau. Rækkefølgen af en reaktion beskriver, hvad der sker på makroskopisk niveau. Vi bestemmer rækkefølgen af en reaktion ved at se, hvordan reaktionens produkter opstår, eller hvordan reaktanterne forsvinder. Reaktionens molekylære karakter er noget, vi udleder for at forklare disse eksperimentelle resultater.
![]()
Kollisionsteorimodel for kemiske reaktioner
Kollisionsteorimodellen for kemiske reaktioner kan bruges til at forklare de observerede hastighedslove for både et-trins- og flertrinsreaktioner. Denne model forudsætter, at hastigheden for ethvert trin i en reaktion afhænger af hyppigheden af kollisioner mellem de partikler, der er involveret i det pågældende trin.
Figuren nedenfor giver et grundlag for at forstå konsekvenserne af den kollisionsteoretiske model for simple, et-trinsreaktioner som f.eks. den følgende.
ClNO2(g) + NO(g) ![]() NO2(g) + ClNO(g)
NO2(g) + ClNO(g)
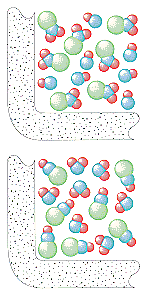
Den kinetiske molekyleteori forudsætter, at antallet af kollisioner pr. sekund i en gas afhænger af antallet af partikler pr. liter. Den hastighed, hvormed NO2og ClNO dannes i denne reaktion, bør derfor være direkte proportional med koncentrationerne af både ClNO2 og NO.
Rate = k(ClNO2)(NO)
Den kollisionsteoretiske model antyder, at hastigheden af ethvert trin i en reaktion er proportional med koncentrationerne af de reagenser, der forbruges i det pågældende trin. Hastighedsloven for en reaktion i et enkelt trin bør derfor stemme overens med reaktionens støkiometri.
Følgende reaktion foregår f.eks. i et enkelt trin.
CH3Br(aq) + OH-(aq) ![]() CH3OH(aq) + Br-(aq)
CH3OH(aq) + Br-(aq)
Når disse molekyler støder sammen i den rette retning, kan et par ikke-bundende elektroner på OH-ionen doneres til kulstofatomet i midten af CH3Br-molekylet, som vist i figuren nedenfor.
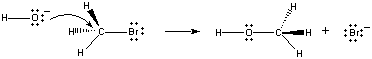
Når dette sker, dannes der en kulstof-oxygenbinding samtidig med, at kulstof-brom-bindingen brydes. Nettoresultatet af denne reaktion er udskiftning af enOH- ion med en Br – ion. Fordi reaktionen sker i et enkelt trin, hvilket indebærer kollisioner mellem de to reaktanter, er hastigheden af denne reaktion proportionel med koncentrationen af begge reaktanter.
Rate = k(CH3Br)(OH-)
Det er ikke alle reaktioner, der sker i et enkelt trin. Følgende reaktion foregår i tre trin, som vist i figuren nedenfor.
(CH3)3CBr(aq) + OH-(aq)![]() (CH3)3COH(aq) + Br-(aq)
(CH3)3COH(aq) + Br-(aq)
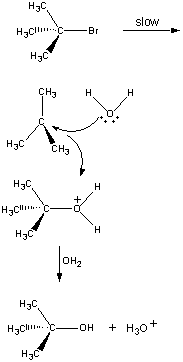
I det første trin dissocieres (CH3)3CBr-molekylet til et par ioner.
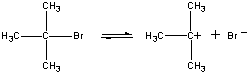 |
Den positivt ladede (CH3)3C+-ion reagerer derefter med vand i et andet trin.
| Second step | 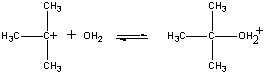 |
Produktet af denne reaktion taber derefter en proton til enten OH-ionen eller vand i det sidste trin.
| Tredje trin | 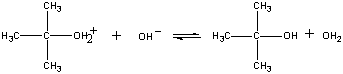 |
Det andet og tredje trin i denne reaktion er meget meget hurtigere endførste.
| (CH3)3CBr |
Slow step | ||
| (CH3)3C+ + H2O |
Fast step | ||
| (CH3)3COH2+ + OH- |
Hurtigt trin |
Den samlede reaktionshastighed er derfor mere eller mindre lig med hastigheden af det første trin. Det første trin kaldes derfor det hastighedsbegrænsende trin i denne reaktion, fordi det bogstaveligt talt begrænser den hastighed, hvormed reaktionens produkter kan dannes. Da kun én reagens er involveret i det hastighedsbegrænsende trin, er den samlede reaktionshastighed proportional med koncentrationen af kun denne reagens.
Rate = k((CH3)3CBr)
Hastighedsloven for denne reaktion adskiller sig derfor fra det, som vi ville forudsige ud fra reaktionens stoikiometri. Selv om reaktionen forbruger både (CH3)3CBrand OH-, er reaktionshastigheden kun proportional med koncentrationen af(CH3)3CBr.
Hastighedslovene for kemiske reaktioner kan forklares ved følgende generelle regler.
Hastigheden af et hvilket som helst trin i en reaktion er direkte proportional med koncentrationerne af de reagenser, der forbruges i dette trin.
Den samlede hastighedslov for en reaktion bestemmes af den rækkefølge af trin, eller mekanisme, hvormed reaktanterne omdannes til reaktionens produkter.
Den samlede hastighedslov for en reaktion domineres af hastighedsloven for det langsomste trin i reaktionen.