Hvor mange sider har en cirkel?

Det er et lektiehjemmespørgsmål fra folkeskolen, som giver anledning til uenighed blandt erfarne matematikere. For at finde det korrekte svar har jeg benyttet mig af det mest stringente videnskabelige instrument, Twitter-afstemningen:

I retrospekt fortryder jeg, at jeg ikke inkluderede en “ingen af de ovennævnte” mulighed, men mere om det senere. I dette indlæg vil jeg gennemgå disse tre svar (og “Ingen af de ovennævnte”) og diskutere deres fordele og ulemper, som jeg ser dem, inden jeg dramatisk afslører det korrekte svar.

Men først: Hvorfor kan vi ikke direkte give det rigtige svar? Ordene i spørgsmålet er næppe mystiske. Vi ved alle sammen, hvad en “cirkel” er, hvad det vil sige at tælle “hvor mange” af noget, og hvad en “side” er … eller gør vi ikke? Her er de (grove) definitioner, som jeg har fået ud af diskussioner med to elever i folkeskolen, der har fået dette spørgsmål:

1. En linje, der udgør en del af en forms afgrænsning af en plan figur.

Sigtet med at sige plan figur i stedet for “form” her er, at vi ønsker former, der lever i 2-dimensioner (f.eks. firkanter eller cirkler, men ikke kugler eller terninger). Det næste spørgsmål er, hvad en “linje” er i definition 1. Her er en variant, der fastlægger det:

2. En lige linje, der udgør en del af grænsen for en plan figur.

Hvis du skriver “define: side” i Google, er den mest relevante definition:

En retlinet figur er en figur, der er opbygget af lige linjer. Denne definition er altså en yderligere forfinelse af definition 2 og giver os mulighed for at bekræfte, at et kvadrat har fire sider, men har umiddelbart intet at sige om ikke-rekttilineære plane figurer som f.eks. cirkler.

Uendeligt mange sider?

Jeg tror, at det er et sikkert bud, at de, der har svaret på min Twitter-afstemning, har et højere matematisk uddannelsesniveau end landsgennemsnittet. Det faktum, at de overhovedet var splittede på dette spørgsmål, og at et lille flertal valgte et svar, som er temmelig utilgængeligt for dette spørgsmåls sædvanlige målgruppe (grundskoleelever), tyder helt sikkert på, at der er noget, der går galt et eller andet sted.

Så, har en cirkel uendeligt mange sider? Det er bestemt nyttigt at betragte en cirkel som grænsen for n-sidede polygoner, efterhånden som n bliver større og større. Det er præcis den tilgang, som Archimedes, Liu Hui og utallige andre har brugt gennem århundrederne til at studere cirkelgeometri, herunder til at finde frem til tilnærmelser for π.

En udgave fra det 16. århundrede fra Ming-dynastiet af Jiuzhang suanshu (Ni kapitler om den matematiske kunst), tredje århundrede e.Kr.

Sommetider er det absolut fornuftigt, som en bekvem forkortelse, at tænke på en cirkel som værende som en polygon med uendeligt mange sider.

Men som en ulidelig pedant en matematiker, vil jeg gerne skelne mellem bekvem forkortelse og bogstavelig sandhed. Hvis vi holder fast i, at en cirkel virkelig er en polygon med uendeligt mange sider, så melder spørgsmålet sig: Hvilke sider er det? Og det eneste plausible svar er vel, at det er de enkelte punkter i cirklen. Hvor lange er disse såkaldte sider? Nul centimeter. Og er disse sider adskilt af hjørner? Tilsyneladende ikke, enten er der slet ingen hjørner, eller også er hvert punkt både en side og et hjørne.

Jeg vil sige, at sider af længde nul er … et problematisk begreb. Hvordan kan man se, om man har fået nogen? Lad os for eksempel antage, at jeg studerer et system, hvor et kvadrat opstår som en grænse af ottekanter på denne måde:

I denne situation kunne det godt give mening for mig at tænke på mit kvadrat som havende otte sider, hvoraf fire har længde nul. Men hvis jeg insisterede på, at mit (helt almindelige) kvadrat virkelig har otte sider, ville du måske løfte et øjenbryn.

Så dette – det vindende svar i min afstemning – er det eneste svar, som jeg vil erklære for definitivt forkert, samtidig med at det også er det eneste, som giver nogen geometrisk indsigt overhovedet. Et paradoks? Egentlig ikke. At ræsonnere ved hjælp af analogier er en værdifuld færdighed i matematikken og i livet; samtidig er det vigtigt at holde fast i erkendelsen af, at det er det, vi gør.

For uendeligt mange sider: geometrisk oplysende.
Med uendeligt mange sider: ottesidede firkanter.

Op en tangent 1: apeirogoner

Selv om en cirkel ikke er en cirkel, findes der så polygoner med uendeligt mange sider? Tja, der findes et ord til at beskrive sådan en ting en apeirogon. En regulær apeirogon ville så have sider af samme (ikke-nul) længde med lige store vinkler mellem dem. Den eneste mulighed her er dette utroligt uinteressante objekt:

Hvis du har indvendinger mod, at dette er en “polygon” (enten på grund af vinklerne på 180° eller fordi kæden af kanter ikke slutter i en løkke), hvad så med noget i stil med dette: start i bunden af en cirkel, og bevæg dig ved hvert trin rundt om halvdelen af det, der er tilbage af cirklen, og erstat den bue, du lige har tilbagelagt, med en lige kant:

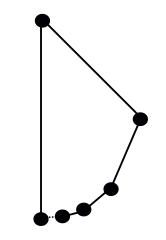
Er dette en ægte polygon? Endnu en gang afhænger det af dine begreber. Ifølge en almindelig definition, nemlig definitionen af en “lukket polygonal kæde”, opfylder dette ikke betingelserne, da starthjørnet (nederst til venstre) kun har forbindelse til én kant. Men det er meget tæt på: dette punkt er grænsen for en sekvens af kanter fra højre, hvilket gør denne form til en “ikke-selvskærende stykkevis lineær lukket kurve”, en anden definition af polygon, som folk bruger.

Hvis vi forlader vores sædvanlige euklidiske verden og træder ind i det hyperbolske rum, er der ingen tvetydighed. Apeirogoner (selv regelmæssige apeirogoner) eksisterer simpelthen:

En flisebelægning af det hyperbolske plan af regelmæssige apeirogoner. (Af Anton Sherwood – Eget arbejde, Public Domain, https://commons.wikimedia.org/w/index.php?curid=13260274 )

Off on a tangent 2: extreme points

Det er måske mere forsvarligt at sige, at en cirkel har uendeligt mange hjørner end uendeligt mange sider (selv om det ikke er et spørgsmål, der synes at blive stillet særlig ofte). Til at begynde med, hvis et hjørne af et kvadrat er et punkt, hvor dets grænselinje ikke er lige, så opfylder ethvert punkt på cirklen dette. Mere sofistikeret er der et begreb om et ekstremt punkt på en form: det er ethvert punkt, hvorigennem man kan tegne et retlinjesegment, som kun berører formen i netop dette punkt. For et kvadrat og mange kendte figurer falder yderpunkterne nøjagtigt sammen med hjørnerne. Ethvert punkt på cirklens grænse er et yderpunkt, så det er helt sikkert sandt, at en cirkel har uendeligt mange.

Vi kan bekymre os om, at nogle former som denne chevron har hjørner, der ikke er yderpunkter:

Her er det nederste centrale hjørne ikke et yderpunkt (de tre andre hjørner er det). Det, der går galt, er, at denne form ikke er konveks (groft sagt, den har nogle stykker, der stikker for langt ud). En cirkel er konveks, så måske behøver vi ikke at bekymre os. Alternativt kan vi afhjælpe situationen ved at definere et “hjørne” som et punkt, der er et yderpunkt enten af den pågældende form eller af dens komplement, dvs. hele planen med formen skåret ud af den. På den måde ville man opdage hjørner af alle polygoner, også chevronerne. For glatte kurver ville den identificere alle grænsepunkter som “hjørner” med undtagelse af bøjningspunkter (hvilket ikke er urimeligt, da vi kan argumentere for, at grænsen er lige der).

En side?

I folkeskolen er det tilsyneladende sådan, at “en” er det svar, der får krydset. Og der er en nogenlunde anstændig begrundelse. Husk definition 1 ovenfor:

1. En linje, der udgør en del af afgrænsningen af en plan figur.

Det umiddelbare spørgsmål er, hvad der tæller som en “linje”, især hvis vi ikke insisterer på rethed. Hvis vi er for afslappede med hensyn til dette, kan enhver plan figur siges at have “én side”, i samme forstand som den har én afgrænsning, omkreds eller omkreds. Men det må være forkert, da vi helt sikkert ønsker, at et kvadrat skal have fire sider. Nå, men et kvadrat har fire punkter, hvor det ikke er glat, med fire glatte dele i mellem. Måske var det i virkeligheden de glatte dele, som vi hele tiden har talt med. Så implicit har vi en ny forfinelse af definition 1 (og benytter også lejligheden til at droppe det vage begreb “figur”):

4. Hvert glat afsnit af en stykkevis glat lukket kurve.

En “lukket kurve” er en kurve, der løber rundt for at mødes med sig selv, så den ikke har nogen frie ender. “Stykkevis glat” betyder, at den er opbygget af glatte afsnit, som mødes i isolerede uglatte punkter. Det er helt legitimt at ville tælle de glatte dele af en sådan forms grænse, og det er på ingen måde skandaløst at bruge ordet “side”, når man gør det. Så jeg siger bestemt ikke, at dette er et definitivt forkert svar.

Spørgsmålet er, om denne fortolkning af “side” ikke blot er kohærent, men naturlig nok til, at den blot kan formodes uden at blive angivet eksplicit (hvilket den sjældent eller aldrig er). Hvad sker der, når glathed og rethed tæller forskelligt op? Tag denne gravstensform, der er skabt ved at erstatte toppen af et kvadrat med en halvcirkel af samme diameter.

Dette har to glatte sektioner (den nederste linje og resten), men tre lige kanter (plus et buet stykke, der glat forbinder to af dem). Hvor mange sider har den så? Jeg konsulterede mine Twitter-venner igen:

Denne gang burde jeg have medtaget “uendeligt mange” som en mulighed, selv om det kan absorberes i “Ingen af ovenstående”. Enhver, der stemmer på, at cirklen har uendeligt mange sider, bør automatisk stemme “Ingen af ovenstående” her, medmindre – et vigtigt forbehold – denne forms karakter indikerer, at læseren har et andet begreb om “side”. Det faktum, at de mest populære valg i disse to afstemninger er uforenelige, tyder på, at dette kan være tilfældet (eller i det mindste forstærker det, at vandene er mudrede).

Men selv om to er et helt respektabelt svar, der er foreneligt med definition 4 ovenfor og med en cirkels ensidighed, er jeg ikke overbevist om, at det er det endegyldigt rigtige, eller at tre eller fire er kategorisk forkerte. Det afhænger af, hvad man vil tælle: glatte sektioner, lige kanter eller lige kanter plus det, der så er tilbage, hvilket alt efter kontekst kan være det svar, man ønsker (mere herom nedenfor). I forbindelse hermed er jeg ikke sikker på, at det at tælle antallet af glatte sektioner fuldt ud stemmer overens med min intuition af ordet “side”. Gravstenens to opretstående sektioner er trods alt – jeg synes, det er rimeligt at sige – “på modsatte sider”. Er vi virkelig tilfredse med, at de samtidig er en del af “samme side”?

Du vil måske protestere mod, at jeg blander to forskellige betydninger af “side” sammen, at terminologien nogle gange støder sammen, og at vi bare må leve med det. Jeg er dog ikke så sikker. Pointen med denne øvelse er at ekstrapolere fra en situation (retlinede figurer), hvor de to begreber passer ret godt sammen. Hvis der var en ny idé, som indeholdt alt det, vi kunne lide ved den oprindelige idé, men som også gjaldt for en bredere kategori af figurer, ville den have et overvældende krav på at være det eneste rigtige svar. Men hvis alle vores forsøg på at generalisere indebærer, at vi må ofre ønskværdige aspekter af den oprindelige form, så findes der måske ikke en enkelt korrekt generalisering. Der er forskellige valgmuligheder, med forskellige kompromiser, som kan være velegnede i forskellige sammenhænge (og hvis vi er i en situation, hvor mere end én er i spil, så kunne de med fordel gives forskellige navne).

Her er en anden variation: en Weierstrass-gravsten skabt ved at erstatte den øverste kant af et kvadrat med et udsnit af Weiestress-funktionen, en uendeligt slingrende linje, som ikke er glat nogen steder.

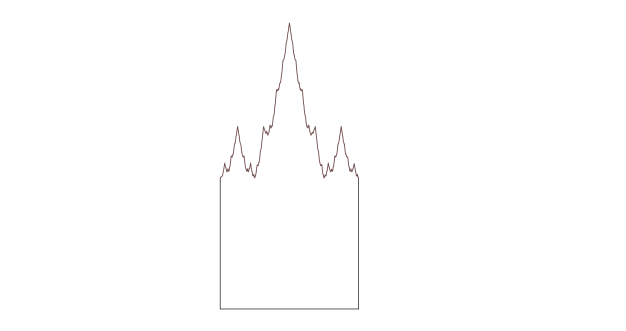
Her (og spot the typo) er, hvad mine Twitter-venner gjorde ud af dette – selv om færre vovede en mening:

Trods mine Twitter-følgeres skepsis vil jeg om et øjeblik forklare, hvorfor jeg ikke synes, det er dumt at se dette som havende fire sider (hvoraf den ene er ikke glat). På den anden side, hvis du foretrækker dine sider glatte, så har du igen et valg mellem at se den som havende uendeligt mange sider (hvoraf tre har længde 1, og resten har længde 0), eller som havende 3 sider plus en strækning af helt sikkert-ikke-en-side grænsen.

Til en side: en enkelt glat kurve.
Med en side: den samme side på modsatte sider.

Op en tangent 3: sider versus kanter

Hvor mange sider har et kvadrat? 4. Hvor mange kanter har det? Fire. Er kanter og sider så det samme? Ikke nødvendigvis. Her er to konfigurationer, som – i det mindste kan man argumentere for – hver især har fire sider, men som har henholdsvis 5 og 3 kanter:

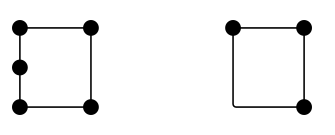
Sædvanligvis vil jeg sige, at en “kant” er et topologisk objekt, idet det er dens funktion og ikke dens form, der er afgørende. Tænk på Londons metrokort. Hvis du spurgte, hvor mange kanter der er i det netværk, er der ingen fortjeneste i at tælle lige eller glatte strækninger op. Det er forbindelserne mellem stationerne (eller hjørnerne), der tæller.

Som allerede nævnt er det almindeligt at betragte en polygon som en meget simpel form for netværk, der kaldes en lukket polygonal kæde: en række hjørner (i dette tilfælde polygonens hjørner), der er forbundet med kanter på en sådan måde, at hvert hjørne ligger på præcis to kanter, og det hele danner en enkelt løkke. I denne situation falder kanter og sider sammen, og det samme gør hjørner og hjørner. Men generelt kan man bryde dette sammenfald, som i de to små netværk ovenfor.

Hvis man ønsker at tænke netværksteoretisk, men hjørnerne ikke er tydeligt markeret, må man gætte sig frem til, hvor de er. Med en polygon er dette let – toppene er i hjørnerne – og det er derfor, at det er så naturligt at skifte mellem geometriske og topologiske tilgange. Men med andre figurer, som f.eks. en af de to gravsten ovenfor, er det måske ikke så indlysende. Ikke desto mindre tror jeg, at hvis man i hvert af tilfældene fik at vide, at der var toppunkter et sted derinde og blev bedt om at lokalisere dem, ville det være fornuftigt at gætte på, at der er fire, nemlig hjørnerne af det oprindelige kvadrat, og at den øverste kant af en eller anden grund er blevet repræsenteret som en ikke lige linje. Og hvis vi ønsker at tænke på tingene på den måde, at hver af gravstenene har fire kanter, så kan det virke perverst (om end logisk sammenhængende!) for at insistere på, at de har et andet antal sider (især fordi den øverste side – på trods af sin egen geometri – klart er “på den ene side” af figuren). I stedet for at gætte spurgte en af mine Twitter-korrespondenter mig faktisk: “Er begge øverste hjørner blevet fjernet?”, et spørgsmål, som kun giver mening ud fra et netværksteoretisk perspektiv.

Hvor efterlader dette cirklen? Problemet er, at intet punkt på cirklen har et bedre krav på at være toppunkt end noget andet. Så selv om det er fristende (og igen sammenhængende) at betragte en cirkel som et netværk med én kant, er der, hvis vi skal indsætte toppunkter, ingen indlysende grund til at foretrække ét frem for et andet tal.

Kunne vi betragte den som et netværk uden toppunkter overhovedet, en slags metrolinje uden stationer? Den sædvanlige matematiske opfattelse af et netværk ville ikke tillade det, men det bør ikke afskrække os for meget. Det tyder på en rent topologisk tilgang. Problemet er, at ud fra dette synspunkt kan en cirkel være en slags netværk uden toppunkter og med én kant, men det er et kvadrat også (hvis det er sådan, at metrolinjen tilfældigvis er udformet). I topologi er et kvadrat en cirkel. (Dette er ikke et paradoks, det er blot at sige, at grænsen er en enkelt løkke, hvis form er ligegyldig). Så selv om denne form for netværk har “én kant”, har et kvadrat naturligvis ikke “én side”, så forholdet mellem sider (geometrisk) og kanter (topologisk) er igen brudt sammen, ligesom det er tilfældet i de to små netværk, der er afbilledet ovenfor. Så denne tilgang bringer os ikke særlig langt.

Ingen sider?

Det kan virke paradoksalt at hævde, at en cirkel (eller en hvilken som helst form) ikke har “nogen sider”. Men argumentet for forsvaret er ligetil. Vi vender tilbage til definition 2:

2. En lige linje, der udgør en del af afgrænsningen af en plan figur.

Det er en enkel og let forståelig sætning, der perfekt indfanger siderne af et kvadrat. Det er ikke lykkedes os at finde en tilfredsstillende generalisering af dette til krumme figurer, så det bedste er at holde sig til det oprindelige. Og en cirkel har ingen.

For ingen sider: sandt, i henhold til et fornuftigt begreb om “side”.
Med hensyn til ingen sider: lyder som en Zen-koan.

Ingen af de ovennævnte?

Husk den definition, som Google har leveret:

3. Hver af de linjer, der danner grænsen for en plan retlinet figur.

Ved forsøg på at anvende dette på en cirkel – en ikke-rectilineær figur – kommer man ikke frem til noget. Spørgsmålet er lige så meningsløst som “Hvor mange sider har mandag?”

Da definition 3 er den mest officielle (den eneste i dette indlæg, som ikke er opfundet af mig eller mine børn), gør det så ikke “Ingen af ovenstående” kategorisk til det rigtige svar? Måske. På den anden side: Når nogen stiller os et spørgsmål, kræver princippet om velgørenhed måske, at vi antager, at det er meningsfuldt, medmindre vi med sikkerhed kan fastslå det modsatte, og definitionerne 1, 2, 4 og andre varianter gør det muligt. Endvidere er definition 3 sproglig snarere end formelt matematisk, og er derfor beskrivende snarere end foreskrivende, så vi bør ikke være bundet af den.

For ingen af ovenstående: semantisk fejlfunktion.
Med hensyn til ingen af ovenstående: dialogisk velgørenhed.

Det rigtige svar

Hvad fik mig til at skrive dette indlæg? Ligesom utallige grundskoleelever blev mine femårige tvillingesønner – de grundskoleelever, der blev nævnt i starten – for nylig stillet dette spørgsmål i deres lektier. Den ene valgte “1” og den anden “0”, og jeg har forsøgt at indfange og uddybe deres argumentation ovenfor. Jeg mener, at begge svar er fuldt ud forsvarlige – og ingen af dem er endegyldigt rigtige.

Så, hvad skal man gøre, hvis man bliver stillet spørgsmålet: Hvor mange sider har en cirkel? Efter min mening er det optimale svar at henvende sig til matematikeren i dit liv for at få ham til at skrive en afhandling på 3000 ord om emnet, som du så kan printe ud og triumferende aflevere til din uheldige lærer. Men hvis det ikke lykkes, er den bedste fremgangsmåde at følge Sokrates’ eksempel og svare på spørgsmålet med et modspørgsmål: Hvad mener du med “side”?

Når alt kommer til alt, fortæller det at tælle op til nul eller til et, eller at nægte at besvare spørgsmålet, os stort set intet om cirklernes geometri. Men der er meget at vinde ved at skille velkendte begreber ad, ved at droppe eller tilføje ekstra betingelser, ved at udfordre vores intuition ved at gå fra en sammenhæng til en lidt anden og ved at forsøge at skrive præcist ned, hvad vi mener med et bestemt begreb i en bestemt sammenhæng. Det er det, som rigtig matematik handler om.

Fodnoter

Man kunne gøre noget andet: f.eks. vælge et startpunkt P på cirklen, hvorfra man måler afstanden rundt om cirklen. Derefter erklærer man, at punkterne i en rationel afstand fra P er hjørner og resten er sider. Dette har den virkning, at man får et tælleligt uendeligt antal hjørner og et utælleligt uendeligt antal sider. Eller man kan også sige det modsatte. Dette kan være en bekvem tilpasning til den polygonale grænsetilgang til cirkler, men jeg vil have svært ved at være enig i, at det er nemt eller indlysende nok til at blive betragtet som “det rigtige svar”.

En af mine Twitter-korrespondenter var bekymret over, hvor glat kurven er. Denne gravsten er kontinuerligt differentiabel, men ikke dobbelt differentiabel. Det ville bestemt være interessant, hvis mange mente, at dette var et kritisk spørgsmål, og dette kunne sandsynligvis testes med en uendeligt glat gravsten bygget ud fra noget lignende, selv om jeg ikke har tænkt detaljerne igennem.

Vi kan forsøge at formalisere dette på følgende måde: I et kvadrat (eller en hvilken som helst polygon) har en side den egenskab, at man fra en hvilken som helst position i det indre kan skære formen lige igennem sit sted, således at den valgte side ligger fast på den ene side af snittet. Det virker ikke for den dobbeltsidede gravsten: ethvert snit vil altid skære den lange side over. Vi kunne svække dette ved at sige, at for at tælle som en side skal der være mindst én måde at skære gennem formen på, så siden ligger på den ene side af snittet. Det ville give os mulighed for at sige, at gravstenen har fire sider (selv om den buede del ikke er på den ene side af punkterne i den øverste region). For cirklen derimod er dens formodede ene side aldrig på den ene side (så den ville være udelukket), og kun den lige sektion af en halvcirkel ville tælle som en side.

Det er ikke let at komme med en stringent begrundelse, der virker for begge gravsten, men jeg tænker mere uformelt i form af Schelling-punkter: det vil sige steder, der skiller sig ud som værende specielle af grunde, der måske ikke er lette at forudsige på forhånd.

Akkommentarer

Tak til alle, der har deltaget i eller retweetet mine afstemninger eller diskuteret dette med mig på Twitter.