Røntgendiffraktion er en almindelig teknik til karakterisering af materialer, der gør det muligt at identificere krystalorienteringer og interatomare afstande. Røntgenstråler bruges til dette, fordi bølgelængden er på samme længdeskala som værdierne for interatomare mellemrum og gitterparametre.
Hvad sker der?
Røntgenstråler genereres i et vakuumrør ved at opvarme en wolframglødetråd over dens arbejdsfunktion for at udstøde elektroner. Vakuumforhold er nødvendige for at øge elektronernes gennemsnitlige frie vej. Elektronerne accelereres ind i en kobberkatode med en energi i størrelsesordenen 25 keV. Elektronernes kollisioner med kobberkatoden resulterer i ioniseringer i den indre skal og frembringer røntgenstråler, idet elektroner med højere energi falder ned for at fylde den lavere energimæssige tomrums plads. Elektroner fra forskellige højere energiniveauer falder ned og producerer elektromagnetiske bølger af varierende energi. Der dannes således røntgenstråler af flere bølgelængder (af typen K-beta og K-alpha). Ved røntgendiffraktion er det ideelt at have monokromatisk lys, der interagerer med prøven, så K-beta-røntgenstrålerne filtreres fra med en nikkelplade. Selv om der faktisk er to tilknyttede K-alpha-energier, er energierne så ens, at det ikke har nogen væsentlig indflydelse på den samlede topprofil. Røntgenstrålerne passerer gennem en kollimator for at justere strålebredden.
En lille baggrund med Braggs lov
Braggs lov beskriver forholdet for konstruktiv interferens, hvor røntgenstråler med bølgelængde λ, der falder ind på materialet i vinklen θ, diffrakteres af krystalplaner adskilt af afstanden d, og n repræsenterer et heltal.
Som vist se nedenfor forårsager en faseforskydning i bølgen enten konstruktiv interferens, som vist til venstre, eller destruktiv interferens, afbildet til højre, alt efter vinklen 2θ.
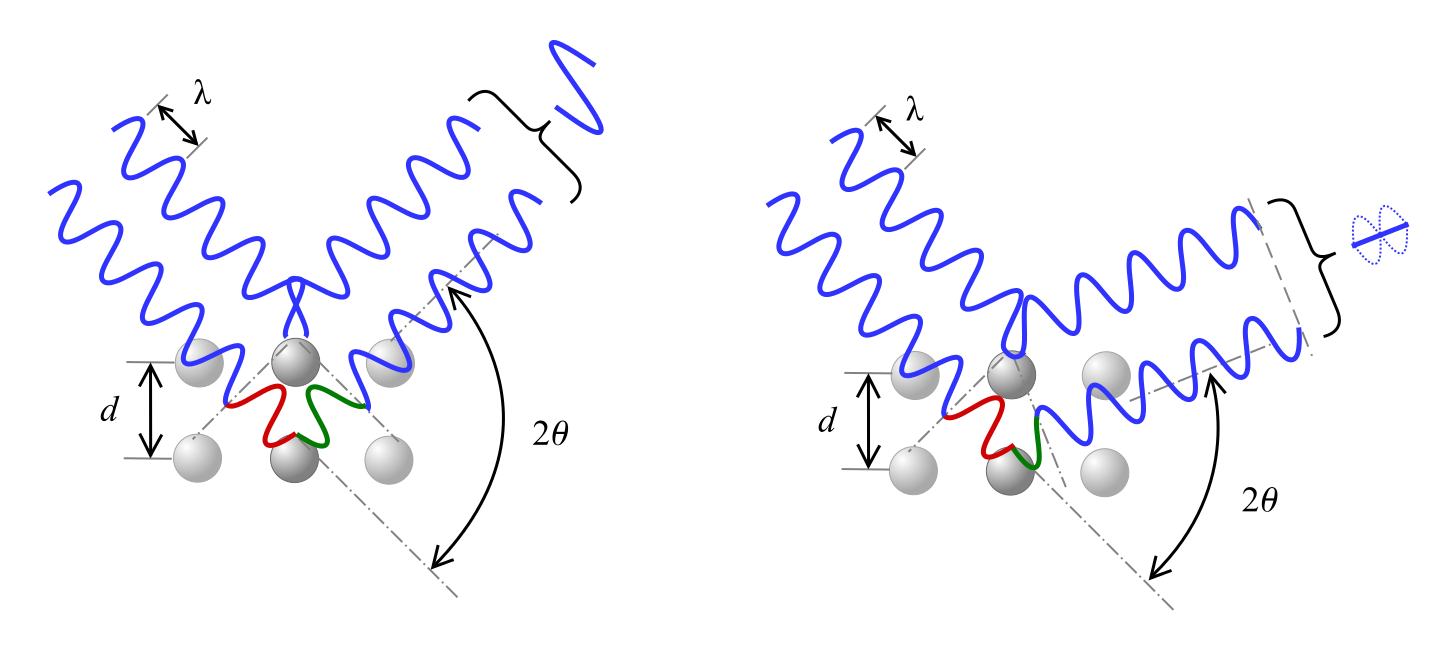
Sammenligninger til fortolkning af XRD-resultater
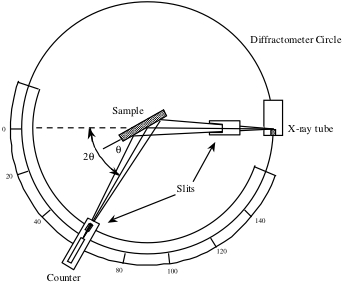
Tælleren, der ses nedenfor i en skematisk fremstilling af et røntgendiffraktometer, roteres over et område med 2θ-værdier og registrerer den røntgensignalintensitet, der reflekteres fra krystallen ved hver position. Denne intensitet målt som en funktion af 2θ bruges til at generere en peak-profil.
For vinkler, der opfylder Bragg-betingelsen, vil der blive observeret en peak i røntgensignalet på grund af den konstruktive interferens. Disse toppe bruges derefter til at identificere krystalretninger og beregne gitterparametre. For kubiske systemer kan den interplanare afstand, d, beregnes ved følgende ligning, der er afledt af krystalgeometrien, hvor a er gitterparameteren og h, k og l er Miller-indekserne.
Kombination af Braggs lov og den interplanare afstand giver følgende ligning.
Her har vi flyttet alle konstanterne til venstre side af ligningen, så vi kan sammenligne forholdet mellem sin2(θ)-værdier og Miller-indeks mellem forskellige toppe.
Når den indfaldende elektromagnetiske bølge rammer prøvematerialet, bliver elektroner, der befinder sig i materialet, forstyrret i et oscillerende mønster, som genererer nye røntgenstråler og effektivt spreder de indfaldende lysbølger. Der forekommer to typer af spredning: kohærent eller elastisk spredning omfatter tætbundne oscillerende elektroner, som spreder røntgenstråler med samme bølgelængde, og inkohærent spredning, som forekommer, når løstbundne elektroner sættes i svingende bevægelse og genererer røntgenstråler med forskellig energi. Røntgendiffraktion måler intensiteten af kohærent spredt røntgenstråling, som topper der, hvor bølgerne interfererer konstruktivt. Den atomare spredningsfaktor kan defineres som et forhold mellem amplituden af den bølge, der spredes af et atom, divideret med amplituden af den bølge, der spredes af en enkelt elektron. Dette forhold beskriver i det væsentlige et atoms spredningseffektivitet for en given retning.
Eksempel på XRD-data
Her er data indsamlet fra et eksperiment, som jeg lavede under mit bachelorlaboratoriekursus, hvor jeg forsøgte at identificere et ukendt metal ud fra dets krystalstruktur.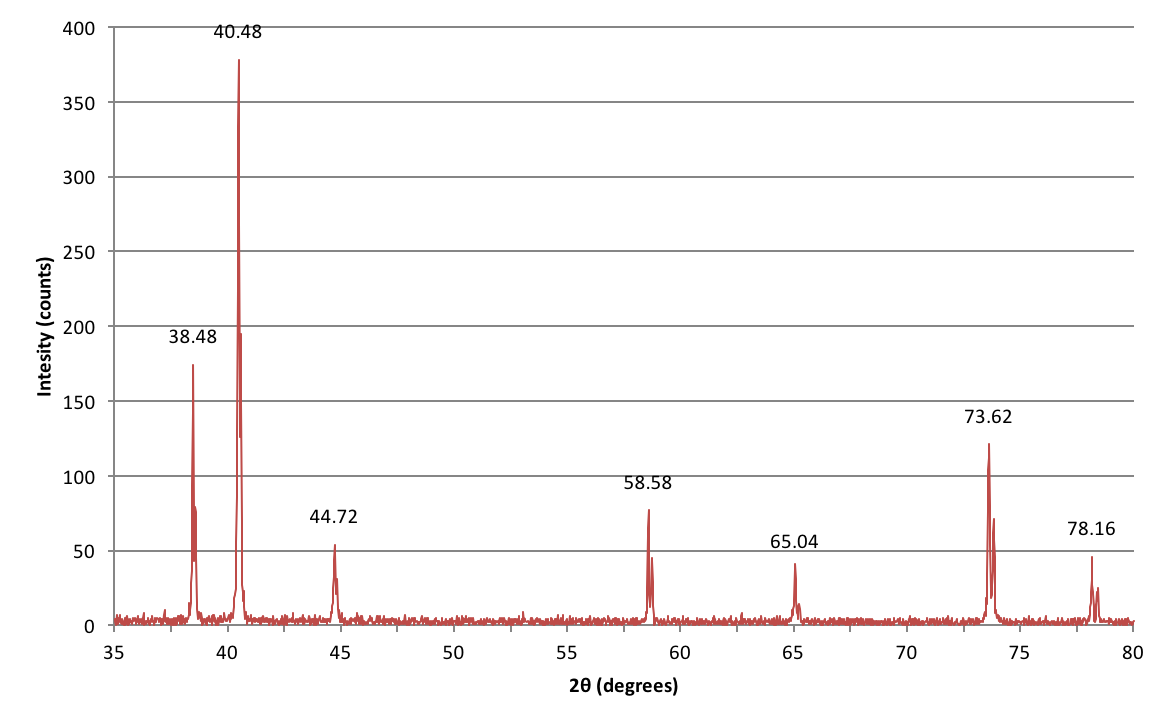
Hvordan skal jeg fortolke disse toppe?
| Krystalstruktur | Betingelser |
|---|---|
| Simple Cubic | alle h, k, l værdier |
| Body Centered Cubic | h+k+l skal være lige |
| Face Centered Cubic | h, k og l skal alle være ulige eller lige |
Strukturfaktorer tager højde for tilfælde, hvor et plan kan ligge halvvejs mellem to naboplaner, hvilket medfører destruktiv interferens. Disse faktorer resulterer i et sæt regler for forskellige krystalstrukturgeometrier, som bestemmer, hvornår konstruktiv interferens kan forekomme. Ovenstående tabel viser de Miller-indeks-parametre, hvor konstruktiv interferens vil forekomme. En mere omfattende tabel er vist nedenfor. Ved at sammenligne forholdet mellem sin2θ (betegnet som $Q^2$ i den anden tabel) for forskellige diffraktionstoppe kan krystalstrukturen og Miller-indekset bestemmes.
| Krystalplan (hkl) | $Q^2$ | Rumgitter, hvorfra refleksioner er mulige | ||||||
|---|---|---|---|---|---|---|---|---|
| 100 | 1 | SC | ||||||
| 110 | 2 | SC | BCC | |||||
| 111 | ||||||||
| 111 | 3 | SC | FCC | DC | ||||
| 200 | 4 | 4 | SC | BCC | FCC | |||
| 210 | 5 | SC | SC | |||||
| 211 | 6 | SC | BCC | |||||
| – | 7 | |||||||
| 220 | 8 | SC | BCC | FCC | DC | |||
| 300, 221 | 9 | SC | ||||||
| 310 | 10 | SC | BCC | |||||
| 311 | 11 | SC | FCC | DC | ||||
| 222 | 12 | SC | BCC | FCC | FCC | |||
| 320 | 13 | SC | ||||||
| 321 | 14 | SC | BCC | |||||
| 321 | – | 15 | ||||||
| 400 | 16 | SC | BCC | FCC | DC | |||
X-strålediffraktion har en lang række anvendelsesmuligheder til karakterisering af materialer. Den kan anvendes som en eksperimentel metode til eksperimentelt at bestemme volumenet af en enhedscelle med henblik på teoretiske tæthedsberegninger. Desuden vil det forvrængede gitter, hvis materialet er under restspænding, udvise en række d-afstande, der opfylder Braggs lov, hvilket resulterer i meget bredere diffraktionstoppe. Bredden af diffraktionstoppen kan også bruges til at bestemme partikelstørrelsen.