Quadratsignaler, også kaldet IQ-signaler, IQ-data eller IQ-prøver, anvendes ofte i RF-applikationer. De danner grundlaget for kompleks RF-signalmodulation og -demodulation, både i hardware og i software, samt i kompleks signalanalyse. Dette indlæg ser på begrebet IQ-signaler, og hvordan de anvendes.
Et par periodiske signaler siges at være i “kvadratur”, når de adskiller sig i fase med 90 grader. Det “i fase” eller referencesignal kaldes “I”, og det signal, der er forskudt med 90 grader (signalet i kvadratur), kaldes “Q”. Hvad betyder dette, og hvorfor er det vigtigt for os? Lad os bryde det ned ved at starte med nogle grundlæggende ting.
Grundlæggende om RF-modulation
Jeg vil starte med en gennemgang simpel RF-modulation. En umoduleret RF-bærer er simpelthen en sinusbølge som vist nedenfor.
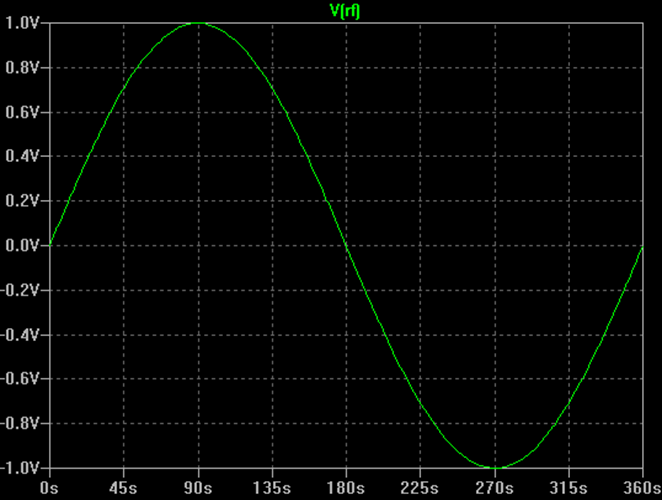
Signalet kan beskrives som en funktion af tiden ved følgende ligning:
V(t) = A * sin (2 * π * f * t * t + Ф)
hvor:
A: er spidsamplituden
f: er frekvensen
t: er tiden
Ф: er faseforskydningen
Information “transporteres” af en RF-bærer gennem en modulationsproces. Informationssignalet (tale, data osv.) bruges til at ændre egenskaberne ved RF-signalet. Et simpelt eksempel er Amplitudemodulation eller AM.
For AM bruges informationssignalet til at ændre eller modulere bæresignalets amplitude. Matematisk kan det repræsenteres ved at ændre konstanten “A” i den foregående ligning til et tidsvarierende signal (informationssignalet):
V(t) = A(t) * sin (2 * π * f * t + Ф)
Informationssignalet, også kendt som basisbåndssignalet, varierer meget langsommere med tiden end RF-signalet gør. For at se virkningen af modulationen skal man derfor observere RF-signalets envelope over en længere tidsskala, som vist nedenfor.
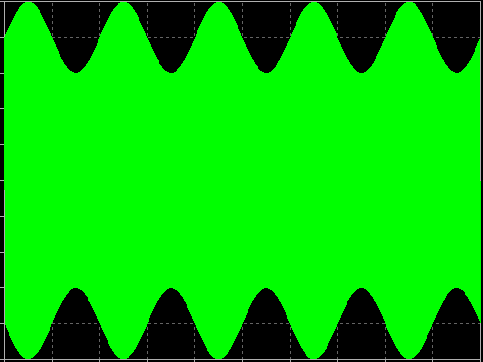
I dette tilfælde er A(t)-signalet en sinusform. Figuren viser, hvordan RF-signalets amplitude følger det sinusformede A(t)-basisbåndssignal.
Du kan udbygge dette ved at erkende, at andre egenskaber ved RF-bæreren kan ændres, eller moduleres, af et basisbåndssignal over tid. Hvis frekvensen moduleres af et basisbåndssignal, har man frekvensmodulation (FM). Hvis fasen moduleres på samme måde, er der tale om fasemodulation (PM). Således:
- A(t) er, når amplituden varieres mod tiden
- f(t) er, når frekvensen varieres mod tiden
- Ф(t) er, når fasen varieres mod tiden
- Ф(t) er, når fasen varieres mod tiden.
Hold det grundlæggende modulationsbegreb i tankerne, når vi knytter begrebet kvadratur-signaler til det…
Koncepter for kvadratur-signaler
Hvis faseforskellen Ф mellem to sinuskurver er 90 grader (eller π /2 radianer), siges disse to signaler at være i kvadratur. Et eksempel på dette er sinusbølgen og cosinusbølgen.
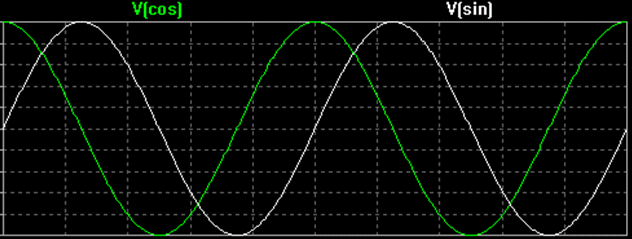
Som konvention er cosinusbølgen in-fase-komponenten, og sinusbølgen er kvadraturkomponenten. Det store bogstav I repræsenterer amplituden af in-fase-signalet, og det store bogstav Q repræsenterer amplituden af kvadratsignalet.
Udnyttelse af kvadratsignaler til modulering
Der sker interessante ting, når man ser på at lægge kvadratsignaler sammen.
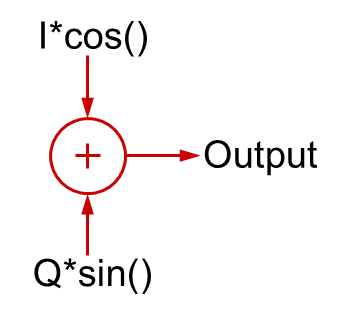
Hvis I=1 og Q=0, så ville man blot have cosinusbølgen (fase lig med 0). Tilsvarende ville man, hvis I=0 og Q=1, have sinusbølgen, som er det 90 grader forskudte signal.
Hvis både I og Q var lig med 1, vil summen være et nyt signal, som er vist grafisk nedenfor.
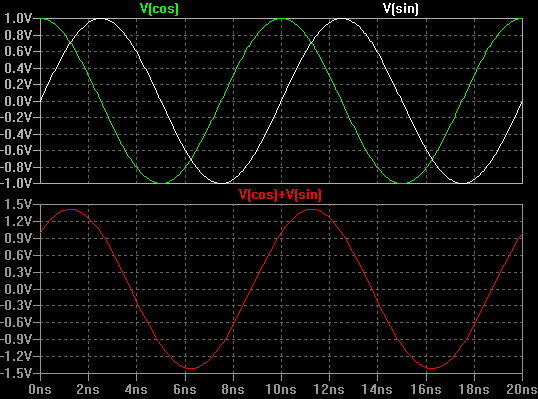
Bemærk, at hvis man lægger disse to kvadratsignaler med samme amplitude sammen, får man en ny sinuskurve, som er faseforskudt med 45 grader.
Nu kan du se, at amplituden og fasen af summen af kvadratur-signalerne er en funktion af værdien af I og Q. Derfor kan du skabe modulerede RF-signaler ved at variere I- og Q-værdierne i forhold til tiden. Lad os se på et par eksempler:
Digitale RF-modulationseksempler
Hvis Q=0, og I ændres mellem +1 og -1 over tid, skaber du et binært faseskiftet RF-signal (BPSK):
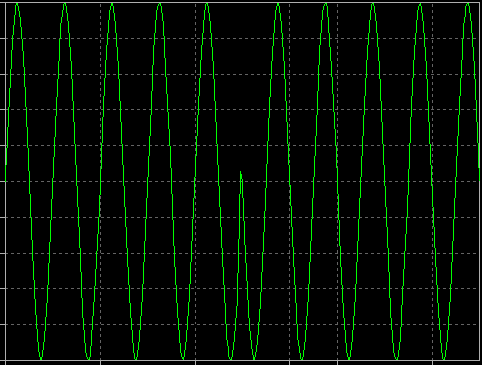
I(t)-signalet kunne være en simpel digital bitstrøm. Hvis du lader dette signal styre forstærkningen af RF-sinusoiden mellem +1 og -1, har du skabt et BPSK-signal.
Tager man dette et skridt videre … Hvis to digitale bits anvendes til at styre I- og Q-værdierne mellem +1 og -1 over tid, kan den resulterende sum af kvadratur-signalerne være en af fire forskellige faser:
- I=+1 & Q=+1 resulterer i en 45 graders fase
- I=-1 & Q=+1 resulterer i en 135 graders fase
- I=-1 & Q=-1 resulterer i 225 graders fase
- I=+1 & Q=-1 resulterer i 315 graders fase
Dette er kendt som QPSK-modulation (Quadrature Phase Shift Keying). Dette er to eksempler på kvadraturamplitudemodulation (QAM). De forskellige modulationstilstande for QAM er ofte vist på et konstellationsdiagram. Et konstellationsdiagram er simpelthen et fasordiagram, der viser et signals amplitude og fase som et polært plot.
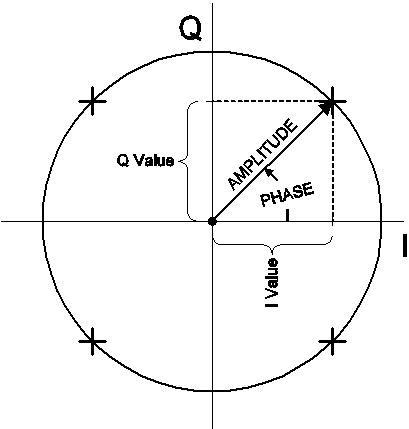
Vektorens længde fra oprindelsen repræsenterer signalets størrelse, og den vinkel, vektoren danner med den vandrette akse, repræsenterer fasen. De fire “tilstande” for det QPSK-signal, der er beskrevet ovenfor, er vist som de fire “+”-symboler i diagrammet. Du vil også bemærke, at den vandrette akse er mærket “I” og den lodrette akse er mærket “Q” – fordi disse repræsenterer de I- og Q-komponentværdier, der er forbundet med signalet.
Mere komplekse QAM-modulationer, som f.eks. 16QAM, har simpelthen flere tilstande. For 16QAM kan I- og Q-værdierne hver have en af fire diskrete værdier, hvilket giver 16 mulige kombinationer. Dette resulterer i 16 kombinationer af amplitude og fase for RF-signalet.
Kvadratursignaler overalt
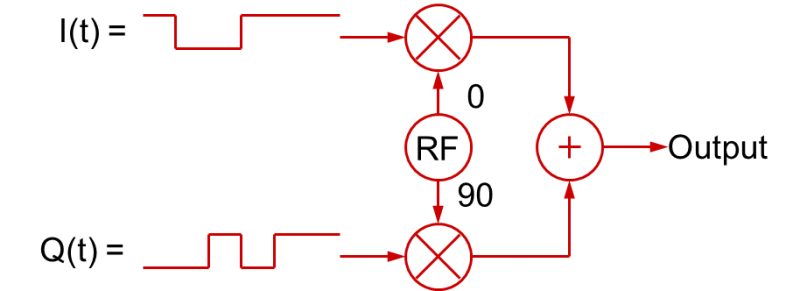
Anvendelse af I- og Q-signaler, der varierer over tid til at skabe modulerede RF-signaler, er ikke begrænset til digitale basisbåndssignaler. I(t)- og Q(t)-basisbåndssignalerne kan også være analoge basisbåndssignaler, og i de fleste “digitalt” modulerede RF-applikationer som QPSK eller nQAM filtreres basisbåndssignalerne faktisk for at bremse overgangene. Dette gøres for at begrænse den resulterende båndbredde af det modulerede RF-signal (hurtige digitale stignings- og faldtider optager en masse båndbredde!). Disse filtrerede digitale signaler er i realiteten analoge signaler! Så i mere generel forstand kan kvadraturmodulationsprocessen illustreres som vist i denne figur:
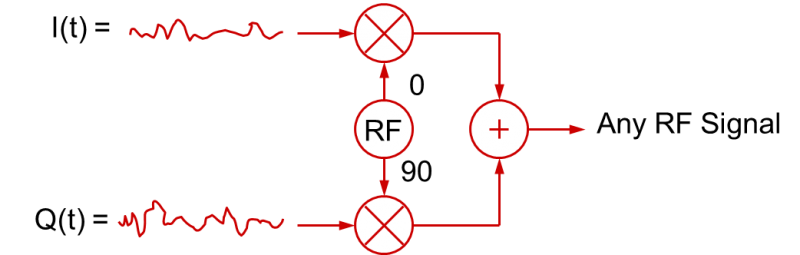
Den generelle konklusion, man kan drage af dette, er, at et RF-signal med en hvilken som helst type modulation kan skabes med de passende I(t) og Q(t) basisbåndssignaler (som igen varierer amplituderne af de cosinus- og sinusbølger, der summeres sammen).
Den samme proces fungerer naturligvis omvendt for at demodulere et RF-signal. Ved at blande et RF-signal med LO-signaler (lokaloscillator) i kvadratur kan der skabes I(t) og Q(t)-basisbåndssignaler.
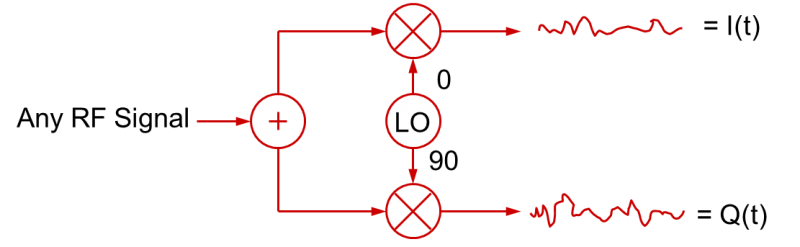
Dette er det grundlæggende grundlag for de fleste moderne RF-signalgenerering og -modulation samt demodulation og vektorsignalanalyse.
Software Defined Radio-systemer (SDR) anvender disse koncepter i vid udstrækning, fordi basisbånd I & Q-signalerne ofte repræsenteres som diskrete tidsafprøvede data. Derfor kan digital signalbehandling (DSP) anvendes til bogstaveligt talt at definere sender- og modtagerkarakteristika, herunder filtrering, modulation og demodulation, AGC osv. SDR-modtagere har ofte en basisbånd-båndbredde på et par hundrede kHz eller mere, hvilket giver mulighed for at udføre en lang række funktioner, herunder “brede” båndskue- og spektrogramfunktioner, samt at kunne overvåge og demodulere flere signaler af forskellige typer på én gang.
Vektorsignalgeneratorer har en kvadraturmodulator, der accepterer I(t)- og Q(t)-signaler, som den derefter bruger til at amplitudemodulere et par kvadratur-sinusoider, der derefter summeres for at skabe det modulerede RF-udgangssignal. Mange vektorsignalgeneratorer omfatter generelt paneludtag, hvor du kan tilslutte dine egne IQ-signaler. Mange omfatter en intern basisbånds Arbitrary Waveform Generator (AWG) til at skabe IQ-signalerne i basisbåndet.
Moderne Vektorsignalanalysatorer har typisk båndbredder på 25, 40, 110 MHz eller mere. De konverterer de indgående RF-signaler til deres I- og Q-komponenter. Alle analyser (spektralanalyse i forhold til tid, demodulation, impulsanalyse osv.) er blot forskellige matematiske behandlinger af de samme IQ-data. Real-Time Signal Analyzers, som f.eks. Tektronix RSA5000- og RSA6000-serierne, har den ekstra mulighed for at tage “live” IQ-datastrømme og udføre realtidsbehandling af dataene. Dette giver mulighed for at gøre ting som f.eks. at visualisere live-spektret af et RF-signal samt at kunne udløse transiente hændelser, som måske kun er synlige i frekvensdomænet.
Se Tektronix’ nyeste tilbud på spektrumanalysatorer.