Forudsætning – Grundlæggende grafteori – sæt 1
En graf er en struktur, der består af et sæt af objekter, hvor nogle par af objekterne på en eller anden måde er “relaterede”. Objekterne i grafen svarer til toppene, og relationerne mellem dem svarer til kanterne. En graf afbildes diagrammatisk som et sæt prikker, der afbilder toppunkter, forbundet af linjer eller kurver, der afbilder kanter.
Formelt set,
“En graf 
består af 
, et ikke-tomt sæt af toppunkter (eller knuder) og 
, et sæt af kanter. Hver kant har enten et eller to toppunkter tilknyttet, som kaldes dens endepunkter.”
Typer af grafer :Der findes flere typer af grafer, der skelnes på grundlag af kanter, deres retning, deres vægt osv.
1. Simpel graf – En graf, hvor hver kant forbinder to forskellige toppunkter, og hvor ingen to kanter forbinder det samme toppunktspar, kaldes en simpel graf. Betragt f.eks. følgende graf –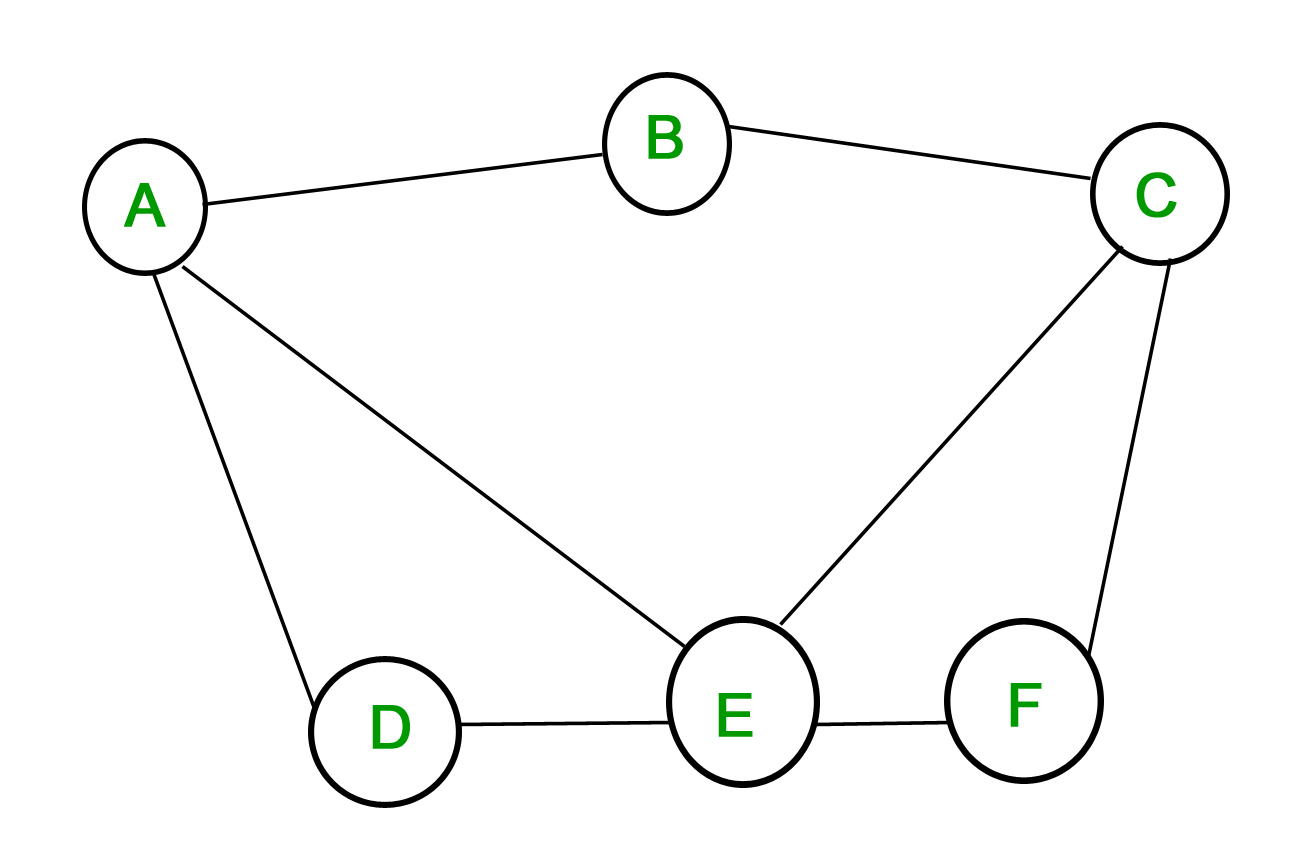
Overstående graf er en simpel graf, da intet toppunkt har en selvsløjfe, og ingen to toppunkter har mere end én kant, der forbinder dem.
Kanterne betegnes ved de toppunkter, de forbinder- 
er den kant, der forbinder toppunkterne 
og 
.
2. Multigraf – En graf, hvor flere kanter kan forbinde det samme toppunktspar, kaldes en multigraf.
Da der kan være flere kanter mellem det samme toppunktspar, fortæller mangfoldigheden af en kant antallet af kanter mellem to toppunkter.
Den ovenstående graf er en multigraf, da der er flere kanter mellem og 
. Multiplicitiviteten af kanten 
er 2.
I nogle grafer, i modsætning til den ovenfor viste, er kanterne retningsbestemte. Det betyder, at relationen mellem objekterne kun er envejs og ikke tovejs. Retningen af kanterne kan være vigtig i nogle anvendelser.
Baseret på, om kanterne er dirigerede eller ej, kan vi have dirigerede grafer og udirigerede grafer. Denne egenskab kan udvides til simple grafer og multigrafer for at få simple dirigerede eller udirigerede simple grafer og dirigerede eller udirigerede multigrafer.
Grundlæggende grafterminologi :
I ovenstående diskussion er der allerede blevet forklaret nogle termer vedrørende grafer som f.eks. hjørner, kanter, dirigerede og udirigerede kanter osv. Der er flere termer, som beskriver egenskaber ved hjørner og kanter.
- Adjacens – I en graf
siges to hjørner 
og 
at være tilstødende, hvis de er endepunkterne på en kant. Kanten 
siges at være tilstødende med toppene.
Hvis kanten er rettet, siges at være tilstødende til , og siges at være tilstødende fra . Her siges at være det indledende toppunkt, og siges at være det afsluttende toppunkt. - Grad – Graden af et toppunkt er antallet af kanter, der er sammenfaldende med det, bortset fra selvsløjfen, som bidrager to gange til toppunktets grad. Graden af et toppunkt betegnes som
.
I tilfælde af retningsbestemte grafer er graden yderligere klassificeret som in-degree og out-degree. Et toppunkts in-degree er antallet af kanter med det pågældende toppunkt som terminalpunkt. Et toppunkts out-degree er antallet af kanter med det givne toppunkt som begyndelsespunkt. In-degree angives som
og out-degree angives som 
.
For eksempel er in-degree for toppunktet “Delhi” i den ovenfor viste direkte graf, der viser flyvninger mellem byer, 3, og dets out-degree er også 3.
Bemærk: Hvis et toppunkt har en grad på nul, kaldes det isoleret. Hvis graden er én, kaldes den hængende.
Håndslags-sætning :
Hvad ville man få, hvis man lægger graderne for alle toppene i en graf sammen. I tilfælde af en udirigeret graf bidrager hver kant to gange, én gang for dens begyndelsesvertex og den anden for dens slutvertex. Så summen af grader er lig med det dobbelte af antallet af kanter. Denne kendsgerning er anført i Handshaking-sætningen.
Let be an undirected graph with edges. ThenIn case G is a directed graph,
Handshaking-sætningen, for udirigerede grafer, har et interessant resultat –
An undirected graph has an even number of vertices of odd degree.
Bevis : Lad 
og 
være mængderne af hjørner med henholdsvis lige og ulige grader.
Vi ved ved håndsætningen, at,
Så,
Summen af grader af toppunkter med lige grader er lige. LHS er også lige, hvilket betyder, at summen af grader af hjørner med ulige grader må være lige.
Dermed er antallet af hjørner med ulige grader lige.
Nogle specielle simple grafer :
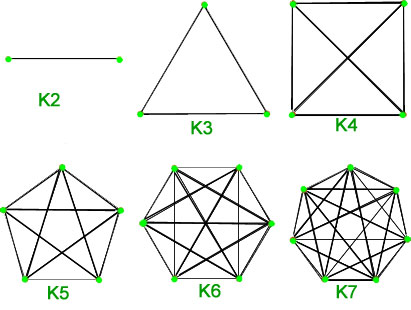
1. Komplette grafer – En simpel graf med 
toppunkter, der har præcis én kant mellem hvert par toppunkter, kaldes en komplet graf. En komplet graf med toppunkter betegnes med 
. Det samlede antal kanter er n*(n-1)/2 med n hjørner i en komplet graf.
2. Cyklusser – Cyklusser er simple grafer med hjørner 
og kanter 
. Cyklus med toppene betegnes som 
. Det samlede antal kanter er n med n toppunkter i cyklusgrafen.
3. Hjul – Et hjul er ligesom en cyklus med et ekstra toppunkt, som er forbundet med hvert andet toppunkt. Hjul med toppunkt med 1 tillægs toppunkt betegnes med 
. Det samlede antal kanter er 2*(n-1) med n hjørner i hjulgrafen.
4. Hypercube – Hypercube eller n-cube er en graf med 
hjørner, der hver især er repræsenteret ved en n-bit streng. De hjørner, der adskiller sig med højst 1 bit, er forbundet med kanter. En hypercube med hjørner betegnes med 
. Det samlede antal kanter er n*
med hjørner i kubens graf.
5. Bipartite grafer – En simpel graf siges at være bipartit, hvis dens toppunktsmængde kan opdeles i to disjunkte mængder, således at hver kant i har sit begyndelsespunkt i den første mængde og slutpunktet i den anden mængde. Det samlede antal kanter er (n*m) med (n+m) hjørner i en bipartit graf.
Sætning – En simpel graf er bipartit, hvis og kun hvis det er muligt at tildele en af to
forskellige farver til hvert hjørne i grafen, således at ingen to tilstødende hjørner tildeles den
samme farve.
En bipartit graf med 
og toppunkter i dens to disjunkte delmængder siges at være komplet, hvis der er en kant fra hvert toppunkt i den første mængde til hvert toppunkt i den anden mængde, i alt 
kanter. En komplet todelt graf med toppunkter i det første sæt og toppunkter i det andet sæt betegnes 
.
GATE CS Corner Questions
Du kan teste din viden ved at øve dig på de følgende spørgsmål. Alle spørgsmål er blevet stillet i GATE i tidligere år eller i GATE Mock Tests. Det anbefales på det kraftigste, at du øver dig i dem.
1. GATE CS 2013, spørgsmål 25
2. GATE CS 2014 Set-1, spørgsmål 61
3. GATE CS 2006, spørgsmål 71
4. GATE CS 2002, spørgsmål 25
5. GATE CS 2002, spørgsmål 25
5. GATE CS 2004, Spørgsmål 37
6. GATE CS 2014 Set-2, Spørgsmål 13
Referencer-
Graphs – Wikipedia
Discrete Mathematics and its Applications, af Kenneth H Rosen
Denne artikel er bidraget af Chirag Manwani. Hvis du kan lide GeeksforGeeks og gerne vil bidrage, kan du også skrive en artikel ved hjælp af contribute.geeksforgeeks.org eller sende din artikel på mail til [email protected]. Se din artikel blive vist på GeeksforGeeks’ hovedside, og hjælp andre nørder.