- Conectividade é um conceito básico da teoria dos gráficos. Ela define se um gráfico está conectado ou desconectado. Sem conectividade, não é possível atravessar um gráfico de um vértice para outro vértice.
- Diz-se que um gráfico está conectado se houver um caminho entre cada par de vértices. De cada vértice para qualquer outro vértice deve haver algum caminho a ser percorrido. Isto é chamado de conectividade de um gráfico.
- Diz-se que um gráfico é desconectado, se houver múltiplos vértices e bordas desconectados.
- Teorias de conectividade de gráficos são essenciais em aplicações de rede, redes de transporte de roteamento, tolerância de rede etc.
Exemplo
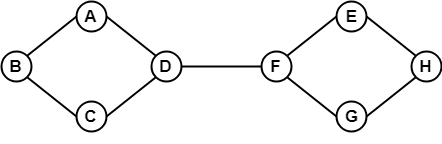
No exemplo acima, é possível viajar de um vértice para outro vértice. Aqui, podemos atravessar do vértice B para H usando o caminho B -> A -> D -> F -> E -> H. Assim, é um gráfico conectado.
Exemplo
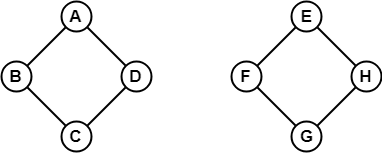
No exemplo acima, não é possível atravessar do vértice B para H porque não há caminho entre eles direta ou indiretamente. Portanto, é um gráfico desconectado.
Vejamos alguns conceitos básicos de Conectividade.
Vértice Corte
Um único vértice cuja remoção desconecta um gráfico é chamado de vértice corte.
Deixe G ser um gráfico conectado. Um vértice v de G é chamado de vértice cortado de G, se G-v (Remove v de G) resultar em um gráfico desconectado.
Quando removemos um vértice de um gráfico então o gráfico irá quebrar em dois ou mais gráficos. Este vértice é chamado de vértice de corte.
Nota: Deixe G ser um gráfico com n vértices:
- Um gráfico G conectado pode ter no máximo (n-2) vértices de corte.
- Remover um vértice de corte pode deixar um gráfico desconectado.
- Remover um vértice pode aumentar o número de componentes em um gráfico em pelo menos um.
- Todo o vértice não-cortado de uma árvore é um vértice cortado.
Exemplo 1

Exemplo 2
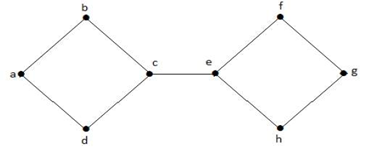
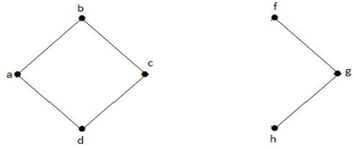
No gráfico acima, o vértice ‘e’ é um vértice cortado. Após remover o vértice ‘e’ do gráfico acima, o gráfico se tornará um gráfico desconectado.
Cut Edge (Bridge)
A cut- Edge ou bridge é uma única borda cuja remoção desconecta um gráfico.
Let G ser um gráfico conectado. Uma borda e de G é chamada de borda cortada de G, se G-e (Remove e de G) resultar em um gráfico desconectado.
Quando removemos uma aresta de um gráfico, então o gráfico irá quebrar em dois ou mais gráficos. Esta remoção de borda é chamada de aresta cortada ou ponte.
Nota: Deixe G ser um gráfico com n vértices:
- Um gráfico G conectado pode ter no máximo (n-1) arestas cortadas.
- Remover uma aresta cortada pode deixar um gráfico desconectado.
- Remover uma aresta pode aumentar o número de componentes em um gráfico no máximo em um.
- Uma aresta cortada ‘e’ não deve ser a parte de qualquer ciclo em G.
- Se uma aresta cortada existe, então um vértice cortado também deve existir porque pelo menos um vértice de uma aresta cortada é um vértice cortado.
- Se um vértice de corte existe, então a existência de qualquer aresta cortada não é necessária.
Exemplo 1
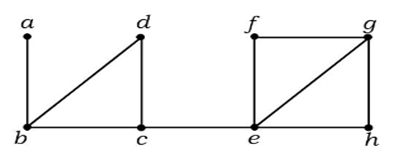
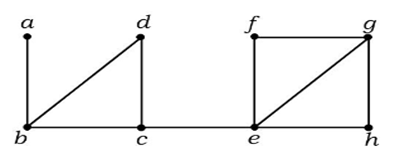
No gráfico acima, aresta (c, e) é uma aresta cortada. Após remover esta borda do gráfico acima, o gráfico tornar-se-á um gráfico desconectado.
Exemplo 2
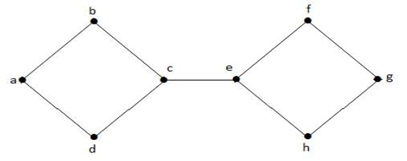
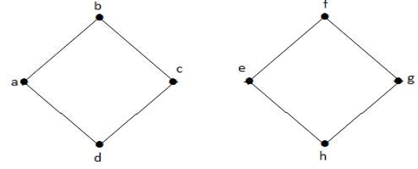
No gráfico acima, a borda (c, e) é uma borda cortada. Após remover esta aresta do gráfico acima, o gráfico se tornará um gráfico desconectado.
Cut Set
Em um gráfico G conectado, um conjunto de corte é um conjunto S de arestas com as seguintes propriedades:
- A remoção de todas as arestas em S desconecta G.
- A remoção de algumas das arestas (mas não todas) em S não desconecta G.
Exemplo 1
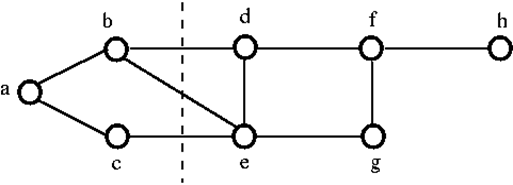
Para desconectar o gráfico G acima, temos que remover as três arestas, ou seja, bd, be e ce. Não podemos desconectá-lo removendo apenas duas das três arestas. Assim, {bd, be, ce} é um conjunto de corte.
Após remover o conjunto de corte do gráfico acima, pareceria como se segue:
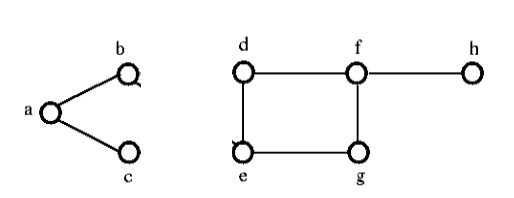
Edge Connectivity
A conectividade da borda de um gráfico G conectado é o número mínimo de arestas cuja remoção faz G desconectado. É denotado por λ(G).
Quando λ(G) ≥ k, então o gráfico G é dito como sendo k-edge-connected.
Exemplo
Vejamos um exemplo,
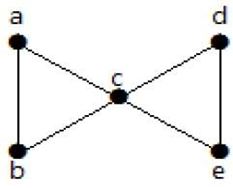
Do gráfico acima, ao remover duas arestas mínimas, o gráfico conectado torna-se gráfico desconectado. Portanto, sua conectividade de borda é 2. Portanto, o gráfico acima é um gráfico com 2 bordas conectadas.
Aqui estão as seguintes quatro formas de desconectar o gráfico removendo duas bordas:
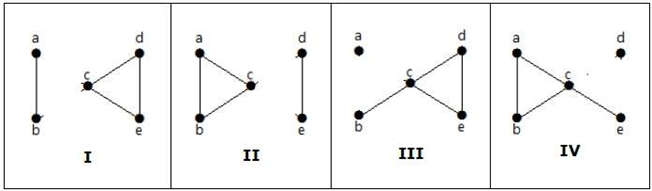
Conectividade de vértices
A conectividade (ou conectividade de vértices) de um gráfico G conectado é o número mínimo de vértices cuja remoção faz com que G desconecte ou reduza para um gráfico trivial. Ele é denotado por K(G).
O gráfico é dito para ser k- conectado ou k-vertex conectado quando K(G) ≥ k. Para remover um vértice nós também devemos remover as bordas incidentes a ele.
Exemplo
Vejamos um exemplo:
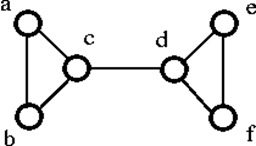
O gráfico G acima pode ser desconectado pela remoção do vértice único ou ‘c’ ou ‘d’. Portanto, sua conectividade de vértice é 1. Portanto, é um gráfico 1-conectado.