Cinética Química
Cinética Química
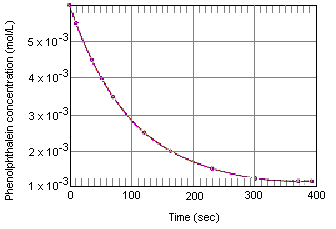
Você pode estar familiarizado com titulações ácido-base que usam fenolftaleína como indicador do ponto final. Você pode não ter notado, no entanto, o que acontece quando uma solução que contém fenolftaleína na presença de excesso de base é permitida por alguns minutos. Embora a solução tenha inicialmente uma cor rosada, a fenolftaleína vai-se tornando gradualmente incolor com o íon OH numa solução fortemente básica.
A tabela abaixo mostra o que acontece com a concentração de fenolftaleína numa solução que inicialmente estava 0,005 M em fenolftaleína e 0,61 M em OH-ion. Como você pode ver quando estes dados são plotados no gráfico abaixo, a concentração de fenolftaleína diminui por um fator de 10 ao longo de um período de cerca de quatro minutos.
Dados experimentais para a reacção entre a fenolftaleína e o excesso de base
Experimentos como o que nos deu os dados da tabela acima são classificados como medidas de cinética química (de um caule grego que significa “tomove”). Um dos objetivos destes experimentos é descrever a taxa de reação – a taxa na qual os reagentes são transformados nos produtos da reação.
O termo taxa é freqüentemente usado para descrever a mudança em uma quantidade que ocorre por unidade de tempo. A taxa de inflação, por exemplo, é a variação no custo médio de uma coleção de itens padrão por ano. A taxa na qual um objeto atravessa o espaço é a distância percorrida por unidade de tempo, tal como milhas por hora ou quilômetros por segundo. Na cinética química, a distância percorrida é a mudança na concentração de um dos componentes da reação. A taxa de uma reação é, portanto, a mudança na concentração de um dos reagentes![]() (X)
(X)![]() que ocorre durante um determinado período de tempo
que ocorre durante um determinado período de tempo![]() t.
t.
![]()
Problema de prática 1:
Utilizar os dados da tabela acima para calcular a taxa de reação da fenolftaleína com o íon OH durante cada um dos períodos seguintes:
(a) Durante o primeiro intervalo de tempo, quando a concentração de fenolftaleína cai de 0,0050 M para 0,0045 M.
(b) Durante o segundo intervalo, quando a concentração cai de 0,0045 M para 0,0040 M.
(c) Durante o terceiro intervalo, quando a concentração cai de 0,0040 M para 0,0035 M.
Clique aqui para verificar a sua resposta ao Problema de Prática 1.
Clique aqui para ver a solução do Problema de Prática 1.
![]()
Taxas de Reação Instantâneas e a Lei de Taxa de Reação
A taxa de reação entre a fenolftaleína e o OH-ion não é constante; ela muda com o tempo. Como a maioria das reações, a taxa desta reação diminui gradativamente à medida que os reagentes são consumidos. Isto significa que a taxa de reação muda enquanto está sendo medida.
Para minimizar o erro que isto introduz nas nossas medições, parece aconselhável medir a taxa de reacção ao longo de períodos de tempo que são curtos em comparação com o tempo que leva para que a reacção ocorra. Podemos tentar, por exemplo, medir a alteração infinitesimalmente pequena na concentração![]() d(X)
d(X)![]() que ocorre durante um período de tempo infinitesimalmente curto. A razão dessas quantidades é conhecida como a taxa instantânea de reação.
que ocorre durante um período de tempo infinitesimalmente curto. A razão dessas quantidades é conhecida como a taxa instantânea de reação.
![]()
A taxa instantânea de reação em qualquer momento no tempo pode ser calculada a partir de um gráfico da concentração do reagente (ou produto) versus tempo. O gráfico abaixo mostra como a taxa de reação para a decomposição da fenolftaleína pode ser calculada a partir de um gráfico de concentração versus tempo. A taxa de reação em qualquer momento no tempo é igual à inclinação de uma tangente traçada a esta curva naquele momento.
![]()
Lei e Constantes de Taxa
Um resultado interessante é obtido quando a taxa instantânea de reação é calculada em vários pontos ao longo da curva no gráfico da seção anterior. A taxa de reação em cada ponto desta curva é diretamente proporcional à concentração de fenolftaleína naquele momento no tempo.
Rate = k(fenolphthalein)
Porque esta equação é uma lei experimental que descreve a taxa da reação, ela é chamada de lei de taxa para a reação. A constante proporcionalityconstant, k, é conhecida como constante de taxa.
Practice Problem 2:
Calcule a constante de taxa para a reação entre a fenolftaleína e o íon OH se a taxa instantânea de reação for 2,5 x 10-5 mole por litro por segundo quando a concentração de fenolftaleína for 0,0025 M.
Clique aqui para verificar sua resposta ao Practice Problem 2.
Clique aqui para ver uma solução ao Practice Problem 2.
Problema de Prática 3:
Utilize a constante de taxa de reacção entre a fenolftaleína e o ião OH para calcular a taxa instantânea inicial de reacção para os dados experimentais listados na tabela anterior.
Clique aqui para verificar a sua resposta ao Problema da Prática 3.
Clique aqui para ver uma solução ao Problema da Prática 3.
![]()
Diferentes formas de expressar a Taxa de Reacção
Existe normalmente mais do que uma forma de medir a taxa de uma reacção. Wecan estuda a decomposição do iodeto de hidrogênio, por exemplo, medindo a taxa na qual ou H2 ou I2 é formado na seguinte reação ou therate na qual HI é consumido.
2 HI(g) H2(g) + I2(g)
Experimentalmente encontramos que a taxa na qual I2 é formado é proporcional ao quadrado da concentração de HI em qualquer momento no tempo.
>![]()
O que aconteceria se estudássemos a taxa de formação do H2? A equação equilibrada sugere que H2 e I2 devem ser formados exatamente na mesma taxa.
![]()
O que aconteceria, entretanto, se estudássemos a taxa de consumo do HI nesta reação? Como o HI é consumido, a mudança na sua concentração deve ser um número anegativo. Por convenção, a taxa de uma reação é sempre relatada como um número positivo. Portanto, temos que mudar o sinal antes de reportar a taxa de reação para o areactante que é consumido na reação.
![]()
O sinal negativo faz duas coisas. Matematicamente, ele converte uma variação negativa na concentração de HI em uma taxa positiva. Fisicamente, lembra-nos que a concentração do reagente diminui com o tempo.
Qual é a relação entre a taxa de reacção obtida bymonitorizando a formação de H2 ou I2 e a taxa obtida ao observar o HI desaparecer? A estequiometria da reação diz que duas moléculas de HI são consumidas para cada molécula de H2 ou I2 produzida. Isto significa que a taxa de decomposição do HI é duas vezes mais rápida do que a taxa na qual H2 e I2 são formados. Podemos traduzir esta relação em uma equação matemática da seguinte forma.
![]()
Como resultado, a constante de taxa obtida pelo estudo da taxa a que H2 e I2 são formados nesta reação (k) não é a mesma constante de taxa obtida pelo monitoramento da taxa a que HI é consumido (k’)
Problema da prática 4:
Calcular a taxa a que HI desaparece na reação seguinte no momento em que I2 está sendo formado a uma taxa de 1.8 x 10-6 moles por litro por segundo:
2 HI(g) ![]() H2(g) + I2(g)
H2(g) + I2(g)
Clique aqui para verificar a sua resposta ao Problema da Prática 4.
Clique aqui para ver uma solução para o Problema da Prática 4.
![]()
A Lei da Taxa versus a Estequiometria da Reacção
Nos anos 30, Sir Christopher Ingold e colegas de trabalho da Universidade de Londres estudaram a cinética das reacções de substituição, tais como
CH3Br(aq) + OH-(aq)
CH3OH(aq) + Br-(aq)
Verificaram que a taxa desta reacção é proporcional às concentrações de ambos os reagentes.
Taxa = k(CH3Br)(OH-)
Quando eles executaram uma reação semelhante em um material de arranque ligeiramente diferente, eles obtiveram produtos semelhantes.
(CH3)3CBr(aq) + OH-(aq)![]() (CH3)3COH(aq) + Br-(aq)
(CH3)3COH(aq) + Br-(aq)
Mas agora a taxa de reação era proporcional à concentração de apenas um dos reagentes.
Taxa = k((CH3)3CBr)
Estes resultados ilustram um ponto importante: A lei da taxa de areação não pode ser prevista a partir da estequiometria da reação; ela deve ser determinada experimentalmente. Às vezes, a lei de taxas é consistente com o que se espera da estequiometria da reação.
2 HI(g) H2(g) + I2(g)
Taxa = k(HI)2
Amaciar, no entanto, não é.
| 2 N2O5(g) |
Taxa = k(N2O5) |
![]()
Ordem de Molecularidade
Algumas reacções ocorrem num único passo. A reação na qual uma clorineatom é transferida de ClNO2 para NO para formar NO2 e ClNO é um bom exemplo de uma reação de um passo.
ClNO2(g) + NO(g)
NO2(g) + ClNO(g)
Outras reações ocorrem por uma série de passos individuais. N2O5, por exemplo, decompõe-se em NO2 e O2 através de um mecanismo de três passos.
| Passo 1: | N2O5 |
|
| Passo 2: | NO2 + NO3 |
|
| Passo 3: | NO + NO3 |
Os passos de uma reacção são classificados em termos de molecularidade, que descreve o número de moléculas consumidas. Quando uma única molécula é consumida, a etapa é chamada unimolecular. Quando duas moléculas são consumidas, ela é bimolecular.
Problema de Prática 5.
Determine a molecularidade de cada passo da reacção pela qual N2O5 se decompõe em NO2 e O2.
Clique aqui para verificar a sua resposta ao Problema de Prática 5.
Clique aqui para ver uma solução ao Problema de Prática 5.
Reacções também podem ser classificadas em termos da sua ordem. A decomposição de N2O5 é uma reação de primeira ordem porque a taxa de reação depende da concentração de N2O5 elevada à primeira potência.
Taxa = k(N2O5)
A decomposição de HI é uma reação de segunda ordem porque a taxa de reação depende da concentração de HI elevada à segunda potência.
Taxa = k(HI)2
Quando a taxa de uma reacção depende mais do que de um reagente, classificamos a reacção em termos da ordem de cada reagente.
Problema de Prática 6:
Classificar a ordem da reação entre NO e O2 para formar NO2:
2 NO(g) + O2(g) ![]() 2 NO2(g)
2 NO2(g)
Classificar a seguinte lei de taxa para esta reação:
Classificar = k(NO)2(O2)
>Clique aqui para verificar a sua resposta ao Problema de Prática 6.
A diferença entre a molecularidade e a ordem de uma reação é importante. A molecularidade de uma reação, ou um passo dentro de uma reação, descreve o que acontece no nível molecular. A ordem de uma reação descreve o que acontece na escala macroscópica. Nós determinamos a ordem de uma reação observando o aparecimento dos produtos de uma reação ou o desaparecimento dos reagentes. A molecularidade da reação é algo que deduzimos para explicar estes resultados experimentais.
![]()
Modelo Teórico de Reações Químicas
O modelo teórico de colisão de reações químicas pode ser usado para explicar as leis de taxa observadas tanto para reações de um passo quanto para reações de múltiplos passos. Este modelo pressupõe que a taxa de qualquer etapa de uma reação depende da freqüência de colisão entre as partículas envolvidas naquela etapa.
A figura abaixo fornece uma base para entender as implicações do modelo da teoria de colisão para reações simples de uma etapa, tais como as seguintes.
ClNO2(g) + NO(g) ![]() NO2(g) + ClNO(g)
NO2(g) + ClNO(g)
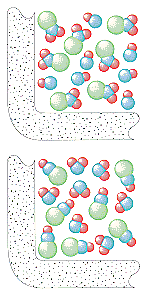
A teoria molecular cinética assume que o número de colisões perseguidas num gás depende do número de partículas por litro. A taxa de formação de NO2e ClNO nesta reação deve, portanto, ser diretamente proporcional às concentrações de ClNO2e NO.
Taxa = k(ClNO2)(NO)
O modelo da teoria da colisão sugere que a taxa de qualquer etapa da reação é proporcional às concentrações dos reagentes consumidos nessa etapa. A lei tera para uma reação em um passo deve, portanto, concordar com a estequiometria da reação.
A reação seguinte, por exemplo, ocorre em um único passo.
CH3Br(aq) + OH-(aq) ![]() CH3OH(aq) + Br-(aq)
CH3OH(aq) + Br-(aq)
Quando estas moléculas colidem na orientação apropriada, um par de elétrons não ligados no íon OH- pode ser doado ao átomo de carbono no centro da molécula CH3Br, como mostrado na figura abaixo.
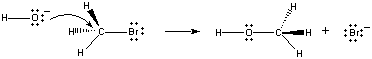
Quando isto acontece, uma ligação carbono-oxigénio forma-se ao mesmo tempo em que a ligação carbono-bromo é quebrada. O resultado líquido desta reação é a substituição do íon anOH-ion por um íon Br – ion. Como a reação ocorre em uma estepe singlética, que envolve colisões entre os dois reagentes, a taxa desta reação é proporcional à concentração dos dois reagentes.
Rate = k(CH3Br)(OH-)
Nada todas as reações ocorrem em uma única etapa. A reação seguinte ocorre em três passos, como mostrado na figura abaixo.
(CH3)3CBr(aq) + OH-(aq)![]() (CH3)3COH(aq) + Br-(aq)
(CH3)3COH(aq) + Br-(aq)
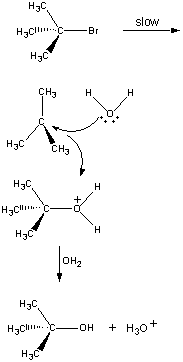
No primeiro passo, o (CH3)3CBr moleculedissocia-se em um par de íons.
| Primeiro passo | 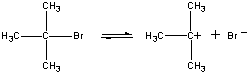 |
O íon (CH3)3C+ positivamente carregado reage com água em um segundo passo.
| Segundo passo | 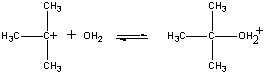 |
O produto desta reacção perde então um próton para o ião OH ou água no passo final.
| Terceiro passo | 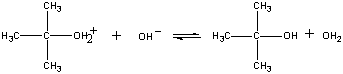 |
Os segundo e terceiro passos desta reacção são muito mais rápidos que o primeiro.
| (CH3)3CBr |
Passo baixo | |
| (CH3)3C+ + H2O |
Passo rápido | |
| (CH3)3COH2+ + OH- |
Passos rápidos |
A taxa global de reacção é portanto mais ou menos igual à taxa do primeiro passo. O primeiro passo é, portanto, chamado passo limitador da taxa desta reação porque limita literalmente a taxa na qual os produtos da reação podem ser formados. Como apenas um reagente está envolvido na etapa limitadora da taxa, a taxa global da reacção é proporcional à concentração apenas deste reagente.
Taxa = k((CH3)3CBr)
A lei da taxa para esta reacção difere, portanto, do que nós prevíamos da estequiometria da reacção. Embora a reacção consuma ambos (CH3)3CBrand OH-, a taxa da reacção é apenas proporcional à concentração de(CH3)3CBr.
As leis de taxa para reacções químicas podem ser explicadas pelas seguintes regras gerais.
A taxa de qualquer etapa de uma reacção é directamente proporcional às concentrações dos reagentes consumidos nessa etapa.
A lei de taxa global para uma reacção é determinada pela sequência de passos, ou o mecanismo, pelo qual os reagentes são convertidos nos produtos da reacção.
A lei de taxa global para uma reacção é dominada pela lei de taxa para o passo mais lento da reacção.