Classificação por análise discriminante
Vejamos como a LDA pode ser derivada como um método de classificação supervisionado. Considere um problema de classificação genérico: Uma variável aleatória X vem de uma das classes K, com algumas densidades de probabilidade f(x) específicas da classe. Uma regra discriminante tenta dividir o espaço de dados em regiões de K disjoint que representam todas as classes (imagine as caixas em um tabuleiro de xadrez). Com essas regiões, a classificação por análise discriminante significa simplesmente que alocamos x à classe j se x estiver na região j. A questão é, então, como saber em que região os dados x se encaixam? Naturalmente, podemos seguir duas regras de alocação:
- Regra de máxima probabilidade: Se assumirmos que cada classe pode ocorrer com igual probabilidade, então alocar x para a classe j if
- Regra Bayesiana: Se conhecemos as probabilidades anteriores da classe, π, então alocar x para a classe j if

Análise discriminante linear e quadrática
Se assumirmos que os dados provêm da distribuição multivariada gaussiana, i.e. a distribuição de X pode ser caracterizada pela sua média (μ) e covariância (Σ), formas explícitas das regras de alocação acima podem ser obtidas. Seguindo a regra Bayesiana, classificamos os dados x para a classe j se ela tiver a maior probabilidade entre todas as classes de K para i = 1,…,K:

A função acima é chamada de função discriminante. Note aqui o uso de log-likelihood. Em outra palavra, a função discriminante nos diz quão prováveis os dados x são de cada classe. O limite de decisão que separa quaisquer duas classes, k e l, portanto, é o conjunto de x onde duas funções discriminantes têm o mesmo valor. Portanto, qualquer dado que cai no limite de decisão é igualmente provável a partir das duas classes (não conseguimos decidir).
LDA surge no caso em que assumimos igual covariância entre as classes K. Isto é, ao invés de uma matriz de covariância por classe, todas as classes têm a mesma matriz de covariância. Então podemos obter a seguinte função discriminante:

Notem que esta é uma função linear em x. Assim, a fronteira de decisão entre qualquer par de classes é também uma função linear em x, a razão de seu nome: análise linear discriminante. Sem a hipótese de igual covariância, o termo quadrático na probabilidade não se cancela, portanto a função discriminante resultante é uma função quadrática em x:

Neste caso, o limite de decisão é quadrático em x. Isto é conhecido como análise discriminante quadrática (QDA).
O que é melhor? LDA ou QDA?
Em problemas reais, os parâmetros populacionais são geralmente desconhecidos e estimados a partir dos dados de treinamento como a média da amostra e as matrizes de covariância da amostra. Enquanto o QDA acomoda limites de decisão mais flexíveis em comparação com o LDA, o número de parâmetros necessários para ser estimado também aumenta mais rapidamente do que o LDA. Para LDA, (p+1) são necessários parâmetros para construir a função discriminante em (2). Para um problema com classes K, precisaríamos apenas (K-1) dessas funções discriminantes, escolhendo arbitrariamente uma classe para ser a classe base (subtraindo a probabilidade da classe base de todas as outras classes). Assim, o número total de parâmetros estimados para LDA é (K-1)(p+1).
Por outro lado, para cada função QDA discriminante em (3), vetor médio, matriz de covariância e classe anterior precisam ser estimados:
– Média: p
– Covariância: p(p+1)/2
– Classe prior: 1
Simplesmente, para QDA, precisamos estimar parâmetros (K-1){p(p+3)/2+1}.
Por isso, o número de parâmetros estimados no LDA aumenta linearmente com p enquanto que o do QDA aumenta quadraticamente com p. Esperávamos que o QDA tivesse pior desempenho que o LDA quando a dimensão do problema é grande.
Melhor de dois mundos? Compromisso entre LDA & QDA
Podemos encontrar um compromisso entre LDA e QDA ao regularizar as matrizes de covariância de classe individual. Regularização significa que nós colocamos uma certa restrição nos parâmetros estimados. Neste caso, exigimos que a matriz de covariância individual encolha para uma matriz de covariância comum através de um parâmetro de penalidade, por exemplo, α:

A matriz de covariância comum também pode ser regularizada para uma matriz de identidade através de um parâmetro de penalidade, por exemplo β:

>>
>
Em situações em que o número de variáveis de entrada excede em muito o número de amostras, a matriz de covariância pode ser mal estimada. A retração pode, espera-se, melhorar a estimativa e a precisão da classificação. Isto é ilustrado pela figura abaixo.

Computação para LDA
Vemos em (2) e (3) que os cálculos de funções discriminantes podem ser simplificados se diagonalizarmos primeiro as matrizes de covariância. Ou seja, os dados são transformados para ter uma matriz de covariância de identidade (sem correlação, variância de 1). No caso da LDA, eis como procedemos com o cálculo:

Passo 2 esferece os dados para produzir uma matriz de covariância de identidade no espaço transformado. O passo 4 é obtido seguindo (2).
Vamos dar um exemplo de duas classes para ver o que a LDA está realmente fazendo. Suponha que existem duas classes, k e l. Nós classificamos x para a classe k se

A condição acima significa que a classe k tem mais probabilidade de produzir dados x do que a classe l. Seguindo os quatro passos descritos acima, escrevemos
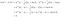
Isto é, classificamos os dados x à classe k se

A regra de alocação derivada revela o funcionamento da LDA. O lado esquerdo (s.l.h.) da equação é o comprimento da projeção ortogonal de x* no segmento de linha que une as duas médias de classe. O lado direito é a localização do centro do segmento corrigido por probabilidades prévias de classe. Essencialmente, o LDA classifica os dados esféricos para a média de classe mais próxima. Podemos fazer duas observações aqui:
- O ponto de decisão se desvia do ponto médio quando as probabilidades anteriores da classe não são as mesmas, ou seja, o limite é empurrado para a classe com uma probabilidade anterior menor.
- Os dados são projetados no espaço delimitado pelas médias da classe (a multiplicação de x* e a subtração da média no s.l.h. da regra). Comparações de distância são então feitas nesse espaço.