La difracción de rayos X es una técnica común de caracterización de materiales que permite identificar las orientaciones de los cristales y el espaciado interatómico. Los rayos X se utilizan para esto porque la longitud de onda está en la misma escala de longitud que los valores de los parámetros de espaciamiento interatómico y de red.
¿Qué sucede?
Un rayo X se genera en un tubo de vacío calentando un filamento de tungsteno más allá de su función de trabajo para expulsar electrones. Las condiciones de vacío son necesarias para aumentar el recorrido libre medio de los electrones. Los electrones se aceleran en un cátodo de cobre con una energía del orden de 25 keV. Las colisiones de los electrones con el cátodo de cobre dan lugar a ionizaciones de la capa interna, produciendo rayos X a medida que los electrones de mayor energía caen para llenar la vacante de menor energía. Los electrones de varios niveles de energía más altos caen, produciendo ondas electromagnéticas de energía variable. Así, se generan rayos X de múltiples longitudes de onda (de tipo K-beta y K-alfa). Para la difracción de rayos X, lo ideal es tener luz monocromática que interactúe con la muestra, por lo que los rayos X K-beta se filtran con una placa de níquel. Aunque efectivamente hay dos energías K-alfa asociadas, las energías son tan similares que no afecta significativamente al perfil general del pico. Los rayos X pasan a través de un colimador para ajustar la anchura del haz.
Un poco de antecedentes con la ley de Bragg
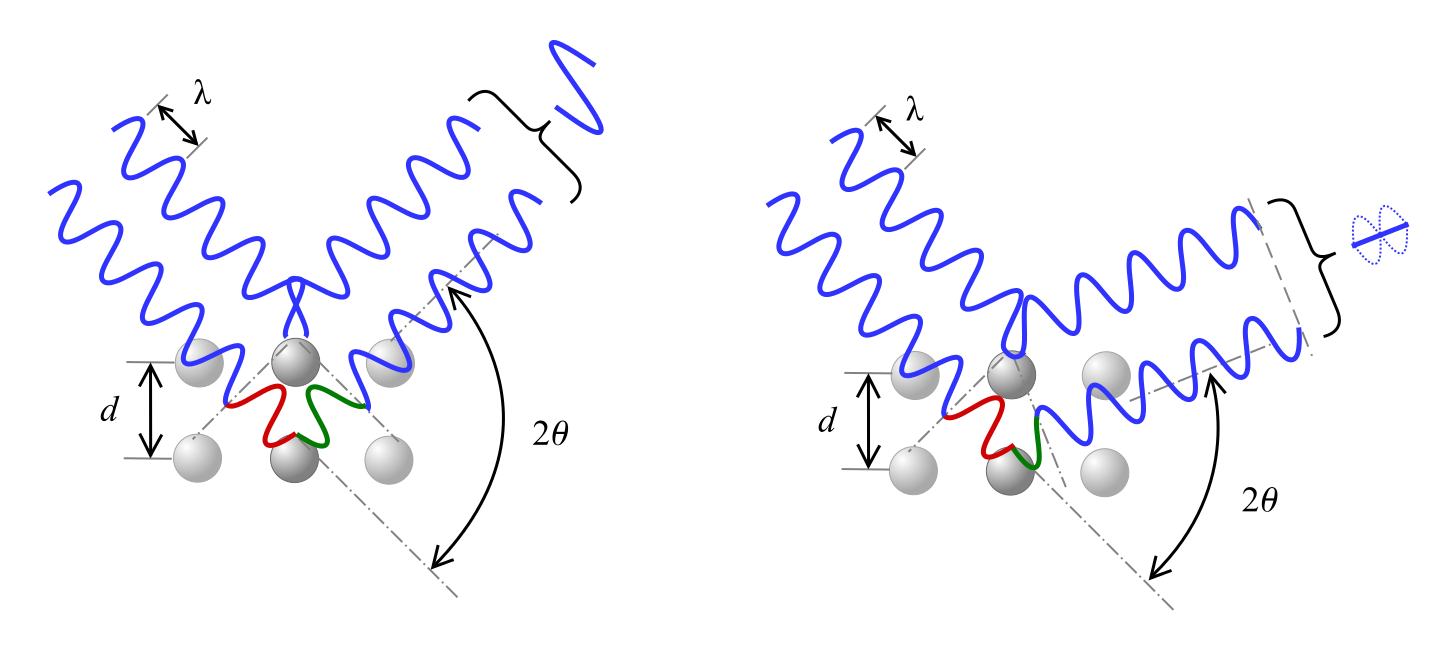
La ley de Bragg describe la relación para la interferencia constructiva, donde los rayos X de longitud de onda λ que inciden en el material con un ángulo θ son difractados por planos de cristal separados por la distancia d y n representa un número entero.
Como se muestra a continuación, un cambio de fase en la onda provoca una inferencia constructiva, como se muestra a la izquierda, o una interferencia destructiva, representada a la derecha, según el ángulo 2θ.
Ecuaciones para interpretar los resultados de la DRX
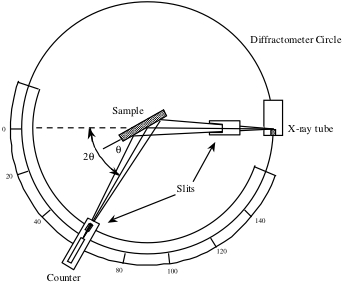
El contador, que se ve a continuación en un esquema de un difractómetro de rayos X, se gira sobre un rango de valores 2θ y registra la intensidad de la señal de rayos X reflejada por el cristal en cada posición. Esta intensidad medida en función de 2θ se utiliza para generar un perfil de picos.
Para los ángulos que satisfacen la condición de Bragg, se observará un pico en la señal de rayos X debido a la interferencia constructiva. Estos picos se utilizan para identificar las direcciones del cristal y calcular los parámetros de la red. Para los sistemas cúbicos, el espaciado interplanar, d, puede calcularse mediante la siguiente ecuación derivada de la geometría del cristal, donde a es el parámetro de red y h, k y l son los índices de Miller.
Combinando la ley de Bragg y el espaciado interplanar se obtiene la siguiente ecuación.
Aquí, hemos movido todas las constantes al lado izquierdo de la ecuación, lo que nos permite comparar las relaciones de los valores de sin2(θ) y los índices de Miller entre diferentes picos.
Cuando la onda electromagnética incidente incide en el material de la muestra, los electrones que residen en el material son perturbados en un patrón oscilante, lo que genera nuevos rayos X y dispersa eficazmente las ondas de luz incidentes. Se producen dos tipos de dispersión: la dispersión coherente o elástica, en la que los electrones oscilantes fuertemente unidos dispersan los rayos X de la misma longitud de onda, y la dispersión incoherente, que se produce cuando los electrones poco unidos se ponen en movimiento oscilatorio y generan rayos X de diferente energía. La difracción de rayos X mide la intensidad de los rayos X dispersados de forma coherente, que alcanza su punto máximo allí donde las ondas interfieren de forma constructiva. El factor de dispersión atómica puede definirse como una relación entre la amplitud de la onda dispersada por un átomo dividida por la amplitud de la onda dispersada por un solo electrón. Esta relación describe esencialmente la eficiencia de dispersión de un átomo para una dirección determinada.
Ejemplo de datos de DRX
Aquí están los datos recogidos de un experimento que hice durante mi curso de laboratorio de licenciatura tratando de identificar un metal desconocido basado en su estructura cristalina.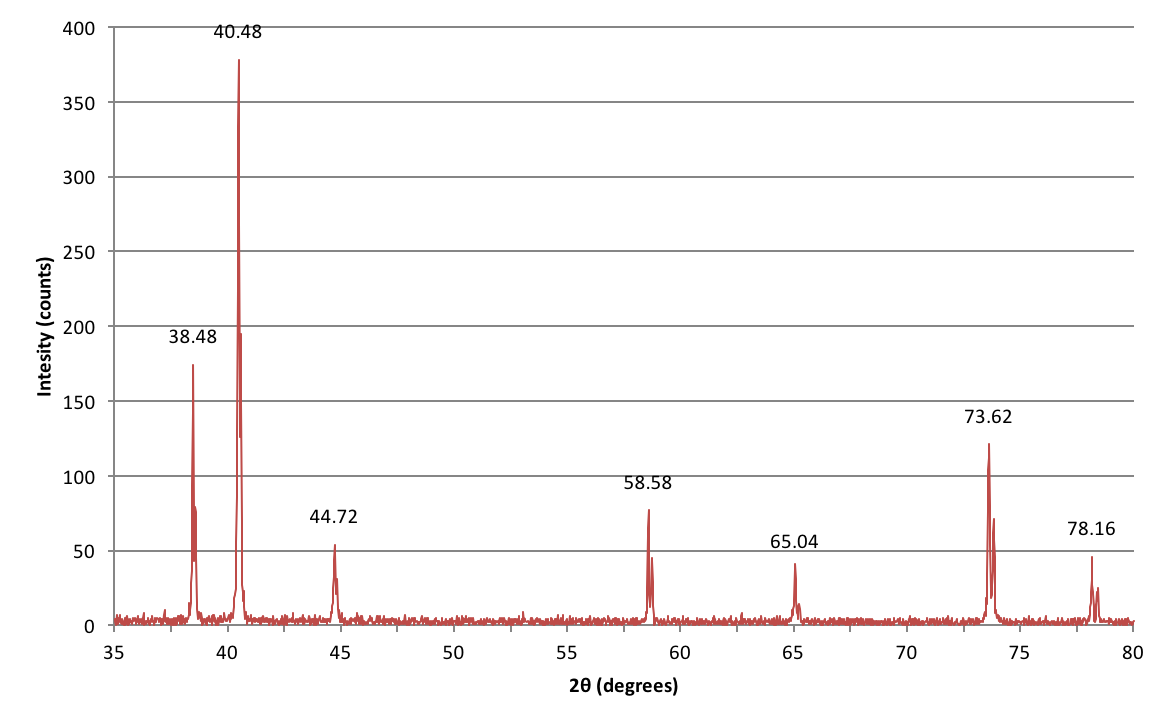
¿Cómo interpreto estos picos?
| Estructura cristalina | Condiciones |
|---|---|
| Simple cúbica | todos los valores h, k, l deben ser pares |
| Cúbico centrado en el cuerpo | h+k+l deben ser pares |
| Cúbico centrado en la cara | h, k, y l deben ser todos impares o todos pares |
Los factores de estructura tienen en cuenta los casos en los que un plano puede existir a medio camino entre dos planos vecinos y hace que se produzcan interferencias destructivas. Estos factores dan lugar a un conjunto de reglas para diferentes geometrías de estructuras cristalinas que determinan cuándo puede producirse una interferencia constructiva. La tabla anterior enumera los parámetros del índice de Miller en los que se producirá una interferencia constructiva. A continuación se muestra una tabla más extensa. Comparando las relaciones de sin2θ (denotadas como $Q^2$ en la segunda tabla) para diferentes picos de difracción, se puede determinar la estructura del cristal y los índices de Miller.
| Plano de cristal (hkl) | Q^2$ | Láminas espaciales desde las que son posibles las reflexiones | |||
|---|---|---|---|---|---|
| 100 | 1 | SC | |||
| 110 | 2 | SC | BCC | ||
| 111 | 3 | SC | FCC | DC | |
| 200 | 4 | SC | BCC | FCC | |
| 210 | 5 | SC | |||
| 211 | 6 | SC | BCC | ||
| – | 7 | ||||
| 220 | 8 | SC | BCC | FCC | DC |
| 300, 221 | 9 | SC | |||
| 310 | SC | BCC | |||
| 311 | 11 | SC | FCC | DC | |
| 222 | 12 | SC | BCC | FCC | |
| 320 | 13 | SC | |||
| 321 | 14 | SC | BCC | ||
| – | 15 | ||||
| 400 | 16 | SC | BCC | FCC | DC |
X-La difracción de rayos X tiene una amplia gama de aplicaciones para la caracterización de materiales. Puede utilizarse como método experimental para determinar experimentalmente el volumen de una celda unitaria para los cálculos teóricos de la densidad. Además, si el material está sometido a tensiones residuales, la red distorsionada mostrará una gama de espacios d que satisfacen la ley de Bragg, lo que da lugar a picos de difracción mucho más amplios. La anchura del pico de difracción también puede utilizarse para determinar el tamaño de las partículas.