Ordenación topológica de grafos acíclicos dirigidos

Introducción

En informática, un grafo acíclico dirigido (DAG) es un grafo dirigido sin ciclos. En este tutorial, mostraremos cómo hacer una ordenación topológica en un DAG en tiempo lineal.

Ordenación topológica

En muchas aplicaciones, utilizamos grafos acíclicos dirigidos para indicar las precedencias entre eventos. Por ejemplo, en un problema de programación, hay un conjunto de tareas y un conjunto de restricciones que especifican el orden de estas tareas. Podemos construir un DAG para representar las tareas. Las aristas dirigidas del DAG representan el orden de las tareas.

Consideremos un problema de cómo una persona puede vestirse para una ocasión formal. Hay que ponerse varias prendas, como calcetines, pantalones, zapatos, etc. Algunas prendas deben ponerse antes que las otras. Por ejemplo, hay que ponerse los calcetines antes que los zapatos. Algunas prendas pueden ponerse en cualquier orden, por ejemplo, los calcetines y los pantalones. Podemos utilizar un DAG para ilustrar este problema:

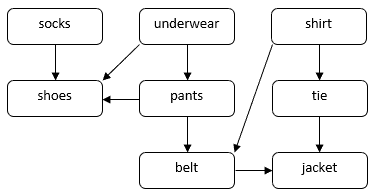
En este DAG, los vértices corresponden a las prendas de vestir. Una arista directa en el DAG indica que tenemos que ponernos la prenda antes que la prenda . Nuestra tarea consiste en encontrar un orden para poner todas las prendas respetando las restricciones de dependencia. Por ejemplo, podemos poner las prendas en el siguiente orden:

Una ordenación topológica de un DAG es una ordenación lineal de todos sus vértices tal que si contiene una arista , entonces aparece antes que en la ordenación. Para un DAG, podemos construir una ordenación topológica con un tiempo de ejecución lineal al número de vértices más el número de aristas, que es .

Algoritmo de Kahn

En un DAG, cualquier camino entre dos vértices tiene una longitud finita ya que el grafo no contiene un ciclo. Sea el camino más largo desde (vértice origen) hasta (vértice destino). Como es el camino más largo, no puede haber ninguna arista entrante a . Por lo tanto, un DAG contiene al menos un vértice que no tiene ninguna arista entrante.

3.1. Algoritmo de Kahn

En el algoritmo de Kahn, construimos una ordenación topológica en un DAG encontrando los vértices que no tienen aristas entrantes:

En este algoritmo, primero calculamos los valores de grado interno de todos los vértices.

Entonces, empezamos con un vértice cuyo grado interno es 0 y lo ponemos al final de la lista de salida. Una vez que elegimos un vértice, actualizamos los valores de grado interno de sus vértices adyacentes porque el vértice y sus aristas de salida se eliminan del grafo.

Podemos repetir el proceso anterior hasta elegir todos los vértices. La lista de salida es entonces una ordenación topológica del grafo.

3.2. Complejidad temporal

Para calcular los in-degrees de todos los vértices, necesitamos visitar todos los vértices y aristas de . Por lo tanto, el tiempo de ejecución es para los cálculos de in-degree. Para evitar calcular estos valores de nuevo, podemos utilizar una matriz para mantener un registro de los valores de grado interno de estos vértices. Dentro del bucle while, también necesitamos visitar todos los vértices y aristas. Por lo tanto, el tiempo total de ejecución es .

Búsqueda en profundidad

También podemos utilizar un algoritmo de Búsqueda en profundidad (DFS) para construir la ordenación topológica.

4.1. Antes de abordar el aspecto de la ordenación topológica con DFS, comencemos por revisar un algoritmo estándar y recursivo de DFS en el gráfico:

En el algoritmo estándar de DFS, comenzamos con un vértice aleatorio en y marcamos este vértice como visitado. Luego, llamamos recursivamente a la función dfsRecursive para visitar todos sus vértices adyacentes no visitados. De esta manera, podemos visitar todos los vértices de en tiempo.

Sin embargo, ya que estamos poniendo cada vértice en la lista inmediatamente cuando lo visitamos, y ya que podemos empezar en cualquier vértice, el algoritmo DFS estándar no puede garantizar la generación de una lista topológicamente ordenada.

Veamos lo que tenemos que hacer para abordar esta deficiencia.

4.2. Algoritmo de ordenación topológica basado en DFS

Podemos modificar el algoritmo DFS para generar una ordenación topológica de un DAG. Durante el recorrido DFS, después de que todos los vecinos de un vértice son visitados, entonces lo ponemos al frente de la lista de resultados . De este modo, nos aseguramos de que aparezca antes que todos sus vecinos en la lista ordenada:

Este algoritmo es similar al algoritmo DFS estándar. Aunque seguimos empezando con un vértice aleatorio, no ponemos el vértice en la lista inmediatamente una vez que lo visitamos. En su lugar, primero visitamos todos sus vecinos recursivamente y luego ponemos el vértice al frente de la lista. Por lo tanto, si contiene una arista , entonces aparece antes de en la lista.

El tiempo de ejecución global es también , ya que tiene la misma complejidad de tiempo que el algoritmo DFS.

Conclusión

En este artículo, hemos mostrado un ejemplo de ordenación topológica en un DAG. Además, discutimos dos algoritmos que pueden hacer un ordenamiento topológico en tiempo.

La implementación en Java del algoritmo de ordenamiento topológico basado en DFS está disponible en nuestro artículo sobre Depth First Search in Java.