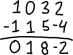Volver al índice de lecciones | Hacer las lecciones en orden | Página para imprimir
Operaciones de la fila de la matriz (página 1 de 2)
«Operaciones» es un término matemático para «procedimientos». Las cuatro «operaciones básicas» con números son la suma, la resta, la multiplicación y la división. Para las matrices, hay tres operaciones básicas con las filas; es decir, hay tres procedimientos que se pueden hacer con las filas de una matriz.
La primera operación es el cambio de fila. Por ejemplo, dada la matriz:

…puede cambiar las filas para poner la matriz en una disposición de filas más agradable, así:
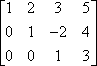
El cambio de filas se indica a menudo dibujando flechas, así:

Al cambiar las filas, tenga cuidado de copiar las entradas correctamente.
La segunda operación es la multiplicación de filas. Por ejemplo, dada la siguiente matriz:

…se puede multiplicar la primera fila por -1 para obtener un valor inicial positivo en la primera fila:
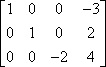
Esta multiplicación de filas se suele indicar utilizando una flecha con la multiplicación indicada encima, así:
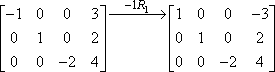
El «-1R1» indica la operación real. El «-1» dice que hemos multiplicado por uno negativo; el «R1» dice que estábamos trabajando con la primera fila. Obsérvese que las filas segunda y tercera se copiaron, sin cambios, en la segunda matriz. La multiplicación sólo se aplicó a la primera fila, por lo que las entradas de las otras dos filas se llevaron sin cambios.
Puedes multiplicar por lo que quieras. Por ejemplo, para obtener un 1 inicial en la tercera fila de la matriz anterior, puedes multiplicar la tercera fila por un medio negativo:

Como no has hecho nada con la primera y segunda filas, esas entradas se han copiado sin cambios en la nueva matriz.
Puedes hacer más de una multiplicación de filas en el mismo paso, por lo que podrías haber hecho los dos pasos anteriores en un solo paso, así:
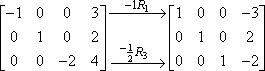
Es una buena idea utilizar algún tipo de notación (como las flechas y los subíndices de arriba) para que puedas hacer un seguimiento de tu trabajo. Las matrices son muy complicadas, sobre todo si las haces a mano, y las anotaciones pueden facilitar la comprobación de tu trabajo más adelante. También impresionará a su profesor.
La última operación de fila es la suma de filas. La suma de filas es similar al método de «adición» para resolver sistemas de ecuaciones lineales. Supón que tienes el siguiente sistema de ecuaciones:
x + 3y = 1
-x + y = 3 Copyright © Elizabeth Stapel 2003-2011 All Rights Reserved
Publicidad
Podrías empezar a resolver este sistema sumando las columnas para obtener 4y = 4:
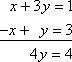
Puedes hacer algo parecido con las matrices.Por ejemplo, dada la siguiente matriz:

… puedes «reducir» (conseguir más ceros a la izquierda) la segunda fila añadiéndole la primera fila (el objetivo general con las matrices en esta fase es conseguir un «1» -o «0’s» y luego un «1»- al principio de cada fila de la matriz). Cuando redujiste el sistema lineal de dos ecuaciones mediante la adición, dibujaste una barra de «igual» en la parte inferior y sumaste hacia abajo. Cuando utilices la adición en una matriz, tendrás que coger papel de borrador, porque no querrás intentar hacer el trabajo dentro de la matriz. Así que añade las dos filas en tu papel de borrador:
|
Trabajo de borrador – |
|
Esta es tu nueva segunda fila; la escribirás en lugar de la antigua segunda fila. El resultado será así:
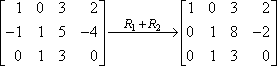
En este caso, el «R1 + R2» de la flecha significa «he añadido la fila uno a la fila dos, y éste es el resultado que he obtenido». Como la fila uno no cambió realmente, y como no hicimos nada con la fila tres, estas filas se copian en la nueva matriz sin cambios.
Top | 1 | 2 | Volver al índice siguiente >>
|
Cite este artículo como: |
Stapel, Elizabeth. «Operaciones de fila de la matriz». Purplemath. Disponible en 2016
|