Requisito previo – Fundamentos de la teoría de grafos – Conjunto 1
Un grafo es una estructura que consiste en un conjunto de objetos en el que algunos pares de los mismos están en cierto sentido «relacionados». Los objetos del grafo corresponden a vértices y las relaciones entre ellos a aristas. Un gráfico se representa en forma de diagrama como un conjunto de puntos que representan vértices conectados por líneas o curvas que representan aristas.
Formalmente,
«Un gráfico 
está formado por 
, un conjunto no vacío de vértices (o nodos) y 
, un conjunto de aristas. Cada arista tiene uno o dos vértices asociados a ella, llamados sus puntos finales.»
Tipos de grafos :Hay varios tipos de grafos que se distinguen en base a las aristas, su dirección, su peso, etc.
1. Gráfico simple: un gráfico en el que cada arista conecta dos vértices diferentes y en el que no hay dos aristas que conecten el mismo par de vértices se llama gráfico simple. Por ejemplo, considere el siguiente gráfico –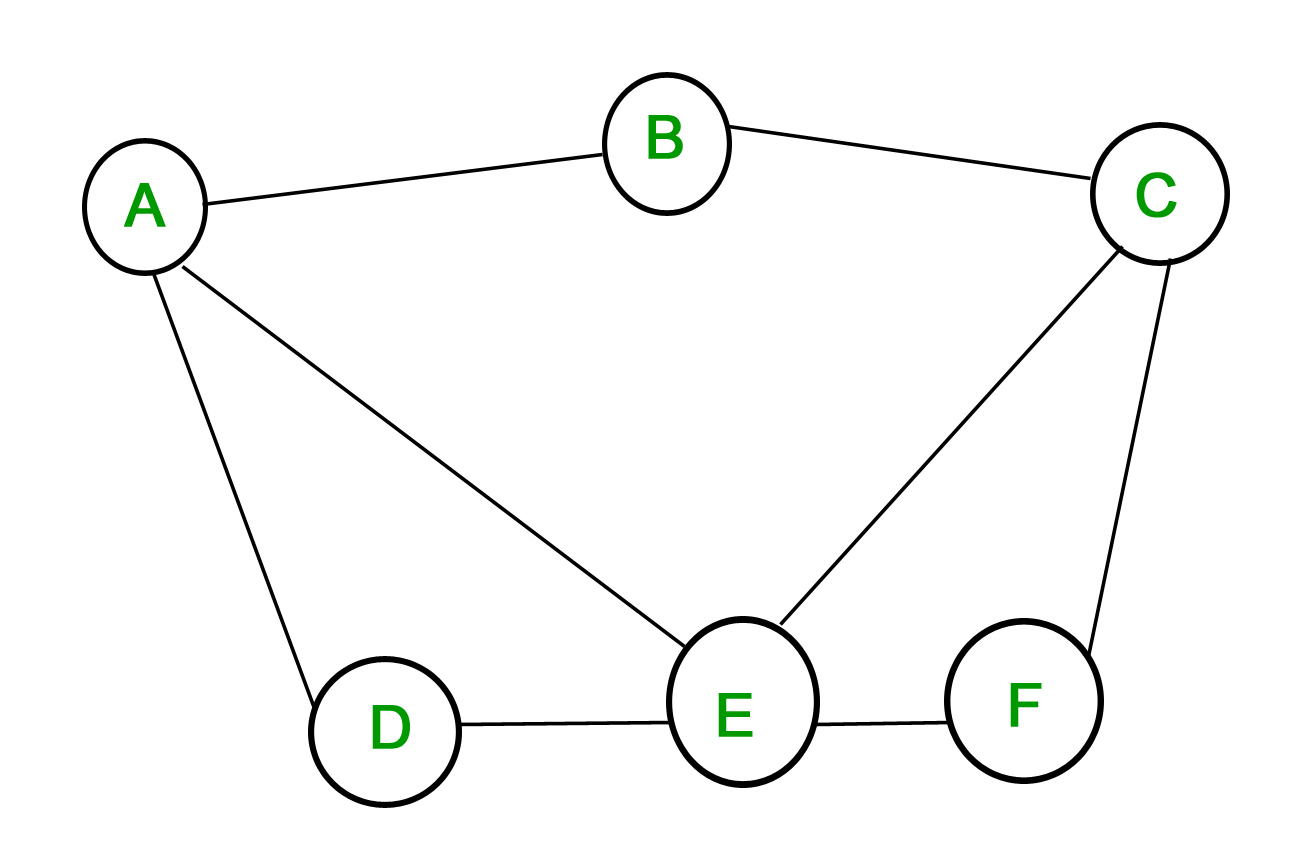
El gráfico anterior es un gráfico simple, ya que ningún vértice tiene un bucle propio y no hay dos vértices que tengan más de una arista que los conecte.
Las aristas se denotan por los vértices que conectan- 
es la arista que conecta los vértices 
y 
.
2. Multigráfico – Un gráfico en el que múltiples aristas pueden conectar el mismo par de vértices se llama multigráfico.
Como puede haber múltiples aristas entre el mismo par de vértices, la multiplicidad de la arista indica el número de aristas entre dos vértices.
El gráfico anterior es un multigráfico ya que hay múltiples aristas entre y 
. La multiplicidad de la arista 
es 2.
En algunos grafos, a diferencia del anterior, las aristas son dirigidas. Esto significa que la relación entre los objetos es unidireccional y no bidireccional. La dirección de las aristas puede ser importante en algunas aplicaciones.
En función de si las aristas son dirigidas o no podemos tener grafos dirigidos y grafos no dirigidos. Esta propiedad se puede extender a los grafos simples y a los multigrafos para obtener grafos simples dirigidos o no dirigidos y multigrafos dirigidos o no dirigidos.
Terminología básica de los grafos :
En la discusión anterior ya se han explicado algunos términos relativos a los grafos como vértices, aristas, aristas dirigidas y no dirigidas, etc. Hay más términos que describen las propiedades de los vértices y aristas.
- Adyacencia – En un grafo
se dice que dos vértices 
y 
son adyacentes si son los extremos de una arista. Se dice que la arista 
es incidente con los vértices.
En caso de que la arista sea dirigida, se dice que es adyacente a y que es adyacente de . Aquí, se dice que es el vértice inicial y se dice que es el vértice terminal. - Grado – El grado de un vértice es el número de aristas que inciden en él, excepto el bucle propio que contribuye dos veces al grado del vértice. El grado de un vértice se denota como
.
En el caso de los grafos dirigidos, el grado se clasifica además como grado de entrada y grado de salida. El grado de entrada de un vértice es el número de aristas con el vértice dado como vértice terminal. El grado de salida de un vértice es el número de aristas con el vértice dado como vértice inicial. El grado de entrada se denota como
y el grado de salida se denota como 
.
Por ejemplo, en el gráfico dirigido que se muestra arriba y que representa los vuelos entre ciudades, el grado de entrada del vértice «Delhi» es 3 y su grado de salida también es 3.
Nota: Si un vértice tiene grado cero, se llama aislado. Si el grado es uno entonces se llama colgante.
Teorema de la mano :
Qué se obtiene si se suman los grados de todos los vértices de un grafo. En el caso de un grafo no dirigido, cada arista contribuye dos veces, una por su vértice inicial y otra por su vértice terminal. Por tanto, la suma de grados es igual al doble del número de aristas. Este hecho se recoge en el teorema del apretón de manos.
Let be an undirected graph with edges. ThenIn case G is a directed graph,
El teorema del apretón de manos, para grafos no dirigidos, tiene un resultado interesante –
An undirected graph has an even number of vertices of odd degree.
Prueba : Sean 
y 
los conjuntos de vértices de grados pares e impares respectivamente.
Sabemos por el teorema del apretón de manos que,
Entonces,
La suma de grados de los vértices con grados pares es par. El LHS también es par, lo que significa que la suma de grados de los vértices con grados impares debe ser par.
Por tanto, el número de vértices con grado impar es par.
Algunos grafos simples especiales :
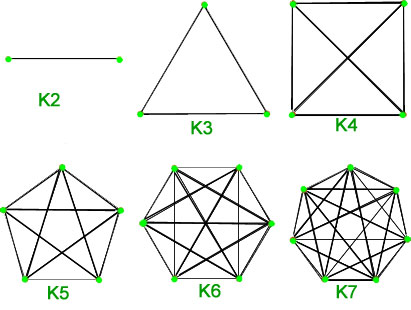
1. Grafos completos – Un grafo simple de 
vértices que tiene exactamente una arista entre cada par de vértices se llama grafo completo. Un grafo completo de vértices se denomina 
. El número total de aristas es n*(n-1)/2 con n vértices en el grafo completo.
2. Ciclos – Los ciclos son grafos simples con vértices 
y aristas 
. Un ciclo con vértices se denomina 
. El número total de aristas es n con n vértices en el gráfico del ciclo.
3. Ruedas – Una rueda es igual que un ciclo, con un vértice adicional que está conectado a todos los demás vértices. Las ruedas de vértices con 1 vértice adicional se denotan por 
. El número total de aristas es 2*(n-1) con n vértices en el gráfico de rueda.
4. Hipercubo – El Hipercubo o n-cubo es un gráfico con 
vértices representados cada uno por una cadena de n bits. Los vértices que difieren como máximo en 1 bit están conectados por aristas. Un hipercubo de vértices se denota por 
. El número total de aristas es n*
con vértices en el gráfico cúbico.
5. Grafos bipartitos – Se dice que un grafo simple es bipartito si su conjunto de vértices puede dividirse en dos conjuntos disjuntos tales que cada arista en tiene su vértice inicial en el primer conjunto y el vértice terminal en el segundo. El número total de aristas es (n*m) con (n+m) vértices en el grafo bipartito.
Teorema – Un grafo simple es bipartito si y sólo si es posible asignar uno de dos
colores diferentes a cada vértice del grafo de forma que no haya dos adyacentes con el
mismo color.
Un grafo bipartito con 
y vértices en sus dos subconjuntos disjuntos se dice que es completo si hay una arista desde cada vértice del primer conjunto a cada vértice del segundo conjunto, para un total de 
aristas. Un grafo bipartito completo con vértices en el primer conjunto y vértices en el segundo conjunto se denota como 
.
Preguntas del Rincón del CS del GATE
Practicar las siguientes preguntas te ayudará a comprobar tus conocimientos. Todas las preguntas han sido formuladas en GATE en años anteriores o en los Mock Tests de GATE. Es muy recomendable que las practiques.
1. GATE CS 2013, Pregunta 25
2. GATE CS 2014 Set-1, Pregunta 61
3. GATE CS 2006, Pregunta 71
4. GATE CS 2002, Pregunta 25
5. GATE CS 2004, Question 37
6. GATE CS 2014 Set-2, Question 13
Referencias-
Gráficos – Wikipedia
Matemáticas discretas y sus aplicaciones, por Kenneth H Rosen
Este artículo ha sido aportado por Chirag Manwani. Si te gusta GeeksforGeeks y quieres contribuir, también puedes escribir un artículo en contribute.geeksforgeeks.org o enviarlo por correo a [email protected]. Verás tu artículo en la página principal de GeeksforGeeks y ayudarás a otros Geeks.