¿Cuántos lados tiene un círculo?

Es una pregunta de los deberes de la escuela primaria que causa desacuerdo entre los matemáticos experimentados. Para encontrar la respuesta correcta, recurrí al más riguroso de los instrumentos científicos, la encuesta de Twitter:

En retrospectiva, me arrepiento de no haber incluido la opción «ninguna de las anteriores», pero más adelante hablaré de ello. En este post voy a repasar estas tres respuestas (y la de «ninguna de las anteriores»), y a discutir sus pros y sus contras según mi punto de vista, antes de revelar dramáticamente la respuesta correcta.

Pero primero: ¿por qué no podemos dar directamente la respuesta correcta? Las palabras de la pregunta no tienen ningún misterio. Todos sabemos qué es un «círculo», qué significa contar «cuántos» de algo y qué es un «lado»… ¿o no? He aquí las definiciones (aproximadas) que destilé de las conversaciones con dos alumnos de primaria que habían recibido esta pregunta:

1. Línea que forma parte del límite de una forma de una figura plana.

El propósito de decir figura plana en lugar de «forma» aquí es que queremos formas que viven en 2 dimensiones (por ejemplo, cuadrados o círculos, pero no esferas o cubos). La siguiente cuestión es qué es una «línea» en la definición 1. He aquí una variante que lo precisa:

2. Una línea recta que forma parte del límite de una figura plana.

Si escribes «define: lado» en Google, la definición más relevante es:

Una figura rectilínea es aquella que se construye con líneas rectas. Así que esta definición es un perfeccionamiento de la definición 2, y nos permite afirmar que un cuadrado tiene cuatro lados, pero a primera vista no tiene nada que decir sobre las figuras planas no rectilíneas, como los círculos.

¿Cuántos lados infinitos?

Creo que es una apuesta segura que los que respondieron a mi encuesta en Twitter tienen un nivel de educación matemática más alto que la media nacional. El hecho de que estuvieran divididos en esta pregunta, y que una pequeña mayoría seleccionara una respuesta que es bastante inasequible para el público habitual de esta pregunta (estudiantes de primaria), sugiere ciertamente que algo va mal en alguna parte.

Entonces, ¿tiene un círculo infinitos lados? Definitivamente es útil considerar un círculo como el límite de los polígonos de n lados a medida que n se hace más y más grande. Este es exactamente el enfoque que Arquímedes, Liu Hui e innumerables otros han utilizado a lo largo de los siglos para estudiar la geometría circular, incluyendo la obtención de aproximaciones para π.

Una edición de la dinastía Ming del siglo XVI del Jiuzhang suanshu (Nueve capítulos sobre el arte matemático), del siglo III de nuestra era.

A veces es absolutamente sensato, como taquigrafía conveniente, pensar que un círculo es como un polígono con infinitos lados.

Pero, como pedante insufrible que es un matemático, querría distinguir entre taquigrafía conveniente y verdad literal. Si nos empeñamos en que un círculo es realmente un polígono con infinitos lados, entonces se presenta la pregunta: ¿cuáles son los lados? Y seguramente la única respuesta plausible es: los puntos individuales del círculo. ¿Qué longitud tienen los llamados lados? Cero centímetros. ¿Y estos lados están separados por esquinas? Aparentemente no, o no hay esquinas en absoluto, o cada punto es a la vez un lado y una esquina.

Yo diría que los lados de longitud cero son… un concepto problemático. ¿Cómo puedes saber si tienes alguno? Por ejemplo, supongamos que estoy estudiando un sistema en el que un cuadrado surge como límite de octógonos como este:

En esta situación, bien podría tener sentido para mí pensar que mi cuadrado tiene ocho lados, cuatro de los cuales tienen longitud cero. Pero si insistiera en que mi cuadrado (perfectamente ordinario) tiene realmente ocho lados, podríais levantar una ceja.

Así que ésta -la respuesta ganadora de mi encuesta- es la única que voy a declarar definitivamente errónea, a la vez que es la única que ofrece alguna idea geométrica. ¿Una paradoja? En realidad, no. Razonar por analogía es una valiosa habilidad en las matemáticas y en la vida; al mismo tiempo es importante aferrarse a la comprensión de que eso es lo que estamos haciendo.

Por infinitos lados: geométricamente esclarecedor.
Contra infinitos lados: cuadrados de ocho lados.

Saliendo por la tangente 1: apeirogones

Aunque un círculo no lo sea, ¿existen los polígonos con infinitos lados? Bueno, hay una palabra para describir tal cosa: un apeirógono. Un apeirón regular tendría entonces lados de igual longitud (no nula) con ángulos iguales entre ellos. La única opción aquí es este objeto estupendamente poco excitante:

Si te opones a que esto sea un «polígono» (ya sea por los ángulos de 180° o por la cadena de aristas que no se cierran en un bucle), ¿qué tal algo así? empezar en la parte inferior de un círculo, y en cada etapa moverse alrededor de la mitad de lo que queda del círculo, y sustituir el arco que acabas de recorrer por una arista recta:

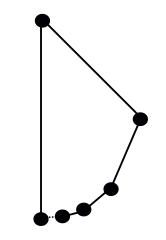
¿Es esto un auténtico polígono? Una vez más, depende de tus términos. Según una de las definiciones más comunes, la de «cadena poligonal cerrada», esto no cumple los requisitos, ya que la esquina inicial (abajo a la izquierda) sólo se conecta a una arista. Pero está muy cerca de serlo: ese punto es el límite de una secuencia de aristas desde la derecha, lo que convierte a esta forma en una «curva cerrada no autointersectiva a trozos», otra definición de polígono que la gente utiliza.

Si dejamos nuestro mundo euclidiano habitual y entramos en el espacio hiperbólico, entonces no hay ambigüedad. Los apeirógonos (incluso los regulares) simplemente existen:

Un mosaico del plano hiperbólico por apeirógonos regulares. (Por Anton Sherwood – Obra propia, Dominio Público, https://commons.wikimedia.org/w/index.php?curid=13260274 )

Saliendo por la tangente 2: puntos extremos

Podría ser más defendible decir que un círculo tiene infinitas esquinas que infinitos lados (aunque no es una pregunta que parezca plantearse muy a menudo). Para empezar, si una esquina de un cuadrado es un punto en el que su línea límite no es recta, entonces cada punto del círculo cumple eso. De forma más sofisticada, existe la noción de punto extremo de una forma: es cualquier punto por el que se puede trazar un segmento de recta que toque la forma sólo en ese punto exacto. En el caso de un cuadrado y de muchas formas conocidas, los puntos extremos coinciden exactamente con las esquinas. Cada punto en el límite del círculo es un punto extremo, por lo que es cierto que un círculo tiene infinitos.

Podríamos preocuparnos de que algunas formas como este chevron tengan esquinas que no son puntos extremos:

Aquí la esquina central inferior no es un punto extremo (las otras tres esquinas sí lo son). Lo que falla es que esta forma no es convexa (a grandes rasgos, tiene algunos trozos que sobresalen demasiado). Un círculo es convexo, así que quizá no haya que preocuparse. Otra posibilidad es definir una «esquina» como un punto extremo de la forma en cuestión o de su complemento, es decir, el plano completo con la forma recortada. Este enfoque permitiría detectar las esquinas de todos los polígonos, incluido el chevron. En el caso de las curvas suaves, identificaría todos los puntos límite como «esquinas», excepto los puntos de inflexión (lo cual no es descabellado, ya que podríamos argumentar que el límite es recto allí).

¿Un lado?

En la escuela primaria, parece que «uno» es la respuesta que se lleva la palma. Y hay una justificación medianamente decente. Recuerda la definición 1 anterior:

1. Línea que forma parte del límite de una figura plana.

La cuestión inmediata es qué cuenta como «línea», especialmente si no insistimos en la rectitud. Si nos relajamos demasiado en esto, entonces podría decirse que cualquier figura plana tiene «un lado», en el mismo sentido que tiene un límite, un perímetro o una circunferencia. Pero esto tiene que estar mal, ya que seguramente queremos que un cuadrado tenga cuatro. Pues bien, un cuadrado tiene cuatro puntos en los que no es liso, con cuatro secciones lisas en medio. Tal vez sean las secciones lisas las que estamos contando todo el tiempo. Así que implícitamente tenemos un nuevo refinamiento de la definición 1 (y también aprovechamos la oportunidad para deshacernos del vago término «figura»):

4. Cada sección suave de una curva cerrada a trozos.

Una «curva cerrada» es aquella que hace un bucle para encontrarse consigo misma, de modo que no tiene extremos libres. «Suave a trozos» significa que está construida a partir de secciones suaves, que se encuentran en puntos aislados no suaves. Es perfectamente legítimo querer contar las secciones lisas de la frontera de una forma así, y no es en absoluto escandaloso utilizar la palabra «lado» al hacerlo. Así que ciertamente no estoy diciendo que esta sea definitivamente la respuesta incorrecta.

La cuestión es si esa interpretación de «lado» no es meramente coherente, sino lo suficientemente natural como para que pueda ser simplemente presumida sin ser declarada explícitamente (que rara vez o nunca lo es). ¿Qué ocurre cuando la suavidad y la rectitud coinciden de forma diferente? Consideremos esta forma de lápida, creada sustituyendo la parte superior de un cuadrado por un semicírculo de igual diámetro.

Tiene dos secciones lisas (la línea inferior y el resto) pero tres bordes rectos (más una pieza curva que une suavemente dos de ellos). Entonces, ¿cuántos lados tiene? He vuelto a consultar a mis amigos de Twitter:

Esta vez debería haber incluido «infinitamente numerosos» como opción, aunque eso se puede absorber en «Ninguna de las anteriores». Cualquiera que vote que el círculo tiene infinitos lados debería votar automáticamente «Ninguna de las anteriores» aquí, a menos que -una advertencia importante- la naturaleza de esta forma indique al lector una noción diferente de «lado». El hecho de que las opciones más populares en estas dos encuestas sean incompatibles sugiere que este puede ser el caso (o al menos refuerza que las aguas están turbias).

Aunque dos es una respuesta perfectamente respetable, compatible con la definición 4 anterior y con la unilateralidad de un círculo, no estoy satisfecho de que sea definitivamente la correcta, o de que tres o cuatro sean categóricamente incorrectas. Depende de lo que se quiera contar: secciones lisas, bordes rectos, o bordes rectos más lo que sobre, cualquiera de los cuales podría ser la respuesta deseada dependiendo del contexto (más sobre esto más adelante). En relación con esto, no estoy seguro de que contar el número de secciones lisas coincida plenamente con mi intuición de la palabra «lado». Después de todo, las dos secciones lisas de la lápida están -creo que es justo decirlo- «en lados opuestos». ¿Estamos realmente satisfechos de que formen parte simultáneamente del «mismo lado»?

Podrías protestar que estoy confundiendo dos significados diferentes de «lado», que la terminología a veces choca, y que simplemente tenemos que vivir con ello. Sin embargo, no estoy tan seguro. El objetivo de este ejercicio es extrapolar una situación (figuras rectilíneas) en la que las dos nociones encajan bastante bien. Si hubiera una nueva idea que recogiera todo lo que nos gusta del original, pero que también se aplicara a una categoría más amplia de formas, entonces sería la única respuesta correcta. Pero si todos nuestros intentos de generalización implican el sacrificio de aspectos deseables del original, quizá no haya una única generalización correcta. Hay diferentes opciones, con diferentes compensaciones, que podrían ser adecuadas en diferentes contextos (y si nos encontramos en una situación en la que hay más de una en juego, entonces se les podría dar diferentes nombres).

Aquí hay otra variación: una lápida de Weierstrass creada mediante la sustitución del borde superior de un cuadrado por una sección de la función de Weiestress, una línea infinitamente ondulada que no es suave en ninguna parte.

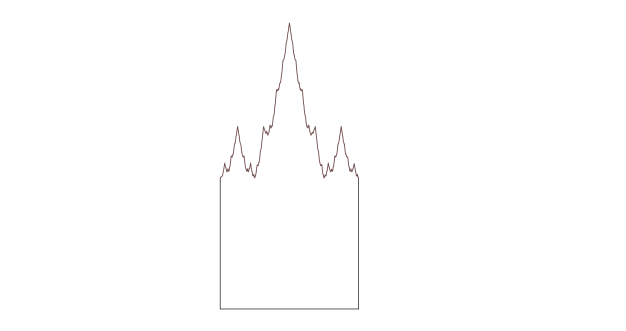
Aquí (y fíjate en la errata) está lo que mis amigos de Twitter hicieron de esto -aunque fueron menos los que se aventuraron a opinar:

A pesar del escepticismo de mis seguidores de Twitter, explicaré en un minuto por qué no creo que sea una tontería ver que esto tiene cuatro lados (uno de los cuales no es liso). Por otro lado, si prefieres que tus lados sean lisos, entonces tienes de nuevo la opción de ver que tiene infinitos lados (tres de los cuales tienen longitud 1, y el resto longitud 0), o que tiene 3 lados más un tramo de frontera definitivamente no liso.

Por un lado: una sola curva suave.
Contra un lado: el mismo lado en lados opuestos.

Saliendo por la tangente 3: lados contra aristas

¿Cuántos lados tiene un cuadrado? Cuatro. Cuántas aristas tiene? Cuatro. Entonces, ¿son las aristas y los lados lo mismo? No necesariamente. Aquí hay dos configuraciones que son -al menos discutiblemente- cada una de cuatro lados pero tienen 5 y 3 aristas respectivamente:

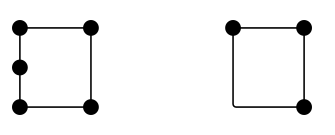
En general, yo diría que una «arista» es un objeto topológico, en el sentido de que su función, no su forma, es lo que importa. Piensa en el mapa del metro de Londres. Si se pregunta cuántas aristas hay en esa red, no tiene sentido sumar tramos rectos o lisos. Lo que cuenta son las conexiones entre estaciones (o vértices).

Como ya se ha mencionado, es común pensar en un polígono como una especie de red muy simple llamada cadena poligonal cerrada: una cadena de vértices (en este caso las esquinas del polígono), unidos con aristas, de tal manera que cada vértice se encuentra exactamente en dos aristas, y el conjunto forma un único bucle. En esta situación, las aristas y los lados coinciden, al igual que los vértices y las esquinas. Pero en general se puede romper esta concurrencia, como en las dos pequeñas redes de arriba.

Si quieres pensar en las cosas de forma teórica, pero los vértices no están claramente marcados, entonces tienes que adivinar dónde están. Con un polígono esto es fácil – los vértices están en las esquinas – que es la razón por la que el cambio entre los enfoques geométricos y topológicos es tan natural. Pero con otras formas, como cualquiera de las lápidas anteriores, puede no ser tan obvio. Sin embargo, en cada caso, si te dijeran que hay vértices en alguna parte, y te pidieran que los localizaras, creo que sería sensato adivinar que hay cuatro, a saber, las esquinas del cuadrado original, y que el borde superior se ha representado por alguna razón como una línea no recta. Y si queremos pensar en las cosas de esa manera, con cada una de las lápidas teniendo 4 bordes, entonces podría parecer extraño (¡aunque lógicamente coherente!) para insistir en que tienen algún otro número de lados (especialmente porque el lado superior está -a pesar de su propia geometría- claramente «en un lado» de la figura). De hecho, en lugar de adivinar, uno de mis corresponsales en Twitter me preguntó «¿Se han eliminado los dos vértices superiores?», una pregunta que sólo tiene sentido desde la perspectiva de la teoría de redes.

¿Dónde deja esto al círculo? El problema es que ningún punto del círculo tiene más derecho a ser vértice que otro. Así que, aunque es tentador (y de nuevo coherente) ver un círculo como una red con una arista, si vamos a insertar vértices, no hay ninguna razón obvia para preferir uno a cualquier otro número.

¿Podríamos verlo como una red sin vértices en absoluto, una especie de línea de metro sin estaciones? La concepción matemática habitual de una red no lo permitiría, pero eso no debería disuadirnos demasiado. Esto sugiere un enfoque puramente topológico. El problema es que, desde ese punto de vista, si bien un círculo puede ser una especie de red sin vértices y con una arista, también lo es un cuadrado (si es que la línea del metro está dispuesta así). En topología, un cuadrado es un círculo. (Esto no es una paradoja, es simplemente decir que el límite es un solo bucle, cuya forma no importa). Así que mientras este tipo de red tiene «una arista», obviamente un cuadrado no tiene «un lado», por lo que la relación entre lados (geométrica) y aristas (topológica) se ha vuelto a romper, al igual que en las dos pequeñas redes de la imagen anterior. Así que este enfoque no nos lleva muy lejos.

¿Sin lados?

Puede parecer paradójico argumentar que un círculo (o cualquier forma) no tiene «lados». Pero el argumento de la defensa es sencillo. Volvemos a la definición 2:

2. Línea recta que forma parte del límite de una figura plana.

Esta es una frase sencilla y fácilmente comprensible que recoge perfectamente los lados de un cuadrado. No hemos conseguido encontrar una generalización satisfactoria de la misma a las figuras curvas, así que lo mejor es quedarse con el original. Y un círculo no tiene ninguno.

Por no tener lados: cierto, según una noción sensata de «lado».
Contra no tener lados: suena a koan zen.

¿Nada de lo anterior?

Recuerda la definición proporcionada por Google:

3. Cada una de las líneas que forman el límite de una figura plana rectilínea.

Intentar aplicar esto a un círculo -una figura no rectilínea- no produce nada. La pregunta carece de tanto sentido como «¿Cuántos lados tiene el lunes?»

Dado que la definición 3 es la más oficial (la única de este post que no me he inventado yo o mis hijos), ¿no hace eso que «Ninguna de las anteriores» sea categóricamente la respuesta correcta? Tal vez. Por otro lado: cuando alguien nos plantea una pregunta, el principio de caridad quizá nos exija asumir que tiene sentido a menos que podamos establecer firmemente lo contrario, y las definiciones 1, 2, 4 y otras variantes lo hacen posible. Además, la definición 3 es lingüística y no formalmente matemática, y por lo tanto es descriptiva y no prescriptiva, por lo que no debemos atarnos a ella.

Por nada de lo anterior: mal funcionamiento semántico.
Contra nada de lo anterior: caridad dialógica.

La respuesta correcta

¿Qué me impulsó a escribir este post? Como innumerables alumnos de primaria, a mis hijos gemelos de cinco años -los alumnos de primaria mencionados al principio- les hicieron recientemente esta pregunta en sus deberes. Uno se decantó por el «1» y el otro por el «0», y he tratado de recoger y ampliar sus razonamientos más arriba. Creo que ambas respuestas son totalmente defendibles – y ninguna es definitivamente correcta.

Entonces, ¿qué deberías hacer si te hacen la pregunta: ¿Cuántos lados tiene un círculo? En mi opinión, la respuesta óptima es dirigirse al matemático de tu vida para que escriba un tratado de 3000 palabras sobre el tema, que luego podrás imprimir y entregar triunfalmente a tu desafortunado profesor. Pero en su defecto, lo mejor es seguir el ejemplo de Sócrates y responder a la pregunta con una contrapregunta: ¿Qué quieres decir con «lado»?

A fin de cuentas, contar hasta el cero, o hasta el uno, o negarse a responder a la pregunta, no nos dice prácticamente nada sobre la geometría de los círculos. Pero se puede ganar mucho desmenuzando las nociones familiares, eliminando o añadiendo condiciones adicionales, desafiando nuestra intuición al pasar de un contexto a otro ligeramente diferente, y tratando de escribir con precisión lo que queremos decir con un término particular en un entorno particular. En eso consisten las verdaderas matemáticas.

Notas al pie

Se podría hacer otra cosa: por ejemplo, elegir un punto de partida P en el círculo, desde el que medir la distancia alrededor de la circunferencia. Luego declarar que los puntos a una distancia racional de P son esquinas y el resto son lados. Esto tiene el efecto de producir un número contablemente infinito de ángulos y un número incontablemente infinito de lados. O se podría estipular lo contrario. Esto podría ser un ajuste conveniente para el enfoque del límite poligonal de los círculos, pero me costaría estar de acuerdo en que es lo suficientemente fácil u obvio como para ser considerado «la respuesta correcta».

Uno de mis corresponsales en Twitter estaba preocupado por lo suave que es la curva. Esta lápida es continuamente diferenciable pero no dos veces. Ciertamente sería interesante que mucha gente pensara que esto es una cuestión crítica, y probablemente se podría probar con una lápida infinitamente suave construida a partir de algo como esto, aunque no he pensado en los detalles.

Podríamos intentar formalizar esto de la siguiente manera: en un cuadrado (o cualquier polígono), un lado tiene la propiedad de que partiendo de cualquier posición en el interior, se puede cortar la forma en línea recta a través de su ubicación, de modo que el lado elegido está firmemente en un lado del corte. Esto no funciona para la lápida de dos lados: cualquier corte siempre cortará el lado largo. Podríamos debilitar esto diciendo que para que cuente como un lado, tiene que haber al menos una forma de cortar a través de la forma para que el lado esté en un lado del corte. Eso nos permitiría decir que la lápida tiene cuatro lados (aunque la sección curva no esté en un lado de los puntos de la región superior). Para el círculo sin embargo, su supuesto lado nunca está en un lado (por lo que se descartaría), y sólo la sección recta de un semicírculo contaría como un lado.

No es fácil llegar a una justificación rigurosa que funcione para ambas lápidas, pero estoy pensando más informalmente en términos de Puntos de Schelling: es decir, lugares que destacan por ser especiales por razones que pueden no ser fáciles de predecir de antemano.

Agradecimientos

Gracias a todos los que participaron o retuitearon mis encuestas, o discutieron esto conmigo en Twitter.