- La conectividad es un concepto básico de la teoría de grafos. Define si un gráfico está conectado o desconectado. Sin conectividad, no es posible recorrer un grafo desde un vértice a otro vértice.
- Se dice que un grafo es conectado si existe un camino entre cada par de vértices. De cada vértice a cualquier otro vértice debe haber algún camino que recorrer. Esto se llama la conectividad de un gráfico.
- Se dice que un gráfico está desconectado, si existen múltiples vértices y aristas desconectadas.
- Las teorías de conectividad de los gráficos son esenciales en las aplicaciones de red, el enrutamiento de las redes de transporte, la tolerancia de la red, etc.
Ejemplo
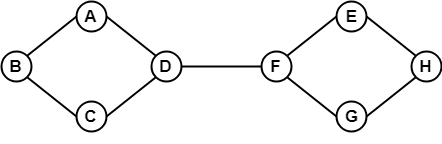
En el ejemplo anterior, es posible viajar de un vértice a otro vértice. En este caso, podemos viajar desde el vértice B hasta el H utilizando el camino B -> A -> D -> F -> E -> H. Por lo tanto, se trata de un grafo conexo.
Ejemplo
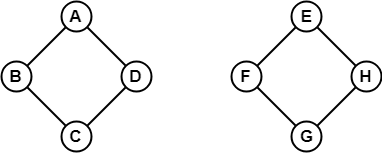
En el ejemplo anterior, no es posible viajar desde el vértice B hasta el H porque no hay ningún camino entre ellos directa o indirectamente. Por lo tanto, es un grafo desconectado.
Veamos algunos conceptos básicos de Conectividad.
Vértice de corte
Un solo vértice cuya eliminación desconecta un grafo se llama vértice de corte.
Sea G un grafo conectado. Un vértice v de G se llama vértice cortado de G, si G-v (Quitar v de G) resulta un grafo desconectado.
Cuando eliminamos un vértice de un grafo entonces el grafo se romperá en dos o más grafos. Este vértice se llama vértice de corte.
Nota: Sea G un grafo con n vértices:
- Un grafo conexo G puede tener un máximo de (n-2) vértices de corte.
- Quitar un vértice de corte puede dejar un grafo desconectado.
- Quitar un vértice puede aumentar el número de componentes de un grafo en al menos uno.
- Cada vértice no colgante de un árbol es un vértice cortado.
Ejemplo 1

Ejemplo 2
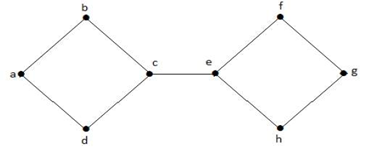
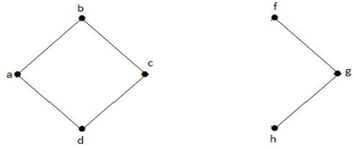
En el grafo anterior, el vértice ‘e’ es un vértice cortado. Después de eliminar el vértice ‘e’ del gráfico anterior el gráfico se convertirá en un gráfico desconectado.
Borde de corte (puente)
Una arista de corte o puente es una arista única cuya eliminación desconecta un gráfico.
Sea G un gráfico conectado. Una arista e de G se llama arista cortada de G, si G-e (Quitar e de G) resulta un grafo desconectado.
Cuando eliminamos una arista de un grafo entonces el grafo se romperá en dos o más grafos. Esta arista eliminada se llama arista de corte o puente.
Nota: Sea G un grafo con n vértices:
- Un grafo conexo G puede tener a lo sumo (n-1) aristas de corte.
- La eliminación de una arista de corte puede dejar un grafo desconectado.
- La eliminación de una arista puede aumentar el número de componentes de un grafo como máximo en uno.
- Una arista de corte ‘e’ no debe formar parte de ningún ciclo en G.
- Si existe una arista de corte, entonces también debe existir un vértice de corte porque al menos un vértice de una arista de corte es un vértice de corte.
- Si existe un vértice de corte, entonces no es necesaria la existencia de ninguna arista de corte.
Ejemplo 1
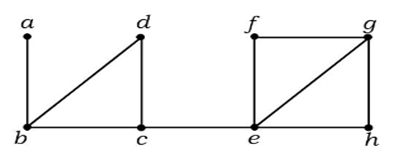
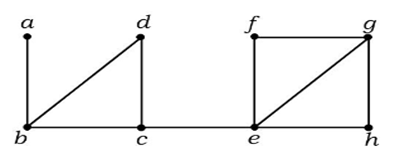
En el gráfico anterior, la arista (c, e) es una arista de corte. Después de eliminar esta arista del gráfico anterior, el gráfico se convertirá en un gráfico desconectado.
Ejemplo 2
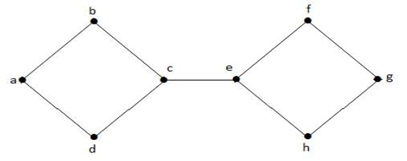
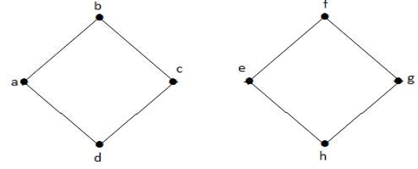
En el gráfico anterior, la arista (c, e) es una arista cortada. Después de eliminar esta arista del grafo anterior el grafo se convertirá en un grafo desconectado.
Conjunto de corte
En un grafo conexo G, un conjunto de corte es un conjunto S de aristas con las siguientes propiedades:
- La eliminación de todas las aristas en S desconecta G.
- La eliminación de algunas de las aristas (pero no todas) en S no desconecta G.
Ejemplo 1
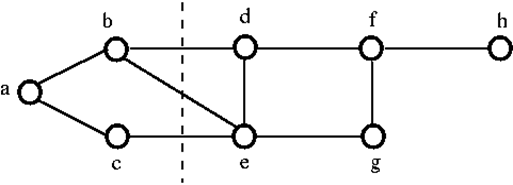
Para desconectar el gráfico anterior G, tenemos que eliminar las tres aristas. es decir, bd, be y ce. No podemos desconectarlo eliminando sólo dos de las tres aristas. Por lo tanto, {bd, be, ce} es un conjunto de corte.
Después de eliminar el conjunto de corte del gráfico anterior, se vería como sigue:
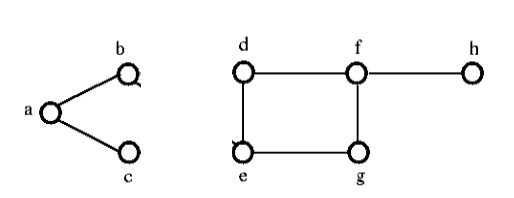
Conectividad de aristas
La conectividad de aristas de un gráfico conectado G es el número mínimo de aristas cuya eliminación hace que G esté desconectado. Se denota por λ(G).
Cuando λ(G) ≥ k, entonces se dice que el grafo G está conectado por k aristas.
Ejemplo
Veamos un ejemplo,
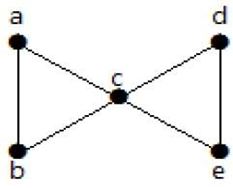
Del grafo anterior, al eliminar dos aristas mínimas, el grafo conectado se convierte en grafo desconectado. Por lo tanto, su conectividad de aristas es 2. Por lo tanto, el gráfico anterior es un gráfico conectado de 2 aristas.
Aquí están las siguientes cuatro formas de desconectar el gráfico mediante la eliminación de dos aristas:
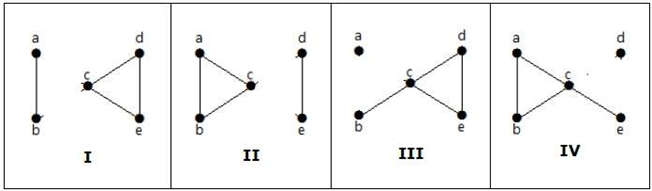
Conectividad de vértices
La conectividad (o conectividad de vértices) de un gráfico conectado G es el número mínimo de vértices cuya eliminación hace que G se desconecte o se reduzca a un gráfico trivial. Se denota por K(G).
Se dice que el grafo es k-conectado o k-vértices conectados cuando K(G) ≥ k. Para eliminar un vértice debemos eliminar también las aristas incidentes en él.
Ejemplo
Veamos un ejemplo:
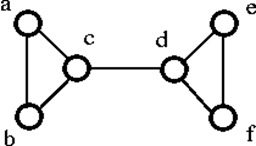
El grafo G anterior puede desconectarse eliminando el único vértice ya sea ‘c’ o ‘d’. Por lo tanto, su conectividad de vértices es 1. Por lo tanto, es un gráfico 1-conectado.