Cinética Química
Cinética Química
Es posible que esté familiarizado con las valoraciones ácido-base que utilizan fenolftaleína como indicador del punto final. Sin embargo, puede que no se haya dado cuenta de lo que ocurre cuando una solución que contiene fenolftaleína en presencia de un exceso de base se deja reposar durante unos minutos. Aunque la solución tiene inicialmente un color rosa, gradualmente se vuelve incolora a medida que la fenolftaleína reacciona con el ion OH- en una solución fuertemente básica.
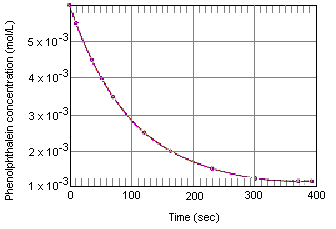
La siguiente tabla muestra lo que ocurre con la concentración de fenolftaleína en una solución que inicialmente tenía 0,005 M de fenolftaleína y 0,61 M de ion OH-. Como se puede ver al trazar estos datos en el gráfico siguiente, la concentración de fenolftaleína disminuye en un factor de 10 en un período de unos cuatro minutos.
Datos experimentales de la reacción entre la fenolftaleína y el exceso de base
Los experimentos como el que nos ha proporcionado los datos de la tabla anterior se clasifican como mediciones de cinética química (de una raíz griega que significa «moverse»). Uno de los objetivos de estos experimentos es describir la velocidad de reacción, es decir, la velocidad a la que los reactivos se transforman en productos de la reacción.
El término velocidad se utiliza a menudo para describir el cambio en una cantidad que se produce por unidad de tiempo. La tasa de inflación, por ejemplo, es el cambio en el coste medio de una colección de artículos estándar por año. La velocidad a la que un objeto se desplaza por el espacio es la distancia recorrida por unidad de tiempo, como las millas por hora o los kilómetros por segundo. En la cinética química, la distancia recorrida es el cambio en la concentración de uno de los componentes de la reacción. La velocidad de una reacción es, por tanto, el cambio en la concentración de uno de los reactivos![]() (X)
(X)![]() que se produce durante un periodo de tiempo
que se produce durante un periodo de tiempo![]() t.
t.
![]()
Problema de práctica 1:
Utilice los datos de la tabla anterior para calcular la velocidad a la que la fenolftaleína reacciona con el ion OH- durante cada uno de los siguientes períodos:
(a) Durante el primer intervalo de tiempo, cuando la concentración de fenolftaleína cae de 0,0050 M a 0,0045 M.
(b) Durante el segundo intervalo, cuando la concentración cae de 0,0045 M a 0,0040 M.
(c) Durante el tercer intervalo, cuando la concentración cae de 0,0040 M a 0,0035 M.
Haga clic aquí para comprobar su respuesta al problema de práctica 1.
Haga clic aquí para ver la solución del Problema de Práctica 1.
![]()
Tasa de Reacción Instantánea y la Ley de la Tasa para una Reacción
La tasa de la reacción entre la fenolftaleína y el ion OH no es constante; cambia con el tiempo. Como la mayoría de las reacciones, la velocidad de esta reacción disminuye gradualmente a medida que se consumen los reactivos. Esto significa que la velocidad de reacción cambia mientras se mide.
Para minimizar el error que esto introduce en nuestras mediciones, parece aconsejable medir la velocidad de reacción durante periodos de tiempo cortos comparados con el tiempo que tarda la reacción en producirse. Podríamos intentar, por ejemplo, medir el cambio infinitesimal en la concentración![]() d(X)
d(X)![]() que se produce en un periodo de tiempo infinitesimal. La relación de estas cantidades se conoce como velocidad instantánea de reacción.
que se produce en un periodo de tiempo infinitesimal. La relación de estas cantidades se conoce como velocidad instantánea de reacción.
![]()
La velocidad instantánea de reacción en cualquier momento puede calcularse a partir de una gráfica de la concentración del reactivo (o producto) frente al tiempo. El siguiente gráfico muestra cómo puede calcularse la velocidad de reacción para la descomposición de la fenolftaleína a partir de un gráfico de concentración en función del tiempo. La velocidad de reacción en cualquier momento en el tiempo es igual a la pendiente de una tangente dibujada a esta curva en ese momento.
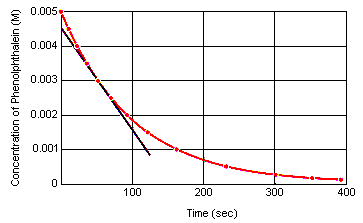
La velocidad instantánea de reacción puede medirse en cualquier momento entre el momento en que se mezclan los reactivos y la reacción alcanza el equilibrio.
![]()
Las leyes de velocidad y las constantes de velocidad
Se obtiene un resultado interesante cuando se calcula la velocidad instantánea de reacción en varios puntos a lo largo de la curva de la gráfica de la sección anterior. La velocidad de reacción en cada punto de esta curva es directamente proporcional a la concentración de fenolftaleína en ese momento.
Rata = k(fenolftaleína)
Debido a que esta ecuación es una ley experimental que describe la velocidad de la reacción, se denomina ley de velocidad de la reacción. La constante de proporcionalidad, k, se conoce como la constante de velocidad.
Problema de práctica 2:
Calcule la constante de velocidad para la reacción entre la fenolftaleína y el ion OH- si la velocidad instantánea de reacción es de 2,5 x 10-5 moles por litro por segundo cuando la concentración de fenolftaleína es de 0,0025 M.
Haga clic aquí para comprobar su respuesta al Problema de práctica 2.
Haga clic aquí para ver una solución al Problema de práctica 2.
Problema de práctica 3:
Utilice la constante de velocidad para la reacción entre la fenolftaleína y el ion OH- para calcular la velocidad instantánea inicial de reacción para los datos experimentales enumerados en la tabla anterior.
Haga clic aquí para comprobar su respuesta al Problema de Práctica 3.
Haga clic aquí para ver una solución al Problema de Práctica 3.
![]()
Diferentes formas de expresar la velocidad de reacción
Por lo general, hay más de una forma de medir la velocidad de una reacción. Podemos estudiar la descomposición del yoduro de hidrógeno, por ejemplo, midiendo la velocidad a la que se forma H2 o I2 en la siguiente reacción o la velocidad a la que se consume el HI.
2 HI(g) H2(g) + I2(g)
Experimentalmente encontramos que la velocidad a la que se forma I2 es proporcional al cuadrado de la concentración de HI en cualquier momento.
![]()
¿Qué ocurriría si estudiáramos la velocidad a la que se forma el H2? La ecuación equilibrada sugiere que el H2 y el I2 deben formarse exactamente a la misma velocidad.
![]()
¿Qué ocurriría, sin embargo, si estudiáramos la velocidad a la que se consume el HI en esta reacción? Como el HI se consume, el cambio en su concentración debe ser un número negativo. Por convención, la velocidad de una reacción siempre se reporta como un número positivo. Por lo tanto, tenemos que cambiar el signo antes de reportar la velocidad de reacción para un reactivo que se consume en la reacción.
![]()
El signo negativo hace dos cosas. Matemáticamente, convierte un cambio negativo en la concentración de HI en una tasa positiva. Físicamente, nos recuerda que la concentración del reactivo disminuye con el tiempo.
¿Cuál es la relación entre la velocidad de reacción obtenida al observar la formación de H2 o I2 y la velocidad obtenida al observar la desaparición del HI? La estequiometría de la reacción dice que se consumen dos moléculas de HI por cada molécula de H2 o I2 producida. Esto significa que la velocidad de descomposición del HI es dos veces más rápida que la velocidad a la que se forman el H2 y el I2. Podemos traducir esta relación en una ecuación matemática de la siguiente manera.
![]()
Como resultado, la constante de velocidad obtenida al estudiar la velocidad a la que se forman el H2 y el I2 en esta reacción (k) no es la misma que la constante de velocidad obtenida al controlar la velocidad a la que se consume el HI (k’)
Problema de práctica 4:
Calcule la velocidad a la que desaparece el HI en la siguiente reacción en el momento en que se forma el I2 a una velocidad de 1.8 x 10-6 moles por litro por segundo:
2 HI(g) ![]() H2(g) + I2(g)
H2(g) + I2(g)
Haga clic aquí para comprobar su respuesta al Problema de Práctica 4.
Haga clic aquí para ver una solución al Problema de Práctica 4.
![]()
La ley de la tasa frente a la estequiometría de una reacción
En la década de 1930, Sir Christopher Ingold y sus colaboradores de la Universidad deLondres estudiaron la cinética de reacciones de sustitución como la siguiente.
CH3Br(aq) + OH-(aq)
CH3OH(aq) + Br-(aq)
Encontraron que la velocidad de esta reacción es proporcional a lasconcentraciones de ambos reactantes.
Tasa = k(CH3Br)(OH-)
Cuando realizaron una reacción similar con un material de partida ligeramente diferente, obtuvieron productos similares.
(CH3)3CBr(aq) + OH-(aq)![]() (CH3)3COH(aq) + Br-(aq)
(CH3)3COH(aq) + Br-(aq)
Pero ahora la velocidad de reacción era proporcional a la concentración de sólo uno de los reactantes.
Rata = k((CH3)3CBr)
Estos resultados ilustran un punto importante: La ley de velocidad para una acción no puede predecirse a partir de la estequiometría de la reacción; debe determinarseexperimentalmente. A veces, la ley de velocidad es consistente con lo que esperamos de la estequiometría de la reacción.
2 HI(g) H2(g) + I2(g)
Rata = k(HI)2
A menudo, sin embargo, no lo es.
| 2 N2O5(g) |
Tasa = k(N2O5) |
![]()
Orden de Molecularidad
Algunas reacciones ocurren en un solo paso. La reacción en la que un átomo de cloro se transfiere de ClNO2 a NO para formar NO2 y ClNO es un buen ejemplo de una reacción de un solo paso.
ClNO2(g) + NO(g)
NO2(g) + ClNO(g)
Otras reacciones ocurren por una serie de pasos individuales. El N2O5, por ejemplo, se descompone en NO2 y O2 por un mecanismo de tres pasos.
| Paso 1: | N2O5 |
|
| Paso 2: | NO2 + NO3 |
|
| Paso 3: | NO + NO3 |
Los pasos de una reacción se clasifican en términos de molecularidad, que describe el número de moléculas consumidas. Cuando se consume una sola molécula, el paso se denomina unimolecular. Cuando se consumen dos moléculas, es bimolecular.
Problema de práctica 5:
Determine la molecularidad de cada paso en la reacción por la que el N2O5 se descompone en NO2 y O2.
Haga clic aquí para comprobar su respuesta al Problema de práctica 5.
Haga clic aquí para ver una solución al Problema de práctica 5.
Las reacciones también pueden clasificarse en términos de su orden. La descomposición del N2O5 es una reacción de primer orden porque la velocidad de reacción depende de la concentración de N2O5 elevada a la primera potencia.
Tasa = k(N2O5)
La descomposición del HI es una reacción de segundo orden porque la velocidad de reacción depende de la concentración de HI elevada a la segunda potencia.
Tasa = k(HI)2
Cuando la tasa de una reacción depende de más de un reactivo, clasificamos la reacción en términos del orden de cada reactivo.
Problema de práctica 6:
Clasifique el orden de la reacción entre NO y O2 para formar NO2:
2 NO(g) + O2(g) ![]() 2 NO2(g)
2 NO2(g)
Suponga la siguiente ley de velocidad para esta reacción:
Tasa = k(NO)2(O2)
Haga clic aquí para comprobar su respuesta al problema de práctica 6.
La diferencia entre la molecularidad y el orden de una reacción es importante. La molecularidad de una reacción, o un paso dentro de una reacción, describe lo que ocurre a nivel molecular. El orden de una reacción describe lo que ocurre a escala macroscópica. Determinamos el orden de una reacción observando cómo aparecen los productos de una reacción o cómo desaparecen los reactantes. La molecularidad de la reacción es algo que deducimos para explicar estos resultados experimentales.
![]()
Modelo de la teoría de colisiones de las reacciones químicas
El modelo de la teoría de colisiones de las reacciones químicas puede utilizarse para explicar las leyes de velocidad observadas tanto para las reacciones de un paso como para las de varios pasos. Este modelo supone que la velocidad de cualquier paso en una reacción depende de la frecuencia de las colisiones entre las partículas implicadas en ese paso.
La figura siguiente proporciona una base para entender las implicaciones del modelo de la teoría de colisiones para reacciones simples de un paso, como la siguiente.
ClNO2(g) + NO(g) ![]() NO2(g) + ClNO(g)
NO2(g) + ClNO(g)
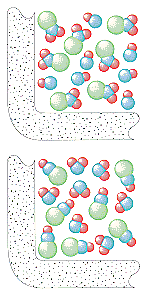
La teoría cinética molecular asume que el número de colisiones por segundo en un gas depende del número de partículas por litro. Por lo tanto, la velocidad a la que se forman el NO2 y el ClNO en esta reacción debería ser directamente proporcional a las concentraciones tanto del ClNO2 como del NO.
Tasa = k(ClNO2)(NO)
El modelo de la teoría de colisiones sugiere que la tasa de cualquier paso en una reacción es proporcional a las concentraciones de los reactivos consumidos en ese paso. Por lo tanto, la ley de velocidad para una reacción de un paso debería coincidir con la estequiometría de la misma.
La siguiente reacción, por ejemplo, ocurre en un solo paso.
CH3Br(aq) + OH-(aq) ![]() CH3OH(aq) + Br-(aq)
CH3OH(aq) + Br-(aq)
Cuando estas moléculas chocan en la orientación adecuada, un par de electrones no enlazantes en el ion OH- pueden ser donados al átomo de carbono en el centro de la molécula de CH3Br, como se muestra en la figura siguiente.
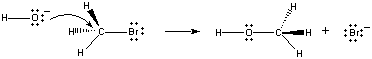
Cuando esto ocurre, se forma un enlace carbono-oxígeno al mismo tiempo que se rompe el enlace carbono-bromo. El resultado neto de esta reacción es la sustitución de un ionOH- por un ion Br -. Debido a que la reacción ocurre en un solo paso, que implica colisiones entre los dos reactantes, la velocidad de esta reacción esproporcional a la concentración de ambos reactantes.
Tasa = k(CH3Br)(OH-)
No todas las reacciones ocurren en un solo paso. La siguiente reacción ocurre en tres pasos, como se muestra en la figura siguiente.
(CH3)3CBr(aq) + OH-(aq)![]() (CH3)3COH(aq) + Br-(aq)
(CH3)3COH(aq) + Br-(aq)
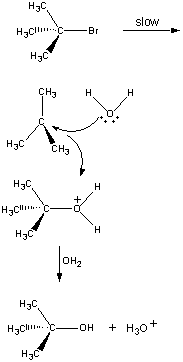
En el primer paso, la molécula de (CH3)3CBr se disocia en un par de iones.
| Primer paso | 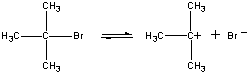 |
El ion (CH3)3C+ cargado positivamente reacciona entonces con el agua en un segundo paso.
| Segundo paso | 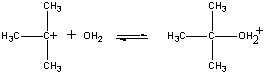 |
El producto de esta reacción pierde entonces un protón al ion OH o al agua en el último paso.
| Tercer paso | 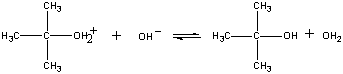 |
Los pasos segundo y tercero de esta reacción son mucho más rápidos que el primero.
| (CH3)3CBr |
Paso lento | |
| (CH3)3C+ + H2O |
Paso rápido | |
| (CH3)3COH2+ + OH- |
Paso rápido |
La velocidad global de la reacción es por tanto más o menos igual a la velocidad del primer paso. Por lo tanto, el primer paso se denomina paso limitador de la velocidad en esta reacción porque limita literalmente la velocidad a la que se pueden formar los productos de la reacción. Debido a que sólo un reactivo está involucrado en el paso limitante de la velocidad, la velocidad global de la reacción es proporcional a la concentración de sólo este reactivo.
Rata = k((CH3)3CBr)
La ley de velocidad para esta reacción, por lo tanto, difiere de lo que podríamos predecir a partir de la estequiometría de la reacción. Aunque la reacción consume tanto (CH3)3CB como OH-, la velocidad de la reacción sólo es proporcional a la concentración de (CH3)3CBr.
Las leyes de velocidad de las reacciones químicas pueden explicarse mediante las siguientes reglas generales.
La velocidad de cualquier paso de una reacción es directamente proporcional a las concentraciones de los reactivos consumidos en ese paso.
La ley de velocidad global de una reacción está determinada por la secuencia de pasos, o el mecanismo, por el que los reactivos se convierten en los productos de la reacción.
La ley de velocidad global de una reacción está dominada por la ley de velocidad del paso más lento de la reacción.