Análisis discriminante lineal, explicado

Clasificación por análisis discriminante

Veamos cómo se puede derivar el LDA como método de clasificación supervisado. Consideremos un problema de clasificación genérico: Una variable aleatoria X proviene de una de K clases, con algunas densidades de probabilidad específicas de la clase f(x). Una regla discriminante trata de dividir el espacio de datos en K regiones disjuntas que representan todas las clases (imagine las casillas de un tablero de ajedrez). Con estas regiones, la clasificación por análisis discriminante significa simplemente que asignamos x a la clase j si x está en la región j. La pregunta es entonces, ¿cómo sabemos en qué región caen los datos x? Naturalmente, podemos seguir dos reglas de asignación:

• Regla de máxima verosimilitud: Si asumimos que cada clase puede ocurrir con igual probabilidad, entonces asignamos x a la clase j si

• Regla bayesiana: Si conocemos las probabilidades a priori de la clase, π, entonces asignamos x a la clase j si

Análisis discriminante lineal y cuadrático

Si suponemos que los datos provienen de una distribución gaussiana multivariante, es decir.es decir, la distribución de X se puede caracterizar por su media (μ) y su covarianza (Σ), se pueden obtener formas explícitas de las reglas de asignación anteriores. Siguiendo la regla bayesiana, clasificamos los datos x en la clase j si tiene la mayor probabilidad entre todas las K clases para i = 1,…,K:

La función anterior se denomina función discriminante. Obsérvese el uso de la log-verosimilitud aquí. En otras palabras, la función discriminante nos dice qué probabilidad tienen los datos x de cada clase. Por tanto, la frontera de decisión que separa dos clases cualesquiera, k y l, es el conjunto de x en el que dos funciones discriminantes tienen el mismo valor. Por lo tanto, cualquier dato que caiga en la frontera de decisión es igualmente probable que provenga de las dos clases (no podríamos decidir).

LDA surge en el caso de que asumamos una covarianza igual entre K clases. Es decir, en lugar de una matriz de covarianza por clase, todas las clases tienen la misma matriz de covarianza. Entonces podemos obtener la siguiente función discriminante:

Nótese que se trata de una función lineal en x. Así, la frontera de decisión entre cualquier par de clases es también una función lineal en x, razón de su nombre: análisis discriminante lineal. Sin el supuesto de covarianza igual, el término cuadrático de la probabilidad no se cancela, por lo que la función discriminante resultante es una función cuadrática en x:

En este caso, el límite de decisión es cuadrático en x. Esto se conoce como análisis discriminante cuadrático (QDA).

¿Qué es mejor? ¿LDA o QDA?

En los problemas reales, los parámetros de la población suelen ser desconocidos y se estiman a partir de los datos de entrenamiento como las medias y las matrices de covarianza de la muestra. Mientras que QDA acomoda límites de decisión más flexibles en comparación con LDA, el número de parámetros necesarios para ser estimados también aumenta más rápido que el de LDA. Para LDA, se necesitan (p+1) parámetros para construir la función discriminante en (2). Para un problema con K clases, sólo necesitaríamos (K-1) de estas funciones discriminantes eligiendo arbitrariamente una clase como clase base (restando la probabilidad de la clase base de todas las demás clases). Por lo tanto, el número total de parámetros estimados para LDA es (K-1)(p+1).

Por otro lado, para cada función discriminante QDA en (3), es necesario estimar el vector de media, la matriz de covarianza y la clase previa:
– Media: p
– Covarianza: p(p+1)/2
– Prioridad de clase: 1
De forma similar, para QDA, necesitamos estimar (K-1){p(p+3)/2+1} parámetros.

Por lo tanto, el número de parámetros estimados en LDA aumenta linealmente con p mientras que el de QDA aumenta cuadráticamente con p. Esperaríamos que QDA tuviera peor rendimiento que LDA cuando la dimensión del problema es grande.

¿Lo mejor de dos mundos? Compromiso entre LDA & QDA

Podemos encontrar un compromiso entre LDA y QDA regularizando las matrices de covarianza de las clases individuales. La regularización significa que ponemos una cierta restricción en los parámetros estimados. En este caso, requerimos que la matriz de covarianza individual se reduzca hacia una matriz de covarianza común a través de un parámetro de penalización, por ejemplo, α:

La matriz de covarianza común también puede regularizarse hacia una matriz de identidad a través de un parámetro de penalización, por ejemplo β:

En situaciones en las que el número de variables de entrada supera en gran medida el número de muestras, la matriz de covarianza puede ser mal estimada. Es de esperar que la reducción mejore la estimación y la precisión de la clasificación. Esto se ilustra en la siguiente figura.

Cálculo para LDA

Podemos ver en (2) y (3) que los cálculos de las funciones discriminantes pueden simplificarse si diagonalizamos las matrices de covarianza primero. Es decir, los datos se transforman para tener una matriz de covarianza de identidad (sin correlación, varianza de 1). En el caso de LDA, así es como procedemos con el cálculo:

El paso 2 esferiza los datos para producir una matriz de covarianza de identidad en el espacio transformado. El paso 4 se obtiene siguiendo (2).

Tomemos un ejemplo de dos clases para ver qué hace realmente el LDA. Supongamos que hay dos clases, k y l. Clasificamos x en la clase k si

La condición anterior significa que es más probable que la clase k produzca datos x que la clase l. Siguiendo los cuatro pasos anteriores, escribimos

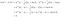
Es decir, clasificamos los datos x en la clase k si

La regla de asignación derivada revela el funcionamiento del LDA. El lado izquierdo (l.h.s.) de la ecuación es la longitud de la proyección ortogonal de x* sobre el segmento de línea que une las dos medias de clase. El lado derecho es la ubicación del centro del segmento corregido por las probabilidades previas de clase. Esencialmente, el LDA clasifica los datos esféricos a la media de la clase más cercana. Podemos hacer dos observaciones aquí:

1. El punto de decisión se desvía del punto medio cuando las probabilidades previas de clase no son las mismas, es decir, el límite se empuja hacia la clase con una probabilidad previa más pequeña.
2. Los datos se proyectan en el espacio abarcado por las medias de clase (la multiplicación de x* y la sustracción de la media en el h.l. de la regla). Las comparaciones de distancia se hacen entonces en ese espacio.